概念:有大小和方向的量
基础算法:
(1)加:\((A.x + B.x,A.y + B.y)\)
(2)减:\((A.x - B.x,A.y - B.y)\)
(3)乘常数:\((A.x * k,A.y * k)\)
(4)点积:\(A · B = |A||B|\cos\theta = A.x * B.x + A.y*B.y\)
(5)叉积:\(A \times B = |A||B|\sin\theta = A.x * B.y - A.y*B.x\)
(1)旋转:将 \((x,y)\) 逆时针旋转 \(\theta\) 就是 \((x * \cos\theta - y * \sin\theta,x * \sin\theta + y * \cos\theta)\)
(2)把向量 \(A\) 转到与向量 \(B\) 同向:\(B * \dfrac{|A|}{|B|}\)
(3)求多边形面积:\(\dfrac{1}{2}|\sum_{i=1}^{n-1}P_i \times P_{(i+1)\%n}|\)
(4)以 \(A\) 为原点 \(B\) 为单位点求 \(P\) 的新坐标:\((\vec{AB} · \vec{AP},\vec{AB} \times \vec{AP}) * \dfrac{1}{|AB|^2}\)
(5)\(P\) 与直线 \(AB\) 的位置关系:根据 \(\vec{AB} \times \vec{AP}\)
(6)点 \(P\) 在直线 \(AB\) 上的投影:\(A + \dfrac{\vec{AB} * (\vec{AB} · \vec{AP})}{|AB|^2}\)
(7)点与线段的位置关系:判断与线段所在直线的位置关系、点积判断在哪里
(8)\(AB \mathop{//} CD:\vec{AB} \times \vec{CD} = 0\)
(9)直线 \(AB\) 和直线 \(CD\) 求交点:\(A + \vec{AB} * \dfrac{\vec{CD}\times\vec{CA}}{\vec{AB} \times \vec{CD}}\)
(10)线段与直线求交点:线段两端点在直线两侧、直线求交点
求凸包:
(1)找到所有的点中最左下角的点,并加入栈中
(2)将所有点按极角排序逆时针
(3)每次找到一个点,判断该点是否在最后这条边的右边,若是则弹出栈顶,直到不能弹出就加入栈里
求下凸壳:
按横坐标从小到大排序,然后执行上文 (3)
求上凸壳:
按横坐标从大到小排序,然后执行上文(3)
本质:固定一个点,所求与另一个点的位置呈单峰函数且峰值关于固定点单调的算法
例题:题目描述:
求解凸多边形的直径。直径的定义为凸多边形上两点间距离的最大值。
解法:
(1)任意选择一个点为固定点
(2)以固定点在逆时针顺序下的下一个点为第二个点
(3)因为这两点间的距离与第二个点的位置呈单峰函数,且峰值关于固定点单调,所以就按逆时针方向移动第二个点
(4)移动到最大距离处,计算贡献,并按逆时针方向移动固定点,不移动第二个点
(5)重复(3)直到移动结束
例如下图所示:
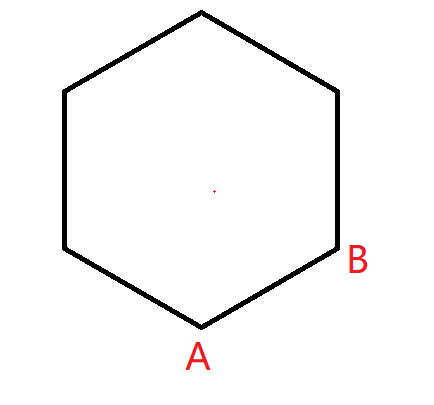
先随机找到固定点 \(A\),与对应的第二个点 \(B\)
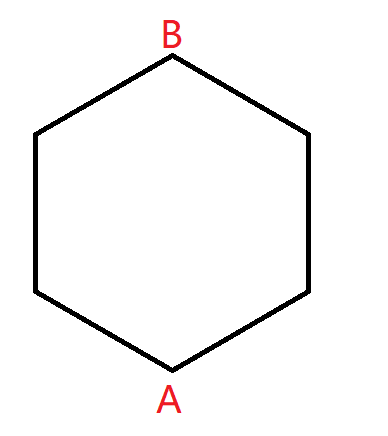
移动 \(B\) ,使得 \(A\) 与 \(B\) 两点间距离最大
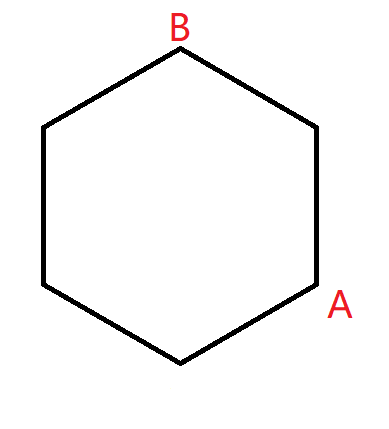
保持 \(B\) 不动,移动 \(A\)
然后再按照上文的方法一直循环执行
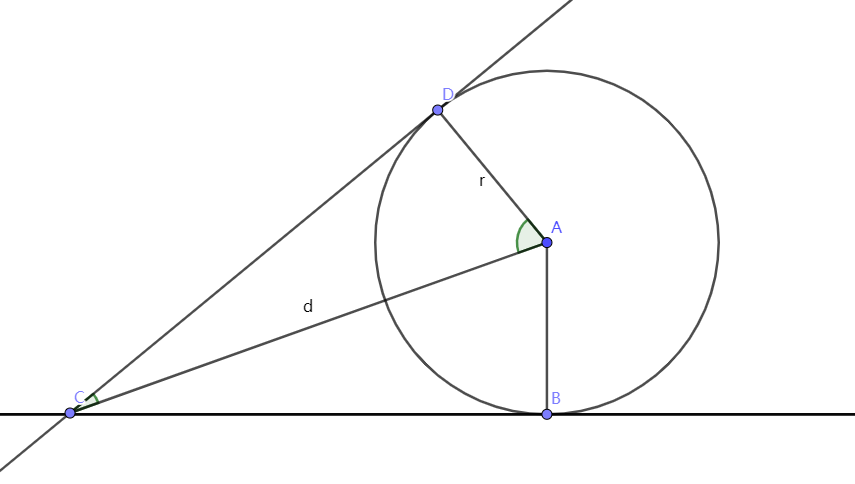
判断点是否在圆上: \(d \le r\)
\(d = |PC|,r = r\) \(\angle DAC = \arccos(\dfrac{r}{d}),\angle DAC = (\arcsin\dfrac{r}{d})\)
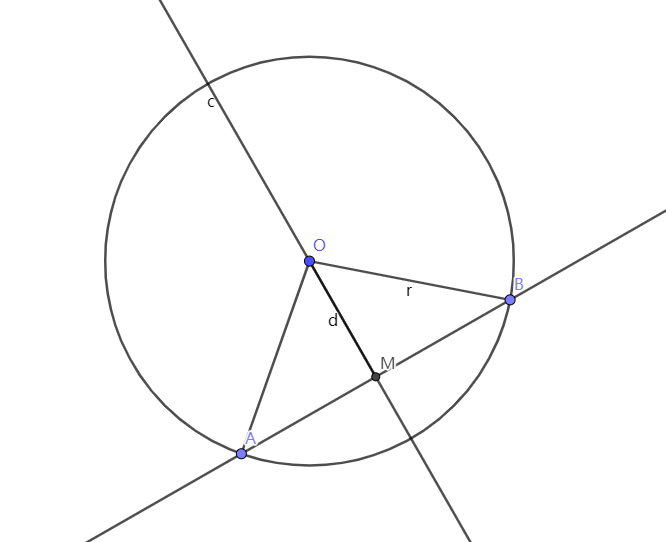
根据叉积得到 \(d\)
\(|MA| = |MB| = \sqrt{r^2 - d^2}\),\(\angle OBM = \arccos \dfrac{d}{r}\)
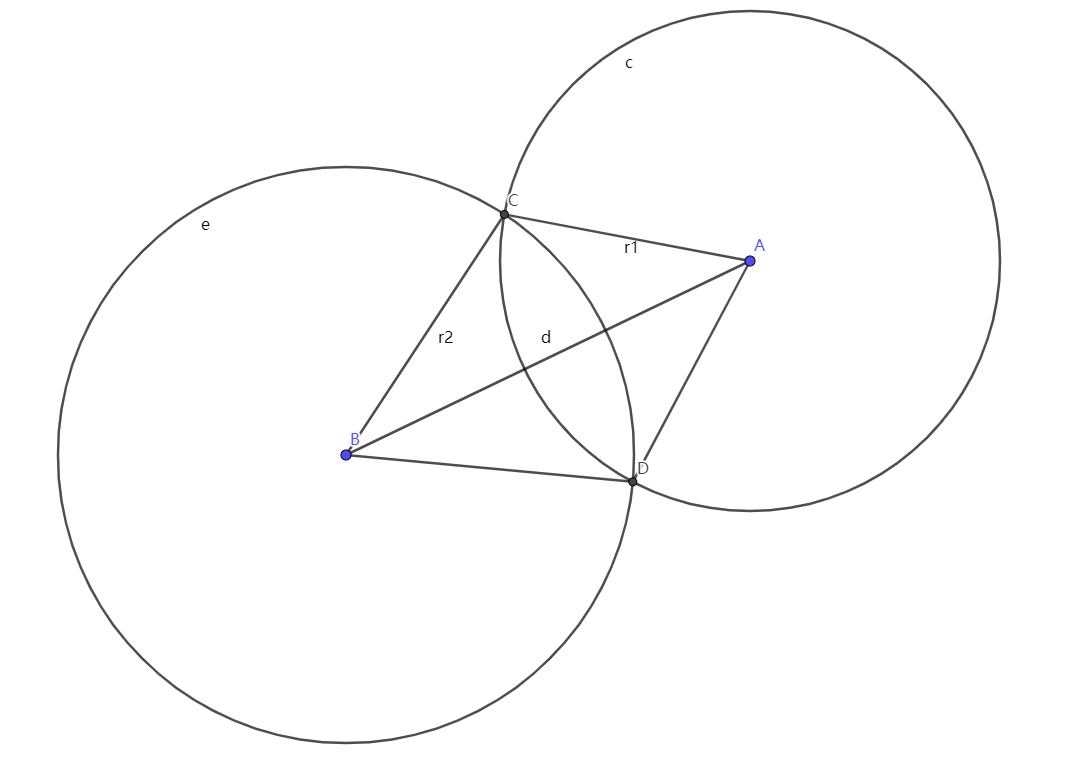
根据 \(d\) 与 \(r_1 + r_2\)

\(k = r_2 - r_1 , \angle CAB = \arccos \dfrac{r2-r1}{d},\angle DBA = \arccos \dfrac{r_1-r_2}{d}\)
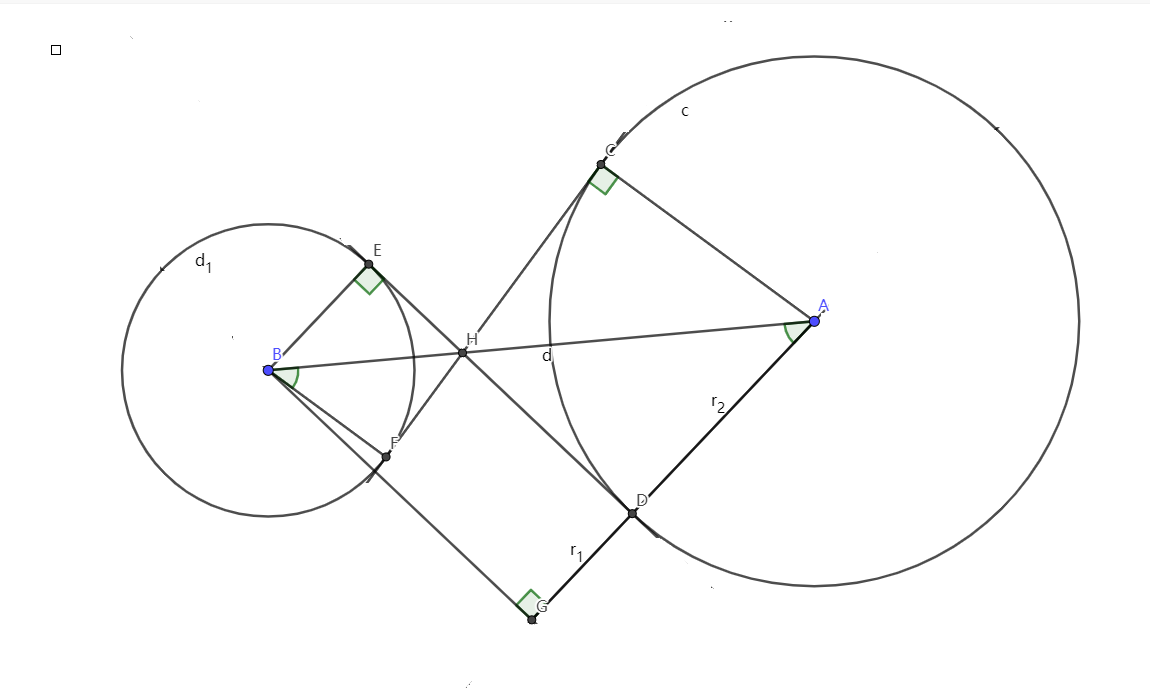
\(\angle BAG = \angle ABF = \arcsin \dfrac{r_1+r_2}{d}\)
