摘录总结于极客时间——《数据结构与算法之美》
我们学习数据结构与算法的目的就是为了让代码运行的更快、存储更节省空间。那么去了解代码的执行效率也是重要的一环。其实,只要涉及到的数据结构与算法,就一定离不开时间、空间复杂度的分析,而且,个人认为复杂度分析可以是数据结构与算法最精髓的一环了,只要掌握了它,那么数据结构与算法的内容就算是掌握了一半。
为什么有复杂度分析? 你可能觉得我把算法直接在我的机器上跑一边然后通过检测软件来实时获取结果就好,难道实打实的数据还不如我们的脑测吗?这是因为一段代码被放到另一台机器上运行时,我们得到的结果可能完全不一致,比如我先拿 i9 处理器处理数据,又拿 i3 处理器处理数据,这就会导致差异,并且如果测试数据的规模不一致也会导致数据多样。
所以,我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法。这就是我们今天要讲的时间、空间复杂度分析方法
算法的执行效率其实就是粗略的估算算法执行的时间,我们来观察下面的代码(代码非常简单,就是从 1,2,3.....n 的累加)
int cal() {
int sum = 0;
int i = 1;
for (; i <= n; i++) {
sum = sum + i;
}
return sum;
}
从 CPU 的角度来看这段代码,,基本都是读数据、运算、写数据。虽然每次 CPU 的执行个数、时间都不一致,但我们可以粗略的假设每段代码的运行时长是 unit_time。在这个基础上,这段代码的总执行时长是多少呢?
第 2、3 行代码分别需要 1 个 unit_time 的执行时间,第 4、5 行代码都执行了 n 遍,所以是 2nunit_time, 那么这段代码的总执行时长就是 (2+2n)unit_time。可以看出,所有的代码执行时间 T(n) 跟代码的执行次数有关。
接下来蹭热打铁,我们再来看一段实例代码:
int cal() {
int sum = 0;
int i = 1;
int j = 1;
for (; i <= n; i++) {
j = 1;
for (; j <= n; j++) {
sum = sum + j + i;
}
}
return sum;
}
第 1、2、3 行分别是 1 个 unit_time 的执行时间,第 4、5 行则是 2nunit_time 的执行时间,第 6、7 行是 2n²unit_time 的执行时间,那么得出的最后结果就是 T(n) = (3+2n+2n²)*unit_time 的执行时长。
是不是感觉有点领悟要领了?根据上面的案例,我们可以确认所有代码的执行时间T(n)与每行代码的执行次数n成正比:T(n)=O(f(n))
我来解释一下这段公式:
- T(n) 就是之前提到的表示代码执行的时间
- n 表示的是数据的规模
- f(n) 表示的是每次代码执行的综合,因为这是一个公式,所以用它来表示
- O 表示代码的执行时间 T(n) 与 f(n) 表达式成正比
所以第一个例子中 T(n)=O(2+2n),第二个例子就变成了 T(n)=O(3+2n+2n²),这就是大O时间复杂度表示法,怎么样是不是感觉还挺简单?
复杂度分析前面介绍了大O时间复杂度表示法的由来,那么如何去使用它呢?这里介绍三种较好的方式来套用
关注循环执行次数最多的一行代码上面提到大O时间复杂度表示法只是一种变化趋势,那么像是常量、低阶、系数这种通常会被忽略掉,我们只要关心一个最大阶的量级就可以了,为了便于理解,还是拿前面的代码分析:
int cal() {
int sum = 0;
int i = 1;
for (; i <= n; i++) {
sum = sum + i;
}
return sum;
}
这里第 2、3 行代码都是常量级的执行时间,执行次数最多的是循环 n 遍的第 4、5 行代码,所以这块需要重点分析。前面我们也讲过,这两行代码被执行了n次,所以总的时间复杂度就是O(n)。
加法法则:总复杂度等于量级最大的那段代码的复杂度再举一个案例,你可以继续分析代码:
int cal() {
int sum_1 = 0;
int p = 1;
for(; p < 100; p++) {
sum1 = sum1 + p;
}
int sum_2 = 0;
int q = 1;
for(; q < n; q++) {
sum_2 = sum_@ + q;
}
int sum_3 = 0;
int i = 1;
int j = 1;
for(; i < n; i++) {
j = 1;
for(; j < n; j++) {
sum_3 = sum_3 + i + j;
}
}
return sum_1 + sum_2 + sum_3;
}
这段代码分为 3 块,第一快 sum_1 循环了 100 次,但他还是常量级别的运行时长,这里声明一下,不管是 1000、10000 次,当其中 n 无限大的时候可以被忽略。 那第二段代码和第三段代码的时间复杂度是多少呢?答案是O(n)和O(n2),你应该能容易就分析出来,我就不啰嗦了。
综合这三段代码的时间复杂度,我们取其中最大的量级。所以,整段代码的时间复杂度就为O(n2)。也就是说: 总的时间复杂度就等于量级最大的那段代码的时间
复杂度。那我们将这个规律抽象成公式就是:如果T1(n)=O(f(n)), T2(n)=O(g(n));那么T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))).
乘法法则主要涉及到的是递归的情况,类似一下加法法则,你应该能够猜到公式是什么样的把?
如果T1(n)=O(f(n)), T2(n)=O(g(n));那么T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))
看代码:
int cal() {
int ret = 0;
int i = 1;
for(; i < n; i++) {
ret = ret + f(i);
}
}
int f(int n) {
int sum = 0;
int i = 1;
for(; i < n; i++) {
sum = sum + i;
}
return sum;
}
我们单独看cal()函数。假设f()只是一个普通的操作,那第4~ 6行的时间复杂度就是, T1(n) = O(n)。但f()函数本身不是一个简单的操作,它的时间复杂度是T2(n) =
O(n),所以,整个cal()函数的时间复杂度就是, T(n) = T1(n) * T2(n) = O(n*n) = O(n2)
刚才讲得这些你不用特意去记,需要的是你去做练习,只要多看案例,多分析,就能做到“无招胜有招”。
虽然代码千差万别,但是其实大部分都可以归类,这里稍微总结一下:
- 常数阶——O(1)
- 对数阶——O(logn)
- 线性阶——O(n)
- 线性对数阶——O(nlogn)
- 平方阶、立方阶....k次方阶——O(n^k)
- 指数阶——O(2^n)
- 阶乘阶——O(n!)
对于刚罗列的复杂度量级,我们可以粗略地分为两类, 多项式量级和非多项式量级。其中,非多项式量级只有两个: O(2n)和O(n!)。
当数据规模n越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。所以,非多项式时间复杂度的算法其实是非常低效的算法。因此,关于他们就不展开将,只讲常见的:
- O(1)
这里需要纠正上面的一个观点(上面只是方便你记忆,之后也提到了可以忽略),O(1)只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。比如下面有 3 行代码,它的时间复杂度也是O(1),而不是O(3)
int i = 1;
int j = 2;
int sum = 3;
- O(logn)、 O(nlogn)
对数阶很常见,同时也是最难分析的一种时间复杂度。通过一个例子来说明一下
i = 1;
while (i <= n) {
i = i * 2;
}
根据我们前面讲的复杂度分析方法,第三行代码是循环执行次数最多的,所以我们只要分析第三行就可以了。从代码中可以看出,变量i的值从1开始取,每循环一次就乘以2。当大于n时,循环结束。还记得我们高中学过的等比数列吗?实际上,变量i的取值就是一个等比:2^0、2^1、2^2.....2^x = n
所以,我们只要知道x值是多少,就知道这行代码执行的次数了。通过2x=n求解x这个问题我们想高中应该就学过了,我就不多说了。 x=log2n,所以,这段代码的时间复杂度就是O(log2n)。
那么变一变:
i = 1;
while (i <= n) {
i = i * 3;
}
顺理成章,这段代码的时间复杂度是 O(log3n),但是实际上不管以 2 为底、3 为底还是 10 为底也好,我们可以把所有对数阶的时间复杂度都记为O(logn)。为什么呢?
我们都知道对数可以互相转换, log3n就等于log32 * log2n,所以O(log3n) = O(C * log2n),其中C=log32是一个常量。基于我们前面的一个理论: 在采用
大O标记复杂度的时候,可以忽略系数,即O(Cf(n)) = O(f(n))。所以, O(log2n) 就等于O(log3n)。因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为O(logn)
那么 O(nlogn) 也就很好理解了,一段代码的执行效率是 O(logn),它被放到了一个循环内被执行了 n 次。
- O(m+n)、 O(m*n)
我们再来讲一种跟前面都不一样的时间复杂度,代码的复杂度由两个数据的规模来决定。老规矩,先看代码!
int cal(int m, int n) {
int sum_1 = 0;
int i = 1;
for (; i < m; ++i) {
sum_1 = sum_1 + i;
}
int sum_2 = 0;
int j = 1;
for (; j < n; ++j) {
sum_2 = sum_2 + j;
}
return sum_1 + sum_2;
}
从代码中可以看出, m和n是表示两个数据规模。我们无法事先评估m和n谁的量级大,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是O(m+n)。
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为: T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效: T1(m)*T2(n) = O(f(m) * f(n))
我们还需要继续了解最好、最坏、平均三种复杂度分析方面的知识,再掌握这几个概念后,那对于你来说,复杂度分析这部分内容就没什么大问题了(但其实只有只有同一块代码在不同的情况下,时间复杂度有量级的差距,我们才会使用这三种复杂度表示法来区分)。
看到代码:
// n 表示数组的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x)
pos = i;
}
return pos;
}
应该可以看出来,这代码的主要功能就是在一个数组内查找变量 x 出现的位置,如果找到就返回坐标,没有找到就返回 -1。按照上面的分析法,这段代码的时间负责度就是 O(n)。
但其实我们查询数据的时候往往都是找到后直接退出循环,而不是特地的再继续遍历循环,直到循环结束,也就是说这样:
// n 表示数组的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
那么问题来了,这样方式代码的时间复杂度还是 O(n) 吗?你想,要查询的变量可能就在数组的第一位,那么就不需要再继续遍历剩下的数组,时间复杂度就是 O(1);如果又是在数组的最后一位,那么时间复杂度就是 O(n)。所以,不同的情况下,这段代码的时间复杂度是不一样的。
为了理清这种情况,我们引入最好、最坏、平均时间复杂度。
平均时间复杂度又该怎么分析呢?我还是借助刚才查找变量x的例子来给你解释。要查找的变量x在数组中的位置,有n+1种情况: 在数组的0~ n-1位置中和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来,然后再除以n+1,就可以得到需要遍历的元素个数的平均值,即:
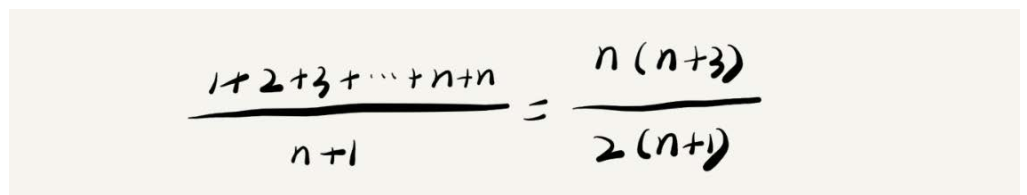
我们知道,时间复杂度的大O标记法中,可以省略掉系数、低阶、常量,所以,咱们把刚刚这个公式简化之后,得到的平均时间复杂度就是O(n)。
推算结果虽然是正确的,但是计算过程还是有些问题。我们知道,要查找的变量x,要么在数组里,要么就不在数组里。这两种情况对应的概率统计起来很麻烦,为了方便你理解,我们假设在数组中与不在数组中的概率都为1/2。另外,要查找的数据出现在0~ n-1这n个位置的概率也是一样的,为1/n。所以,根据概率乘法法则,要查找的数据出现在0~ n-1中任意位置的概率就是1/(2n)。
因此,前面的推导过程中存在的最大问题就是,没有将各种情况发生的概率考虑进去。如果我们把每种情况发生的概率也考虑进去,那平均时间复杂度的计算过程就变成了这样:
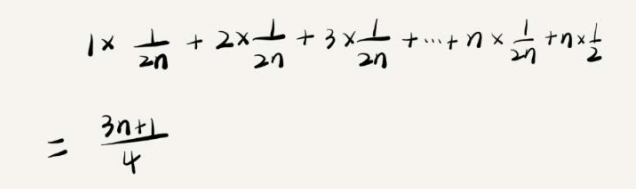
这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。但是去掉系数和常量,结果还是 O(n)
这可能比之前的要复杂一些,但是就像前面说的,大部分情况下我们不需要分最好、最坏和平均。
