python观察日志(part3)--绘制科赫雪花图

学习笔记
理论部分：​分形与混沌

---

科赫雪花图

分形（fractal）是一种不同于欧氏几何学中元素的几何图形，科赫曲线就是一个分形.

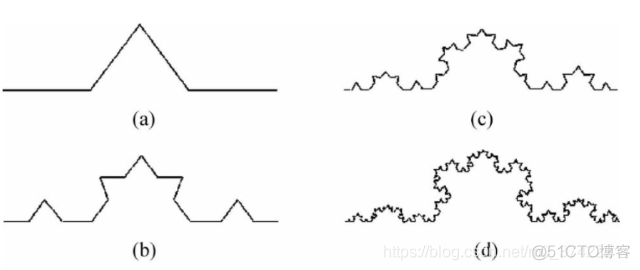
如上图所示，科赫曲线可以用如下方法产生：

在一段直线中间，以边长为的等边三角形的两边，去代替原来直线中间的，得到(a);

对(a)的每条线段重复上述做法又得到曲线(b) ;

对曲线(b) 的每段又重复，如此无穷地继续下去得到的极限曲线就是科赫曲线。

科赫雪花则是以等边三角形三边生成的科赫曲线组成的：

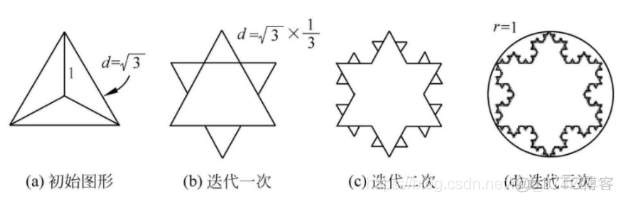
python实现

要绘制一个长度为x的科赫曲线，我们只需要：

绘制长度为x/3的科赫曲线

向左转60度

绘制长度为x/3的科赫曲线

向右转120度

绘制长度为x/3的科赫曲线

向左转60度

绘制长度为x/3的科赫曲线

大家有没有感觉，这个科赫曲线的产生过程有点类似于上面介绍的曲线(b)的产生过程？

这一点也比较好解释，我们可以通过分形的特征去理解。

分形有如下几个特征：

分形具有自相似性。分形自身可以看成是由许多与自己相似的、大小不一的部分组成。

分形具有无穷多的层次。无论在分形的哪个层次，总能看到有更精细的、下一个层次存在。分形图形有无限细节，可以不断放大，永远都有结构。

分形的维数可以是一个分数。

分形通常可以由一个简单的递归、迭代的方法产生出来。

python代码：

# -*- coding: utf-8 -*-
from __future__ import print_function, division

import turtle


def koch(t, n):
"""Draws a koch curve with length n."""
if n < 10:
t.fd(n)
return
m = n/3
koch(t, m)
t.lt(60)
koch(t, m)
t.rt(120)
koch(t, m)
t.lt(60)
koch(t, m)


def snowflake(t, n):
"""Draws a snowflake (a triangle with a Koch curve for each side)."""
for i in range(3):
koch(t, n)
t.rt(120)


bob = turtle.Turtle()

bob.pu()
bob.goto(-150, 90)
bob.pd()
snowflake(bob, 300)

turtle.mainloop()

实现过程：

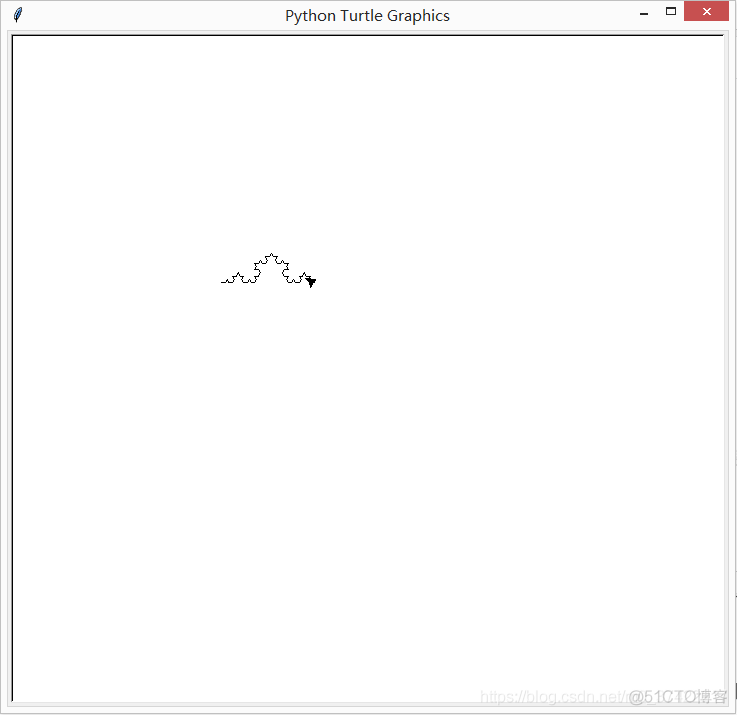
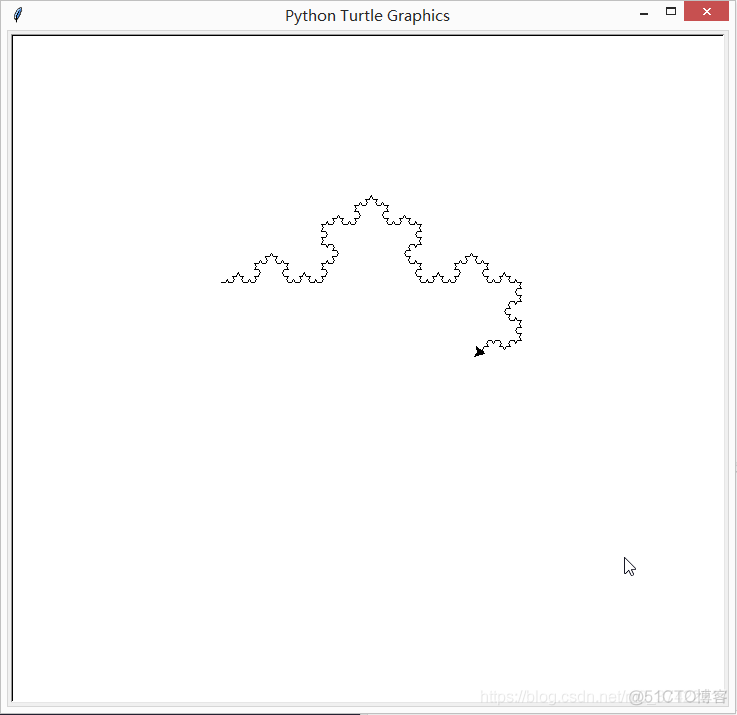
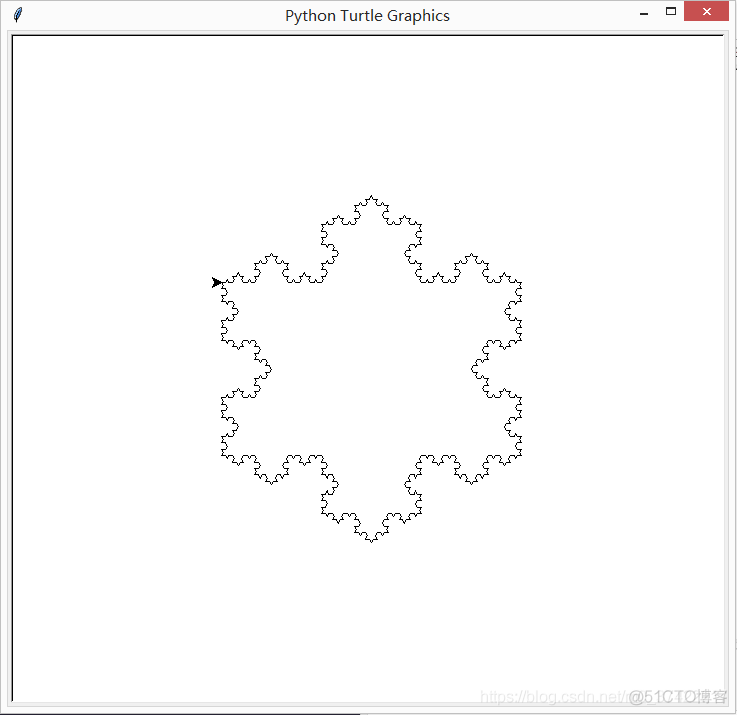
科赫雪花图绘制成功啦！