本文主要介绍遗传算法(实数编码)的交叉操作中的SBX,模拟二进制交叉。
首先,给出个人用python2.7实现的代码,具体模块已上传到:
https://github.com/guojun007/sbx_cross
1 #!/usr/bin/env python2 #encoding:UTF-8
3 import numpy as np
4 import random
5
6 """
7 SBX 模拟二进制交叉
8
9 输入:
10 population 种群矩阵
11 alfa 交叉概率
12 numRangeList 决策变量的上限(下限默认为0)
13 mu SBX方式的分布指数, 推荐为1
14 """
15 def cross(population, alfa, numRangeList, mu=1):
16 N=population.shape[0]
17 V=population.shape[1]
18 populationList=range(N)
19
20 for _ in xrange(N):
21 r=random.random()
22
23 if r<alfa:
24 p1, p2=random.sample(populationList, 2)
25 bq=np.array([0]*V)
26 randList=np.random.random(V)
27 #根据概率向量判断不同概率函数的选择
28 orTF=(randList<=0.5)
29
30 #计算不同决策变量的 不同概率选择 下的 系数
31 for j in xrange(V):
32 if orTF[j]==True:
33 bq[j]=(2.0*randList[j])**(1.0/(mu+1))
34 else:
35 bq[j]=(1.0/(2.0*(1-randList[j])))**(1.0/(mu+1))
36
37 #取出选定的两个个体
38 old_p1=population[p1, ]
39 old_p2=population[p2, ]
40 #计算交叉后的两个新个体
41 new_p1=0.5*((1+bq)*old_p1+(1-bq)*old_p2)
42 new_p2=0.5*((1-bq)*old_p1+(1+bq)*old_p2)
43
44 #上下限判断,防止越界
45 new_p1=np.max(np.vstack((new_p1, np.array([0]*V))), 0)
46 new_p1=np.min(np.vstack((new_p1, numRangeList)), 0)
47
48 new_p2=np.max(np.vstack((new_p2, np.array([0]*V))), 0)
49 new_p2=np.min(np.vstack((new_p2, numRangeList)), 0)
50
51 #将交叉后的个体更新回种群
52 population[p1, ]=new_p1
53 population[p1, ]=new_p2
54
55
56 ###以下是测试用例
57 if __name__=="__main__":
58 random.seed(0)
59 np.random.seed(0)
60 xN=20
61 yN=3
62 alfa=0.9
63 population=np.random.rand(xN*yN).reshape(xN, yN)*1.0
64
65 ###运行函数
66 print population
67 print '-'*50
68 cross(population, alfa, np.array([1]*3))
69 print '-'*50
70 print population



以下内容引至:
最近在做作业遇到一个Dejong’s fifth function的multi modal的问题,用传统的GA方法尝试了很多次,的确没办法搞定,随机很多次也不一定在global optimum的地方得到一次解。前几天去导师家里的路上谈到这个事情,导师说一般现在都用SBX和polynomial的mutation。于是回来找了相关论文来看,找到了SBX最早的论文,奇怪的是,在论文中竟然没有给出伪代码,只是在讲解他的motivation。大概的motivation是这样的:
1:SBX主要是用于real number的编码问题,但是借鉴与来自binary 编码的idea。在binary中,假设2个parent分别为p1和p2,后代分别为c1和c2。那么是这么一个属性的:(p1+p2)/2=(c1+c2)/2。再定义一个叫做spread factor的玩意β=|(c2−c1)/(p2−p1)|
2:在SBX中就要满足第一个属性,以及尽量β也binary中的概率分布一致。由此一个方案:
c1=(p2+p1)−0.5∗β(p2−p1)
c2=(p2+p1)+0.5∗β(p2−p1)
大家可以自己计算,是满足上面2个玩意的。
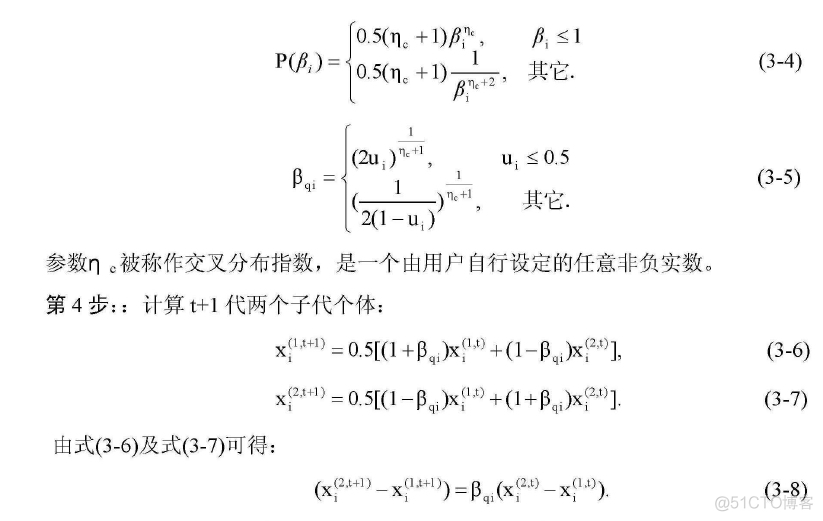
3:那么接下来其实就是求β的,因为是要让在real的问题中的β的分布尽量接近binary中的,那么就要首先知道binary中的分布。binary中的分布如下:
c(β)=0.5(n+1)βn,β≤1 and c(β)=0.5(n+1)1βn+2,β>1
也就是说β有2个分布的,具体怎么做呢?我看到有人实现是这么来的。
3.1:随机一个数字在[0,1]之间,如果该数字小于等于0.5按照第一个来求,否则按照第二个来求。求解的时候是按照对β的概率分布等于这个随机数字来计算的。这个只需要求积分即可,手工就能推导出来。
最后我用这个方法再加上tournament selection以及polynomial mutation的方法,在求解上面说的multi modal的问题的时候,竟然很多次都求解出来了!
