1 简介 针对麻雀搜索算法收敛速度缓慢,寻优精度不足和容易陷入局部最优等缺点,提出了一种融合正弦搜索策略和多样性变异处理策略的改进麻雀搜索算法.通过引入正弦搜索策略,自适应
1 简介
针对麻雀搜索算法收敛速度缓慢,寻优精度不足和容易陷入局部最优等缺点,提出了一种融合正弦搜索策略和多样性变异处理策略的改进麻雀搜索算法.通过引入正弦搜索策略,自适应调整个体权重提高算法收敛速度;针对个体聚集程度过高问题,采用多样性变异处理,引入生物学中种群聚集度的概念和柯西变异对最优解进行扰动,提高算法逃离局部最优的可能.通过九个不同特征的基准函数进行寻优测试,测试结果表明改进算法能够更快地收敛于最优值,有更好的平均值和标准差,表明了其具备更优的收敛速度,收敛稳定性和逃离局部最优值的能力.
2 部分代码
%_________________________________________________________________________%% 原始麻雀优化算法SSA %
%_________________________________________________________________________%
function [Best_pos,Best_score,curve]=SSA(pop,Max_iter,lb,ub,dim,fobj)
ST = 0.6; % 预警值
PD = 0.7; % 发现者的比列,剩下的是加入者
SD = 0.2; % 意识到有危险麻雀的比重
PDNumber = round(pop*PD); % 发现者数量
SDNumber = round(pop*SD); % 意识到有危险麻雀数量
if(max(size(ub)) == 1)
ub = ub.*ones(1,dim);
lb = lb.*ones(1,dim);
end
% 种群初始化
X0=initialization(pop,dim,ub,lb);
X = X0;
% 计算初始适应度值
fitness = zeros(1,pop);
for i = 1:pop
fitness(i) = fobj(X(i,:));
end
[fitness, index]= sort(fitness); % 排序
BestF = fitness(1);
WorstF = fitness(end);
GBestF = fitness(1); % 全局最优适应度值
for i = 1:pop
X(i,:) = X0(index(i),:);
end
curve=zeros(1,Max_iter);
GBestX = X(1,:); % 全局最优位置
X_new = X;
for i = 1: Max_iter
BestF = fitness(1);
WorstF = fitness(end);
R2 = rand(1);
for j = 1:PDNumber
if(R2<ST)
X_new(j,:) = X(j,:).*exp(-j/(rand(1)*Max_iter));
else
X_new(j,:) = X(j,:) + randn()*ones(1,dim);
end
end
for j = PDNumber+1:pop
% if(j>(pop/2))
if(j>(pop - PDNumber)/2 + PDNumber)
X_new(j,:)= randn().*exp((X(end,:) - X(j,:))/j^2);
else
% 产生-1,1的随机数
A = ones(1,dim);
for a = 1:dim
if(rand()>0.5)
A(a) = -1;
end
end
AA = A'*inv(A*A');
X_new(j,:)= X(1,:) + abs(X(j,:) - X(1,:)).*AA';
end
end
Temp = randperm(pop);
SDchooseIndex = Temp(1:SDNumber);
for j = 1:SDNumber
if(fitness(SDchooseIndex(j))>BestF)
X_new(SDchooseIndex(j),:) = X(1,:) + randn().*abs(X(SDchooseIndex(j),:) - X(1,:));
elseif(fitness(SDchooseIndex(j))== BestF)
K = 2*rand() -1;
X_new(SDchooseIndex(j),:) = X(SDchooseIndex(j),:) + K.*(abs( X(SDchooseIndex(j),:) - X(end,:))./(fitness(SDchooseIndex(j)) - fitness(end) + 10^-8));
end
end
% 边界控制
for j = 1:pop
for a = 1: dim
if(X_new(j,a)>ub(a))
X_new(j,a) =ub(a);
end
if(X_new(j,a)<lb(a))
X_new(j,a) =lb(a);
end
end
end
% 更新位置
for j=1:pop
fitness_new(j) = fobj(X_new(j,:));
end
for j = 1:pop
if(fitness_new(j) < GBestF)
GBestF = fitness_new(j);
GBestX = X_new(j,:);
end
end
X = X_new;
fitness = fitness_new;
% 排序更新
[fitness, index]= sort(fitness); % 排序
BestF = fitness(1);
WorstF = fitness(end);
for j = 1:pop
X(j,:) = X(index(j),:);
end
curve(i) = GBestF;
end
Best_pos =GBestX;
Best_score = curve(end);
end
3 仿真结果
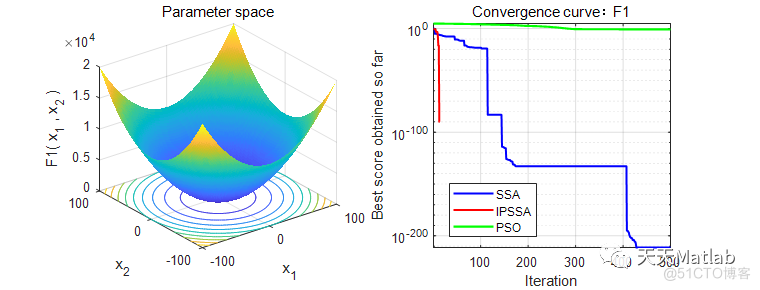

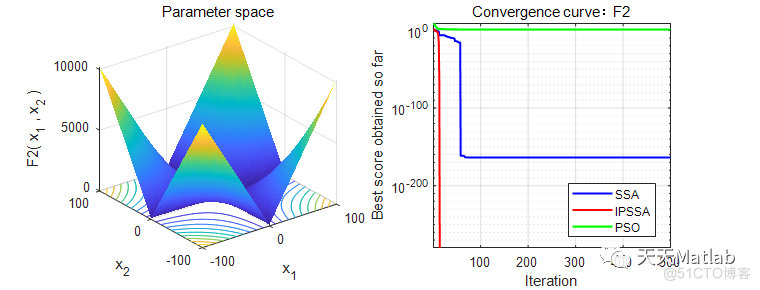

4 参考文献
[1]付华, 刘昊. 多策略融合的改进麻雀搜索算法及其应用[J]. 控制与决策, 2022, 37(1):10.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。


