1 简介 最近已经开发了几种元启发式优化算法来解决现实世界的问题。本文提出了一种新的元启发式算法,称为亨利气体溶解度优化 (HGSO),它模仿亨利定律支配的行为来解决具有挑战性
1 简介
最近已经开发了几种元启发式优化算法来解决现实世界的问题。本文提出了一种新的元启发式算法,称为亨利气体溶解度优化 (HGSO),它模仿亨利定律支配的行为来解决具有挑战性的优化问题。亨利定律是一个基本的气体定律,它与在固定温度下溶解到给定类型和体积的液体的给定气体的量有关。 HGSO 算法通过模仿气体的聚集行为来平衡搜索空间中的开发和探索,避免局部最优。
2 部分代码
%---------------------------------------------------------------------%% Henry Gas Solubility Optimization (HGSO) %
%---------------------------------------------------------------------%
%---输入------------------------------ ---------------
% 壮举:特征
% 标签:标签
% N : 气体数量
% max_Iter : 最大迭代次数
% num_clus : 气体类型的数量
% K : 常数
% alpha : 其他气体的影响
% beta : 常数
% L1 : 初始参数
% L2 : 初始参数
% L3 : 初始参数
%---输出------------------------------ --------------
% sFeat : 选定的功能
% Sf : 选定的特征索引
% Nf : 所选特征的数量
% 曲线:收敛曲线
%---------------------------------------------------------------------
%% 亨利气体溶解度优化
clc, clear, close;
% 基准数据集
load ionosphere.mat;
% 设置 20% 的数据作为验证集
ho = 0.2;
% 保持方法
HO = cvpartition(label,'HoldOut',ho);
% 参数设置
N = 20;
max_Iter = 200;
num_clus = 2; % 气体类型数/簇
K = 1; % 持续的
alpha = 1; % 其他气体的影响
beta = 1; % 持续的
L1 = 5E-3;
L2 = 100;
L3 = 1E-2;
% 亨利气体溶解度优化
[sFeat,Sf,Nf,curve] = jHGSO(feat,label,N,max_Iter,num_clus,K,alpha,beta,L1,L2,L3,HO);
% Plot convergence curve
plot(1:max_Iter,curve);
xlabel('迭代次数');
ylabel('适应度值');
title('HGSO'); grid on;
3 仿真结果
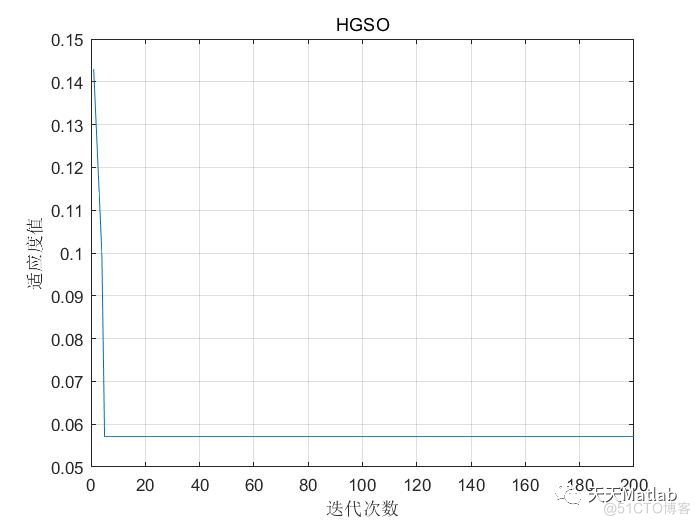

4 参考文献
Hashim, Fatma A., Essam H. Houssein, Mai S. Mabrouk, Walid Al-Atabany, and Seyedali Mirjalili. "Henry gas solubility optimization: A novel physics-based algorithm." Future Generation Computer Systems (2019).
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。


