❤️实现、冲突和散列函数❤️ 算法图解：第六章：广度优先搜索

Hello，大家好我叫是Dream呀，一个有趣的Python博主，小白一枚，多多关照 ?

入门须知：这片乐园从不缺乏天才，努力才是你的最终入场券！

最后，愿我们都能在看不到的地方闪闪发光，一起加油进步

“一万次悲伤，依然会有Dream，我一直在最温暖的地方等你”，唱的就是我！哈哈哈~

第六章：广度优先搜索

• ​​6.1图简介​​
• ​​6.2图是什么​​
• ​​6.3广度优先搜索​​

• ​​6.3.1查找最短路径​​
• ​​6.3.2队列​​

• ​​6.4实现图​​
• ​​6.5实现算法​​

• ​​6.5.1运行时间​​
• ​​6.5.2树​​

• ​​6.6小结​​
• ​​二级目录​​
• ​​三级目录​​
• ​​最后的福利​​

6.1图简介

图算法：广度优先搜索！

前往某一地点，需要的最短路径被称为是：最短路径问题

解决最短路径问题的算法被称作：广度优先搜索

6.2图是什么

图模拟一组连接。图由节点和边组成。

一个节点可以与众多个节点直接相连，这些节点被称为邻居。

6.3广度优先搜索

广度优先搜索是一种用于图的查找算法，可帮助回答两类问题：

第一类问题：从节点A出发，有前往B节点的路径吗？

第二类问题：从节点A出发，前往节点B的哪条路径最短呢？

拿卖水果的例子来说，如果你的朋友不是经销商的话，就将你的朋友也加入到名单中。这意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网，知道找到水果经销商。这就是广度优先搜索算法。

6.3.1查找最短路径

首先，拿上文来说，你应该先在一度关系中搜索，确定其没有芒果销售商后，才在二度关系中搜索。

有一个可实现这种目的的数据结构，那就是队列。

6.3.2队列

队列的工作原理和现实生活中的队列完全相同。如果你排在他前面，你将先上车。队列类似于栈，你不能随机地访问队列的元素。

队列只支持两种操作：入队和出队

队列先进先出，而栈后进先出！

6.4实现图

图由多个节点组成，每个节点都与邻近节点相连。

散列表让你能够将键映射到值，在这里只需要将节点映射到其所有邻居。散列表是无序的，因此添加键值对的顺序无关紧要！

关系单向：有向图

无向图没有箭头，直接相连的节点互为邻居。

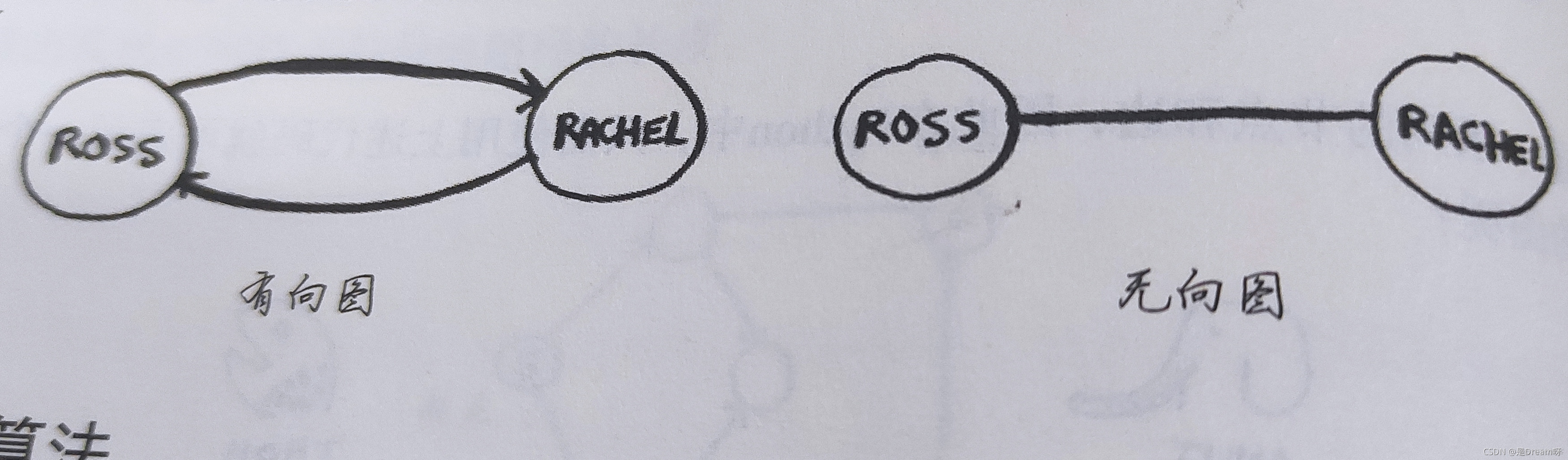
6.5实现算法

首先，创建一个队列。在Python中，可使用函数deque来创建一个双端队列。

from collections import deque
search_queue=deque()
search_queue+=graph["you"]

别忘了，这里的graph[‘you’]是一个数组，其中包含了你的所有邻居，如[‘alice’,‘bob’,‘claire’]。这些邻居都将加入到搜索队列里。

while search_queue:
person=search_queue.popleft()
if person_is_seller(person):
print(person + 'is seller')
return True
else:
search_queue+=graph[person]
return False

最后你还需要编写函数来判断一个人是不是经销商，如下所示：

def person_is_seller(name):
return name[-1]=='m'

检测这个人的名字是否以m结尾：如果是，他就是经销商。这种方法有点搞笑，但就这个实例而言是可行的。

这个算法将不断执行，直到满足以下条件之一：

1.找到一位经销商

2.队列为空，这将意味着你的人际关系网中没有经销商。

A既是B的朋友，又是C的朋友，因此他会两次被加入到队列中，这就会导致后手检测的将变成无用功。

from collections import deque
def search(name):
search_queue =deque()
search_queue+=graph[name]
searched=[]#这个数组用于记录检查过的人
while search_queue:
person = search_queue.popleft()
if person not in searched:#仅当这个人没检查过时才检查
if person_is_seller(person):
print(person+'is seller')
return True
else:
search_queue+=graph[person]
searched.append(person)#将这个人标记为检查过
return False
search("you")

6.5.1运行时间

如果你的整个人际关系网中搜索芒果销售商，就意味着你将沿着每条边前行，因此运行时间至少O（边数）

你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，即为O（1），因此对每个人都这样做需要的总时间为O（人数）。所以，广度优先搜索的运行时间为O（人数加边数），通常记作O（V+E），其中V为顶点数，E为边数。

6.5.2树

有一种图由节点和边组成，但没有往上指的箭头，这种图被称为树，树是一种特殊的图！

6.6小结

1.广度优先搜索指出是否有从A到B的路径；

2.如果有，广度优先搜索将找出最短路径；

3.面临类似于寻找最短路径的问题时，可以尝试使用图来建立模型，再使用广度优先搜索来解决问题；

4.有向图的边为箭头，箭头的方向指定了关系的方向；

5.无向图的边不带箭头，其中关系是双向的。

6.队列是先进先出的；

7.栈是后进先出的

8.你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必须是队列。

9.对于检查过的人，务必不要再去检查，否则可能导致无限循环。

二级目录

三级目录

最后的福利

☀️☀️☀️最后一点小福利带给大家：如果想快速上手python的小伙伴们，这个详细整理PPT可以迅速帮助大家打牢python基础，需要的小伙伴们可以下载一下 Python入门基础教程全套+小白速成+学不会来找我！

还有自制表白神器，需要自取：

Python表白神器，源码+解析+各种完美配置+浪漫新颖

好啦，这就是今天要给大家分享的全部内容了

如果你喜欢的话，就不要吝惜你的一键三连了~