Hello,大家好我叫是Dream呀,一个有趣的Python博主,小白一枚,多多关照 入门须知:这片乐园从不缺乏天才,努力才是你的最终入场券! ?最后,愿我们都能在看不到的地

Hello,大家好我叫是Dream呀,一个有趣的Python博主,小白一枚,多多关照
入门须知:这片乐园从不缺乏天才,努力才是你的最终入场券! ?最后,愿我们都能在看不到的地方闪闪发光,一起加油进步
“一万次悲伤,依然会有Dream,我一直在最温暖的地方等你”,唱的就是我!哈哈哈
第2章 内积空间
- 一、内积空间
- 二、 向量的度量
- 三、向量的正交化方法
- 1. 正交的概念
- 2. 正交向量组的概念
- 3.标准正交向量组(标准正交组)
- 4. 正交向量组a1 , , ,an 线性无关
- 5. 正交基
- 6. 标准正交基(规范正交基)
- 7. 若e1,... en 是内积空间V 的一个基,且e1,... en是标准正交向量组,则称e1,... en 是内积空间V的一个标准正交基
- 7. 求标准正交向量组的方法(施密特正交化方法)
- 8、正交矩阵
- 四、度量矩阵及性质
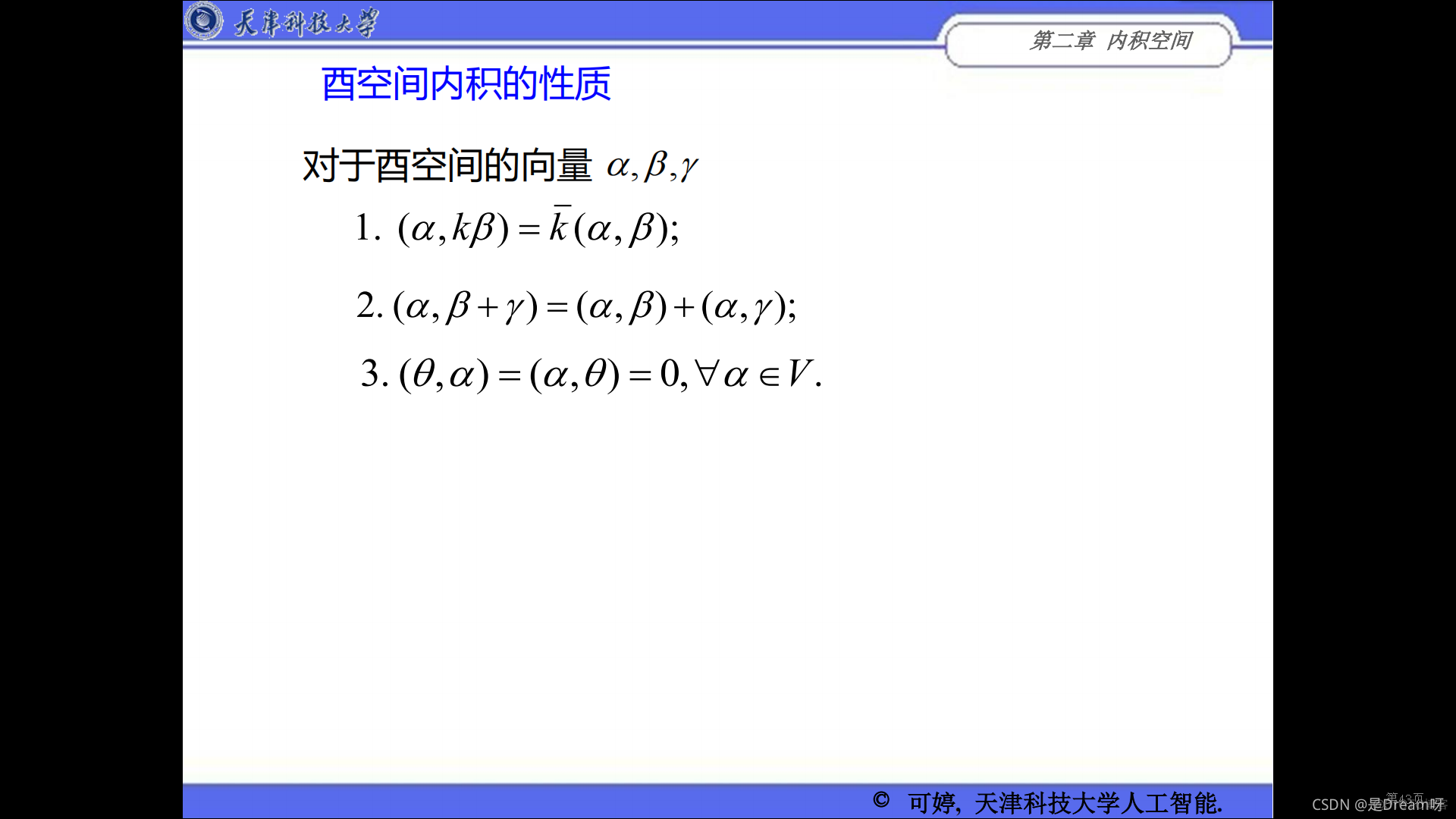
- 五、酉空间
- 6.1 支持向量分类机
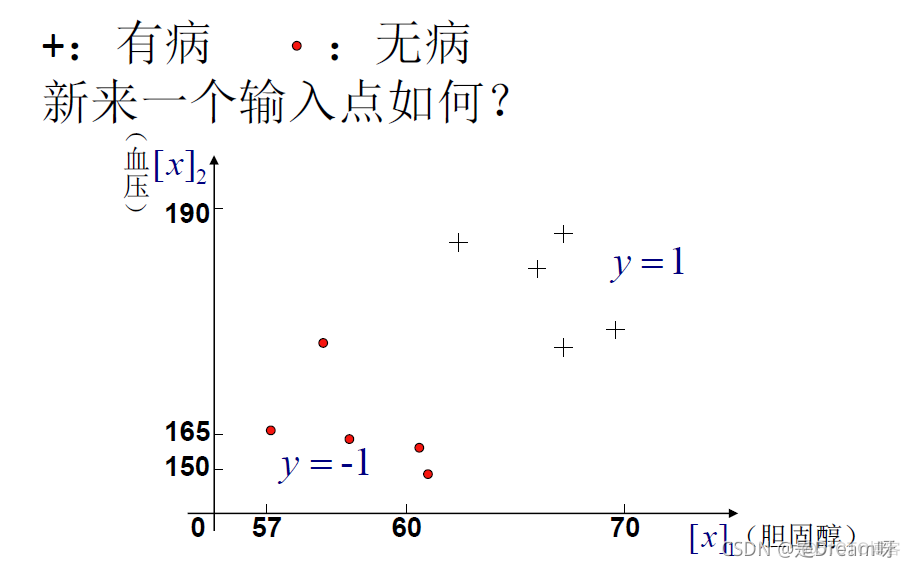
- 1、引例:心脏病诊断
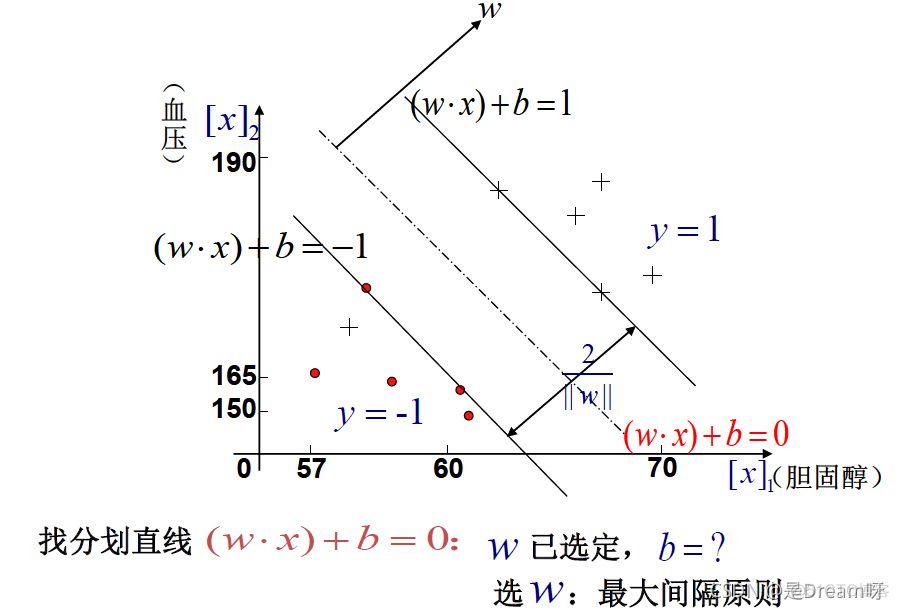
- 2、线性可分问题的最大间隔原则
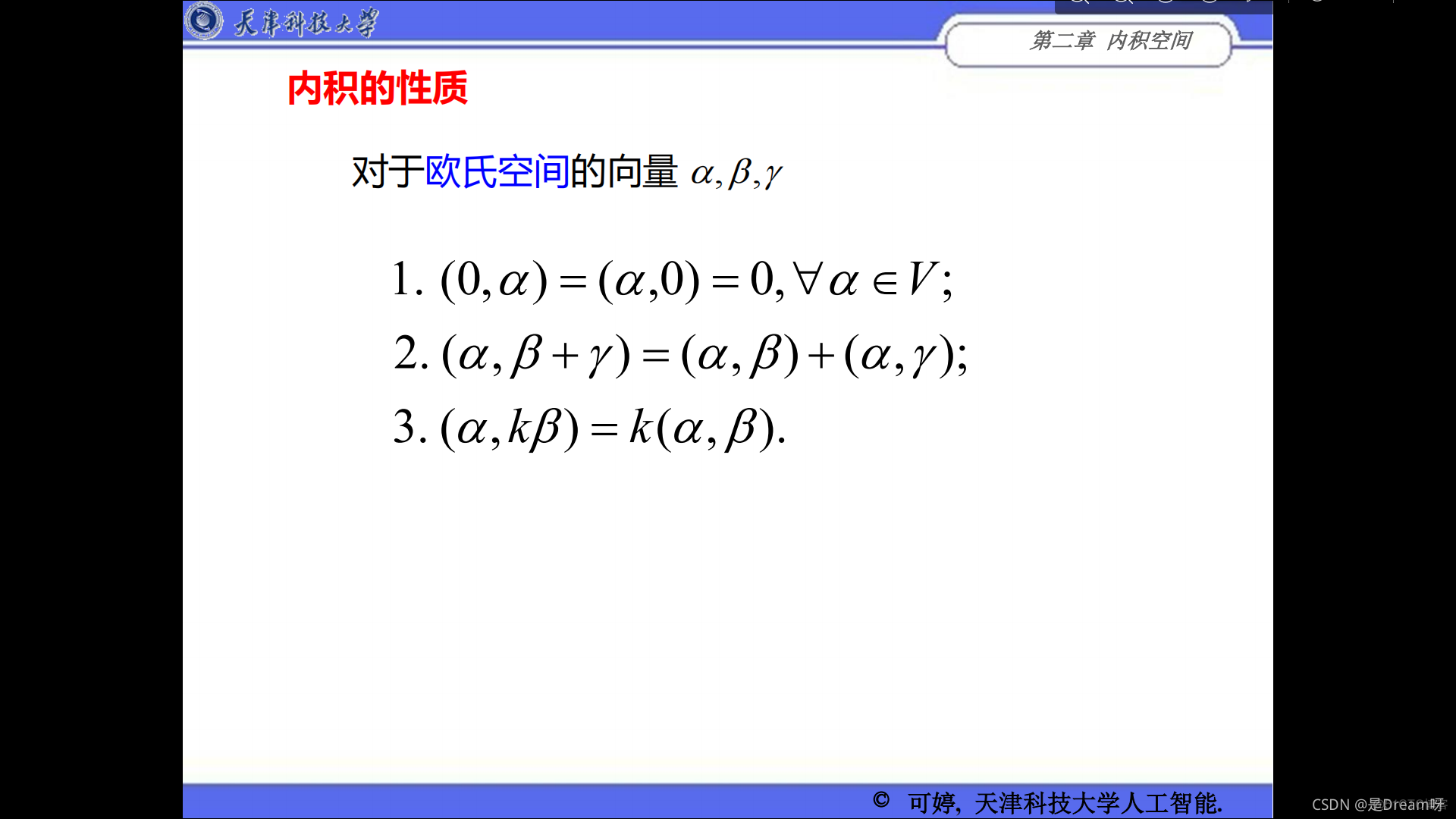
在线性空间中,向量之间仅有加法与数乘两种
代数运算,而无向量长度、向量夹角等度量概念。向量内积正是适应这种要求而引入的。称实内积空间为欧氏空间,称复内积空间为酉空间。
线性空间+ 内积 内积空间
一、内积空间


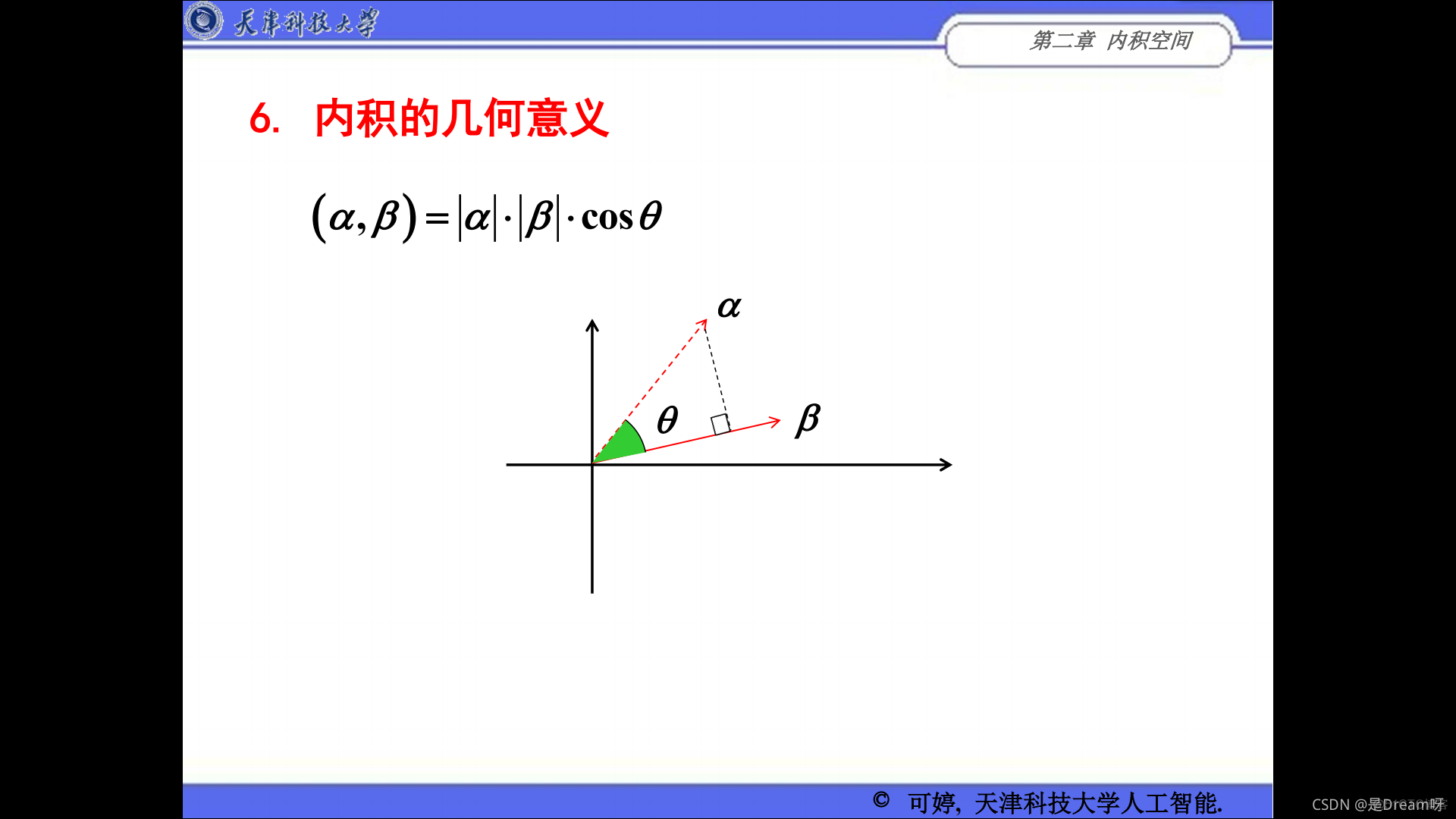
二、 向量的度量



【例一】求向量的夹角:
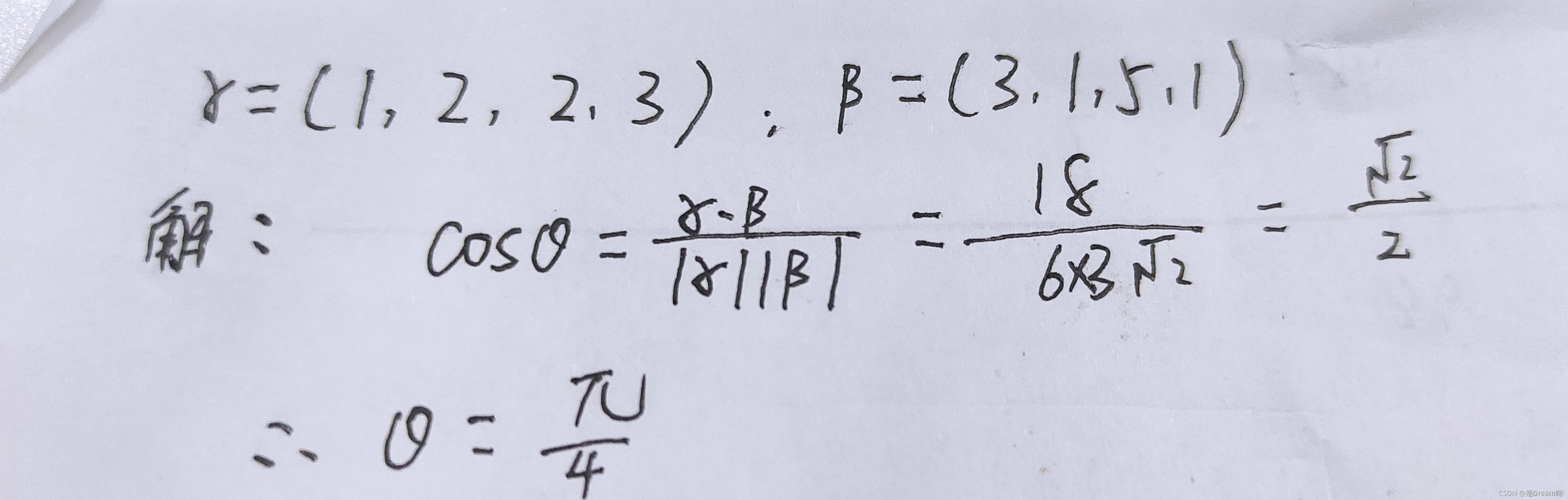
三、向量的正交化方法
1. 正交的概念
当(a,b)=0时,称a和b正交,零向量和任何向量都正交。
2. 正交向量组的概念
若一非零向量组中的向量两两正交,则称该向量组为正交向量组.
说明:
(1)零向量与任意向量都正交;
(2)酉(欧氏空间)中的勾股定理:
3.标准正交向量组(标准正交组)
正交单位向量组成的向量组
4. 正交向量组a1 , , ,an 线性无关
5. 正交基
若 a1 , , ,an是内积空间V 的一个基,且是正交向量组,则称 a1 , , ,an是内积空间V 的一个正交基。
【例2】:
用正交基表示向量,R3的一个正交基。
【例3】:
在R4中求与a1,a2,a3都正交的单位向量。

6. 标准正交基(规范正交基)
7. 若e1,… en 是内积空间V 的一个基,且e1,… en是标准正交向量组,则称e1,… en 是内积空间V的一个标准正交基
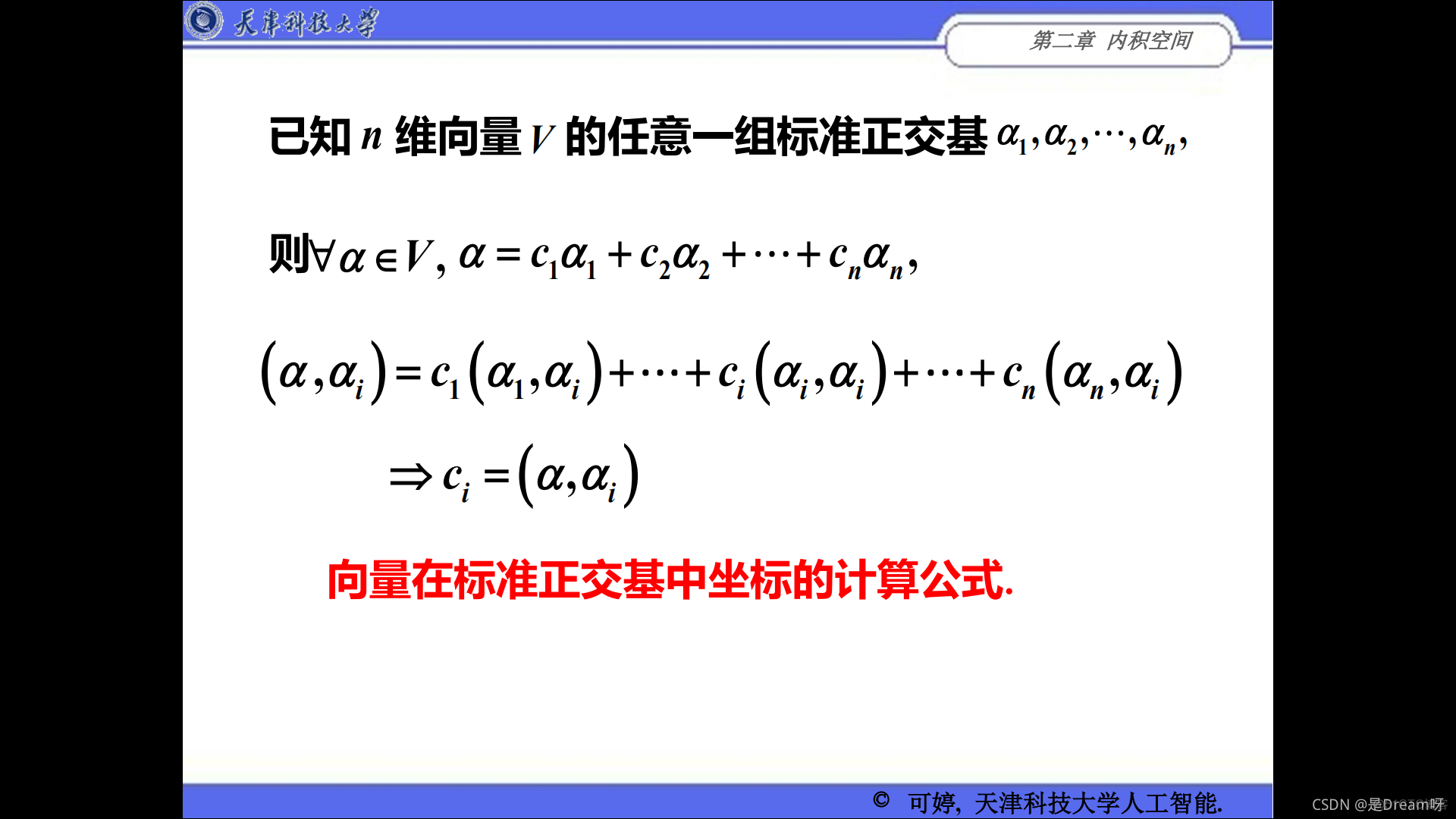
7. 求标准正交向量组的方法(施密特正交化方法)



【例3】用施密特正交化方法,将向量组正交规范化:
a1 (1,1,1,1), a2 (1, -1,0,4), a3(3,5,1, -1)

8、正交矩阵

定理:A为正交矩阵的充要条件是 A 的列(行)向量组都是标准正交向量组.
四、度量矩阵及性质
设 a1,a2 ,a3,an为n维欧氏空间V的基,任何向量可由基表示,表示系数称为该向量的坐标。现任意两个向量的内积有基表示会使什么样?


五、酉空间

6.1 支持向量分类机
1、引例:心脏病诊断
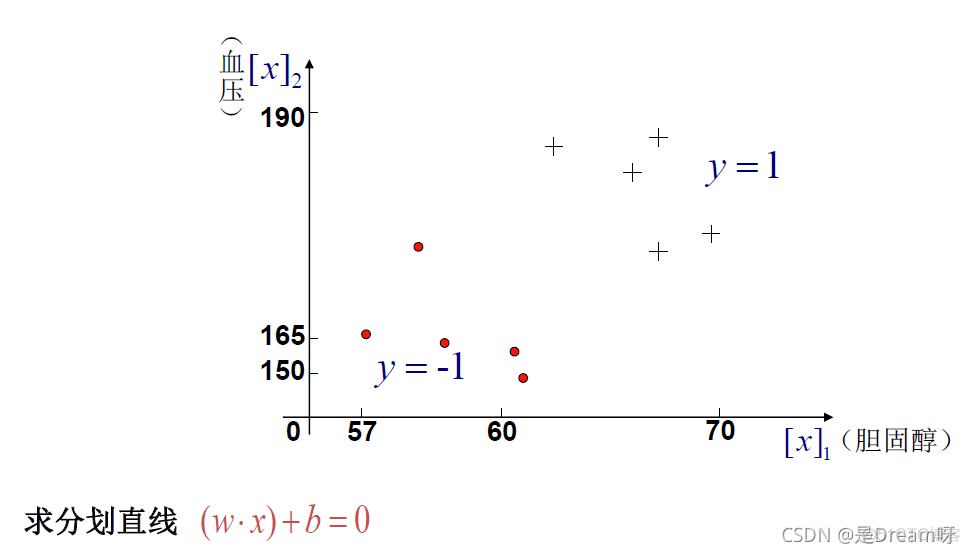
2、线性可分问题的最大间隔原则

好啦,这就是今天要分享给大家的全部内容了
❤️❤️❤️如果你喜欢的话,就不要吝惜你的一键三连了~


