引言

在算法中经常遇到与整数因子有关的问题,常常可以通过质因数分解来巧妙地解决问题:
例如:
60 = 2^2 * 3^1 * 5^1 则60的因子数有(2+1) * (1+1) * (1+1) = 12个
100 = 2^2 * 5^2 则60的因子数有(2+1) * (2+1) = 9个
下面的两个问题可以更深入地理解定理的用法.
问题一 阶乘约数
【问题描述】
定义阶乘n! = 1 * 2 * 3 * 4… * n.
请问100!(100的阶乘)有多少个正约数.
【题解】
100! = 1 * 2 * 3 * 4… * 100,依次分解每个乘数。
定义一个初始化均为0长度为101的数组,储存每个乘数分解后得到的质因数的指数,质因数相同的可以直接指数相加(同底数幂的乘法)。
利用唯一分解定理处理最后得到的数组中的元素,最终得到约数个数。
最终答案为:39001250856960000
【实验结果与讨论】
代码清单 1
a=[0]*101def f(n):
for i in range(2, n+1):
if n==1:
break
while n%i==0:
n/=i
a[i]+=1
for n in range(1, 101 ):
f(n)
s=[int(i)+1 for i in a if i>0]
sum=1
for i in s:
sum*=i
print(sum)
问题二 货物摆放
【问题描述】
小蓝有一个超大的仓库,可以摆放很多货物。现在,小蓝有n箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆L、W、H的货物,满足n = L×W×H。
给定n,请问有多少种堆放货物的方案满足要求。
例如,当n = 4时,有以下6种方案:1×1×4、1×2×2、1×4×1、2x1×2、2×2×1、4x1x1。
请问,当n = 2021041820210418(注意有16位数字)时,总共有多少种方案?
【题解】
先利用唯一分解定理对2021041820210418进行分解。分解结果为2021041820210418 = 2 * 3^3 * 17 * 131 * 2857 * 5882353.然后将得到的质因数进行组合。
由于L * W * H = 2021041820210418,所以只要将它的质因数全部分配给L,W,H即可,分配的方案数即是答案。
对于2,17,131,2857,5882353五个数来说,放入W,L,H的方法数均为3,所以是3^5 = 243种。
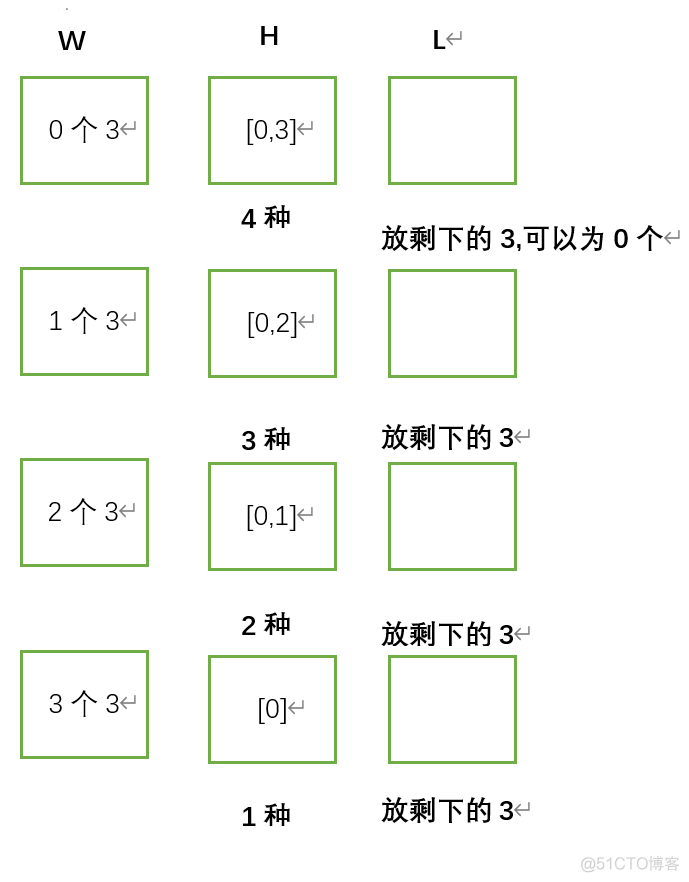
而3个3分别讨论放入W,L,H中不同个数的情况:
① W中3的个数为0,那么L中3的个数可以有0,1,2,3,四种方案,H中就放剩下的3;
② W中3的个数为1,那么L中3的个数可以有0,1,2,三种方案,H中就放剩下的3;
③ W中3的个数为2,那么L中可以有0,1,两种方案,H中就放剩下的3;
④ W中3的个数为3,那么L中可以有0,一种方案,H中放剩下的3。
因此对3个3的分配就有4 + 3 + 2 + 1 = 10种方案。
故答案为 243 * 10 = 2430
容易发现:当某个整数有n个时,将这些整数分配给L,W,H的方案数为:
(n+1) + (n) + (n-1) + (n-2) + ... + 2 + 1 = (n + 2)*(n + 1)/2
据此可以根据分解后质因数的指数计算出方案数,就可写出能够直接得到答案的完整程序代码。
【实验结果与讨论】
对2021041820210418进行质因数分解的程序代码
n=2021041820210418print(n,'= 1',end='')
for i in range(2,n+1):
if n==1:
break
tmp=0
while n%i==0:
tmp+=1
n/=i
if tmp:
print(' * %d^%d'%(i,tmp),end='')
print()
可以直接得出答案的完整程序代码
n=2021041820210418ans=1
for i in range(2, n+1):
if n==1:
break
tmp=0
while n%i==0:
tmp+=1
n/=i
ans*=(tmp+2)*(tmp+1)//2
print(ans)
结语
问题一阶乘约数根据阶乘的运算特点,利用唯一分解定理,直接分解质因数,将得到的质因数的指数存储起来,利用公式最终求解因子数;问题二货物摆放数据范围太大,如果纯暴力枚举寻找它的因子数花费时间太长,利用此定理分解合数,将得到的质因数组合,最终得到答案.以后遇到有关整数因子问题,我们可以首先分析是否能够用唯一分解定理对问题进行求解。
作者:陈相君
