1 简介 为了改善图像融合效率,针对当前图像融合方法存在的局限性,提出一种基于小波变换的多聚焦图像融合方法.首先确定最优的小波分解层数,采用小波变换对图像进行多次分解;然后
1 简介
为了改善图像融合效率,针对当前图像融合方法存在的局限性,提出一种基于小波变换的多聚焦图像融合方法.首先确定最优的小波分解层数,采用小波变换对图像进行多次分解;然后考虑低频子带与高频子带各自的特点,选择局部平均梯度准则作为高频子带的融合规则,低频子带采用3个系数的平均值作为融合规则;最后通过仿真实验对图像融合的有效性进行测试.实验结果表明,该方法获得了更理想的图像融合结果,提高了融合后的图像质量,且融合效果明显优于对比图像融合方法.
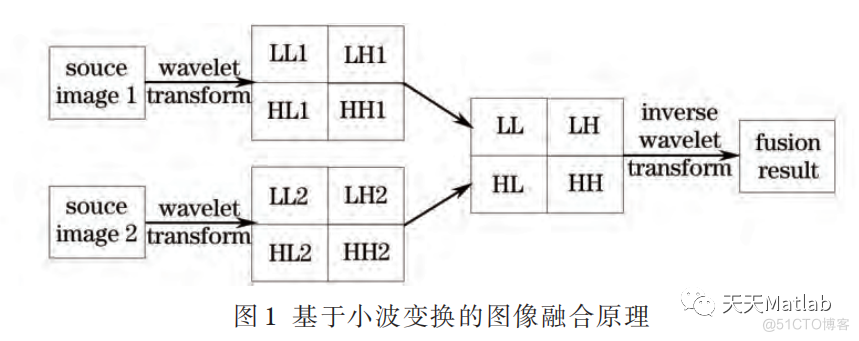
对二维图像进行 J 层的小波分解,可得 3J+1 个不同的频带,其中包含 3J 个高频带和一个低频带。并且能量主要集中于低频部分,而高频部分代表了图像的细节信息。下面以两幅图像的融合为例,说明基于小波变换的图像融合原理。如图 1 所示,对源图像 1 和源图像 2 进行小波分解,即用低通滤波器 L 和高通滤波器 H 分别对两源图像的水平方向和垂直方向进行滤波,使源图像分解为水平低频垂直低频(LL)、水平低频垂直高频(LH)、水平高频垂直低频(HL)、水平高频垂直高频(HH)的 4 个子图像,再根据需要利用低通滤波器 L 和高通滤波器 H 对LL 子图像重复上面的过程,这样就建立各图像的小波塔形分解。接着对分解后的低频子图像和高频子图像根据需要进行融合处理,得到融合后的小波金字塔。最后对融合后的小波金字塔进行小波逆变换,即可得到融合结果。
2 部分代码
function [smat,mp,np] = submat(x,p,level)% 函数 submat 取输入矩阵中以点P为中心、阶数为(2*level+1)的方阵作为输出的子矩阵
[row,col]=size(x);
m=p(1);%行
n=p(2);%列
if (m>row)||(n>col)
error('Point p isout of matrix X !');
return;
end
if((2*level+1)>row)||((2*level+1)>col)
error('Too largesample area level !');
return;
end
% 设置子矩阵的边界值
up=m-level; down=m+level;
left=n-level; right=n+level;
% 若子矩阵的某一边界值超出输入矩阵的相应边界,就进行边界处理,
% 即超出边界后往相反方向平移,使其恰好与边界重合
if left<1
right=right+1-left;
left=1;
end
if right>col
left=left+col-right;
right=col;
end
if up<1
down=down+1-up;
up=1;
end
if down>row
up=up+row-down;
down=row;
end
% 获取作为输出的子矩阵,并计算点p在输出的子矩阵中的位置
smat = x(up:down,left:right);%以点p位中心的 (2*level+1)阶方阵
mp=m-up+1;np=n-left+1; %p点的位置
3 仿真结果


4 参考文献
[1]柏春岚, 刘豪. 基于小波变换的图像融合及其MATLAB实现[J]. 科技广场, 2014.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

