KMeans聚类算法
- 何为聚类?
- 聚类与分类的区别
- 常见聚类算法及KMeans算法
- 算法实现步骤
- KMeans的优缺点
- KMeans聚类算法实例
- 完整代码
何为聚类?
俗话说“物以类聚,人以群分”说的是把相同或相似的东西放在一起比较讨论,志同道合的朋友常常能够相聚在一起把酒言欢。朋友间正是因为有相同的志向和趣味,所以能够走到一起,与人一样,数据挖掘里面的聚类是指把具有相同或者相似(退后一步)的对象放在一起讨论,从而挖掘出放在一起的理由和不放在一起的理由以及这样放在一起与不放在一起所带来的额外效用。也许你会问用什么办法来衡量两个对象的相似性呢?这时候就需要把对象的各种属性考虑进来,通过对比分析两个对象的不同属性间的差异来进行判断,比如考察某个班所有学生的聚类情况,已经知道所有学生的期末考试成绩以及平时缺课次数两个属性,可以按照下面规则聚集
学神
期末考试成绩优异,平时缺课无数学霸
期末考试成绩优异,平时不缺课学渣
期末考试成绩掉渣,平时缺课无数学弱
期末考试成绩掉渣,平时不缺课
我们看到了按照成绩属性取优异还是掉渣以及缺课属性取缺还是不缺共4种组合可以把班里所有学生划分成4类,这样每一类的学生都有自己的特点,同类别的学生有着非常高的相似度,不同类的学生却是天壤之别。这里,我们又引进了相似度的概念,如果两个对象各属性相似度高,那么这两个对象理应属于同一类别,反之应该属于不同类别,上面我们只是通过描述性的语言来说明分类情况, 那么如何用数学语言来刻画呢? 常见的相似度刻画采用距离公式,主要有以下几种距离公式,为讨论的一般性,我们假设有 n n n个样本,每个样本有 p p p个指标,数据矩阵如下表所示
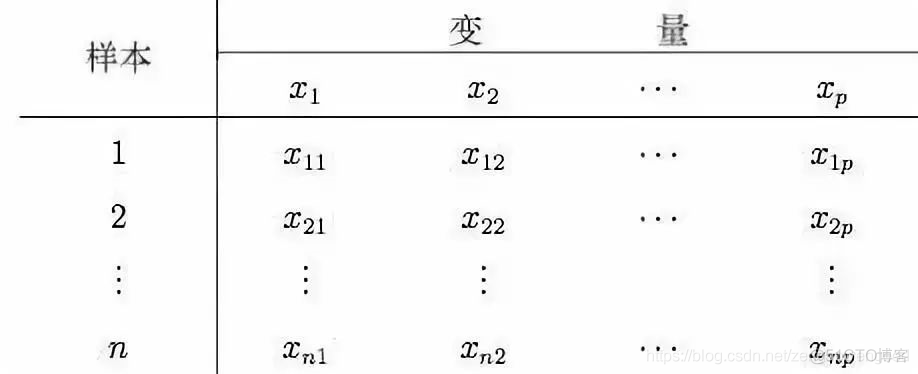
记第 i i i个样本为 ( i ) = ( x i 1 , ⋯ , x i p ) T (i)=(x_{i1},\cdots,x_{ip})^T (i)=(xi1,⋯,xip)T,第 j j j个样本为 ( j ) = ( x j 1 , ⋯ , x j p ) T (j)=(x_{j1},\cdots,x_{jp})^T (j)=(xj1,⋯,xjp)T,把每个样本看成 p p p维空间里的质点,记 ( i ) (i) (i)与 ( j ) (j) (j)的距离为 D ( i , j ) D(i,j) D(i,j) , 那么
欧式距离(Euclidean Distance)
D ( i , j ) = [ ∑ l = 1 p ∣ x i l − x j l ∣ 2 ] 1 2 D(i,j)=[ \sum\limits_{l=1}^{p}|x_{il}-x_{jl}|^2 ]^ {\frac{1} {2} } D(i,j)=[l=1∑p∣xil−xjl∣2]21曼哈顿距离(Manhattan Distance)
D ( i , j ) = ∑ l = 1 p ∣ x i l − x j l ∣ D(i,j)=\sum\limits_{l=1}^{p}|x_{il}-x_{jl}| D(i,j)=l=1∑p∣xil−xjl∣切比雪夫距离 (Chebyshev Distance )
D ( i , j ) = m a x 1 ≤ l ≤ p ∣ x i l − x j l ∣ D(i,j)=max_ {1\leq l\leq p} |x_{il}-x_{jl}| D(i,j)=max1≤l≤p∣xil−xjl∣闵可夫斯基距离(Minkowski Distance)
D ( i , j ) = [ ∑ l = 1 p ∣ x i l − x j l ∣ q ] 1 q D(i,j)=[ \sum\limits_{l=1}^{p}|x_{il}-x_{jl}|^q ]^ {\frac{1} {q} } D(i,j)=[l=1∑p∣xil−xjl∣q]q1
从各种距离公式可以看出,切比雪夫距离和欧式距离是闵科夫斯基距离当 q = 1 q=1 q=1和 q = 2 q=2 q=2的特殊情况。
聚类与分类的区别
很多初学者会把聚类和分类混肴,那么聚类和分类有何区别呢?主要体现在
学习范畴
分类属于监督学习范畴,而聚类属于无监督学习范畴进程不一样
分类主要用训练数据学习一个模型,里面数据的类别是确定的,然后把测试集中的实例对应到这些确定的类别中,是两步走的过程。而聚类是起初并不知道具体有多少类,可以先行假定类别数,即 k k k 值,然后通过某些判断方法,把所有数据划分到这 k k k个类别中,使得同一类的实例尽可能聚集到一起,不同类实例尽量离间,不需要训练测试,更多像一锤子买卖。
常见聚类算法及KMeans算法
常见的聚类算法有基于空间测距的KMeans算法,基于密度划分的DBSCAN算法,基于点距离的 hierarchical clustering算法,基于图距离的Affinity Propagation算法等,这里重点介绍KMeans算法。
KMeans翻译成中文表示k均值,KMeans算法的关键是找 k k k个均值来当作类别的中心,并以此为参考将其他实例吸收到这 k k k个类别,使得最后距离和最小。假设有 n n n个实例,现在要将其划分到 k k k个不相邻的类别或簇 C = { c 1 , ⋯ , c k } \mathcal{C}=\{c_1,\cdots,c_k\} C={c1,⋯,ck},记第 j j j个簇 c j c_j cj中的样本均值(中心)为 u j u_j uj, KMeans 算法旨在选择合适的 u j u_j uj,使得簇内平方和最小,即
min u j ∈ C ∑ j = 1 k ∑ i = 1 n ∣ ∣ x i − u j ∣ ∣ 2 \min\limits_ {u_j\in C}\sum\limits_{j=1}^k\sum\limits_{i=1}^n||x_i-u_j||^2 uj∈Cminj=1∑ki=1∑n∣∣xi−uj∣∣2
算法实现步骤
KMeans算法比较简单,只有三步
如果前后两次计算得到簇中心不发生变化,或者变化小于给定的阈值,算法结束,否则返回2计算每个样本到新的簇中心的距离
KMeans的优缺点
KMeans算法假设簇都是凸的且同性的,而对长条形和不正规的形状表现不好,对于高维数据,KMeans算法会消耗更多计算资源。
KMeans聚类算法实例
完整代码
# -*- coding: utf-8 -*-"""
project_name:聚类算法
@author: 帅帅de三叔
Created on Wed Nov 6 10:05:42 2019
"""
import pandas as pd #导入数据分析模块
from sklearn import preprocessing #导入数据预处理模块
from sklearn.cluster import KMeans #导入kmeans聚类算法
data=pd.read_excel("2018vs2016.xlsx",index_col=u"板块名称",sheet_name="2018") #读取数据
X=data.iloc[:,0:-1] #聚类用到的特征属性
X_scaled=preprocessing.StandardScaler(copy=True,with_mean=True,with_std=True).fit_transform(X) #特征属性标准化
feature=pd.DataFrame(X_scaled)
k=4 #设置聚类类别数
maxiteration=500 #设置最大迭代次数
model=KMeans(n_clusters=k,init='k-means++',n_init=10,max_iter=maxiteration,tol=1e-4,precompute_distances='auto',verbose=0,random_state=None,copy_x=True,n_jobs=2,algorithm='auto') #聚类模型初始化
model.fit(feature,y=None,sample_weight=None) #训练模型
lables=pd.DataFrame(model.labels_,index=data.index) #类别标签
cluster_result=pd.concat([data,lables],axis=1) #沿着水平方向拼接类别标签
cluster_result.columns=["交通","商业购物","教育","医疗","景观周游","生活娱乐","综合得分","类别标签"] #重命名表头
print(cluster_result)
cluster_result.to_excel("板块聚类结果.xlsx")

