1 简介 TSP问题是典型的NP-hard组合优化问题,采用模拟退火+蚁群+遗传算法分别求解。 2 部分代码 function Shortest_Length=SATSP(C) a=0.99;%温度衰减函数的参数 t0=99; tf=3; t=t0; MarkobLength=10000;%Markob链
1 简介
TSP问题是典型的NP-hard组合优化问题,采用模拟退火+蚁群+遗传算法分别求解。
2 部分代码
function Shortest_Length=SATSP(C)a=0.99;%温度衰减函数的参数
t0=99;
tf=3;
t=t0;
MarkobLength=10000;%Markob链长度
n=size(C,1);%城市的数目
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;%简单地求两点之间的距离
else
D(i,j)=eps;%应该赋值为0,但因为后面启发因子需要取倒数,所以用eps表示,eps为当发现某个值小于eps时,就把这个数当做0来处理
end
D(j,i)=D(i,j);%对称矩阵
end
end
R_new=1:n;%产生初始解
%sol_new是每次产生的新解;sol_current是当前解;sol_best是冷却中的最好解
L_current=inf;%当前距离
Shortest_Length=inf;%当前最好距离
%初始化
R_current=R_new;
R_best=R_new;
p=1;
while t>=tf
t
for r=1:MarkobLength
%产生扰动
if(rand<0.5)%随机决定是两交换还是三交换
%两交换
i1=0;i2=0;
while(i1==i2)
i1=ceil(rand.*n);
i2=ceil(rand.*n);
end
tmp1=R_new(i1);
R_new(i1)=R_new(i2);
R_new(i2)=tmp1;
else
% 三交换
i1 = 0; i2 = 0; i3 = 0;
while (i1 == i2) || (i1 == i3)|| (i2 == i3) || (abs(i1-i2) == 1)
i1 = ceil(rand.*n);
i2 = ceil(rand.*n);
i3 = ceil(rand.*n);
end
tmp1 = i1;tmp2 = i2;tmp3 = i3;
% 确保i1 < i2 < i3
if (i1 < i2) && (i2 < i3)
elseif (i1 < i3) && (i3 < i2)
i2 = tmp3;i3 = tmp2;
elseif (i2 < i1) && (i1 < i3)
i1 = tmp2;i2 = tmp1;
elseif (i2 < i3) && (i3 < i1)
i1 = tmp2;i2 = tmp3; i3 = tmp1;
elseif (i3 < i1) && (i1 < i2)
i1 = tmp3;i2 = tmp1; i3 = tmp2;
elseif (i3 < i2) && (i2 < i1)
i1 = tmp3;i2 = tmp2; i3 = tmp1;
end
tmplist1 = R_new((i1+1):(i2-1));
R_new((i1+1):(i1+i3-i2+1)) =R_new((i2):(i3));
R_new((i1+i3-i2+2):i3) = tmplist1;
end
%检查是否满足约束
%计算目标函数
L_new=0;
for i=1:(n-1)
L_new=L_new+D(R_new(i),R_new(i+1));
end
%再计算从最后一个城市到第一个城市的距离
L_new=L_new+D(R_new(n),R_new(1));
if L_new<L_current
L_current=L_new;
R_current=R_new;
if L_new<Shortest_Length%把冷却结果中最好的解保存下来
Shortest_Length=L_new;
R_best=R_new;
end
else
%若新解的目标函数值小于当前解的,则仅一定概率接受新解
if rand<exp(-(L_new-L_current)./t)
L_current=L_new;
R_current=R_new;
else
R_new=R_current;
end
end
end
t=t.*a;%控制参数t(温度)减少为原来的a倍
drawRoute(C,R_best,t,Shortest_Length);
end
drawRoute(C,R_best,t,Shortest_Length);
disp('最优解为:')
disp(R_best)
disp('最短距离:')
disp(Shortest_Length)
end
function drawRoute(C,R_best,t,minLu)
for i=1:length(C)
plot(C(i,1),C(i,2),'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');
hold on;
end
x=C([R_best R_best(1)],1);
y=C([R_best R_best(1)],2);
plot(x,y,'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');
text(3,30,['第 ',num2str(t),' 度',' 最短距离为 ',num2str(minLu)]);
title('模拟退火算法优化路径')
hold off
pause(0.05);
end
3 仿真结果
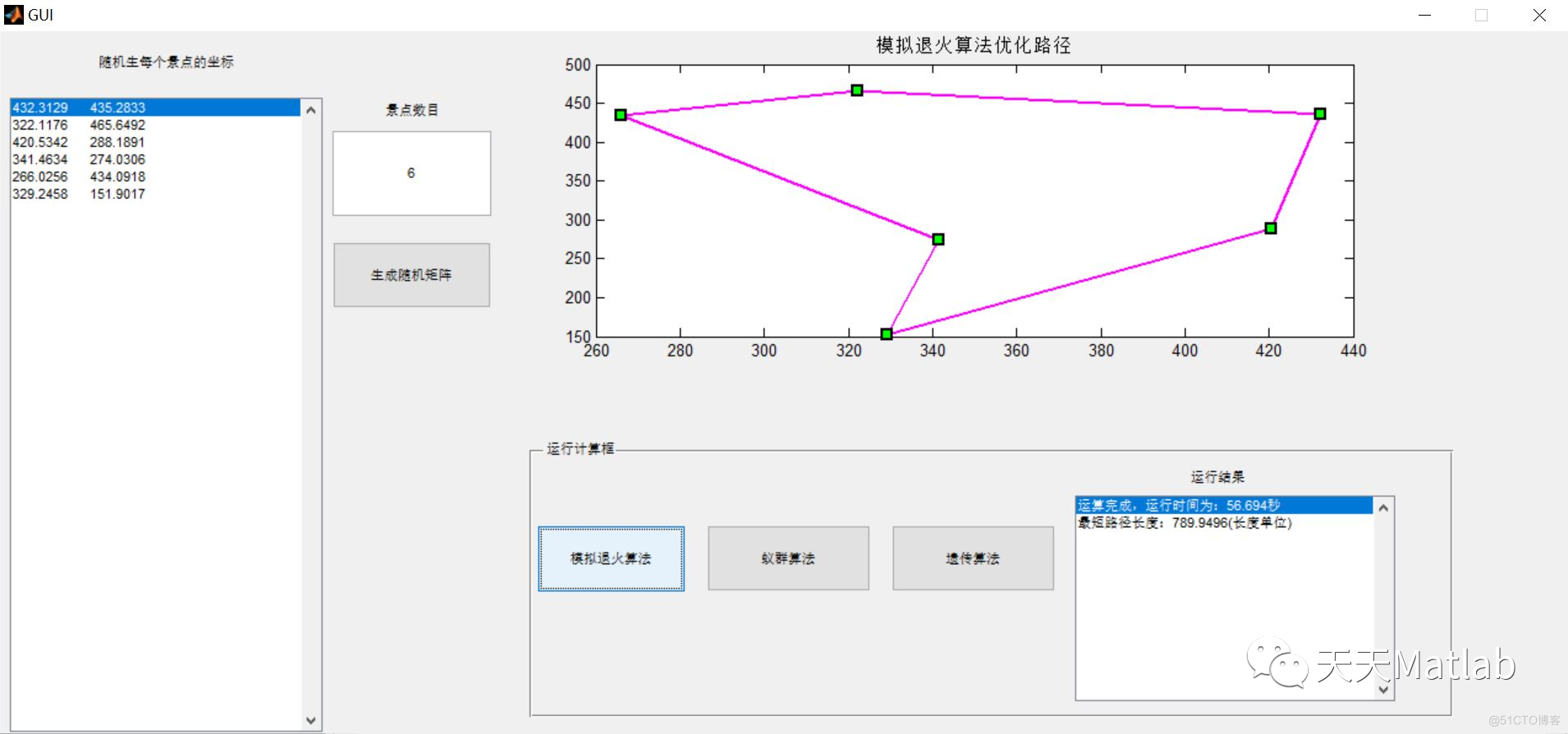
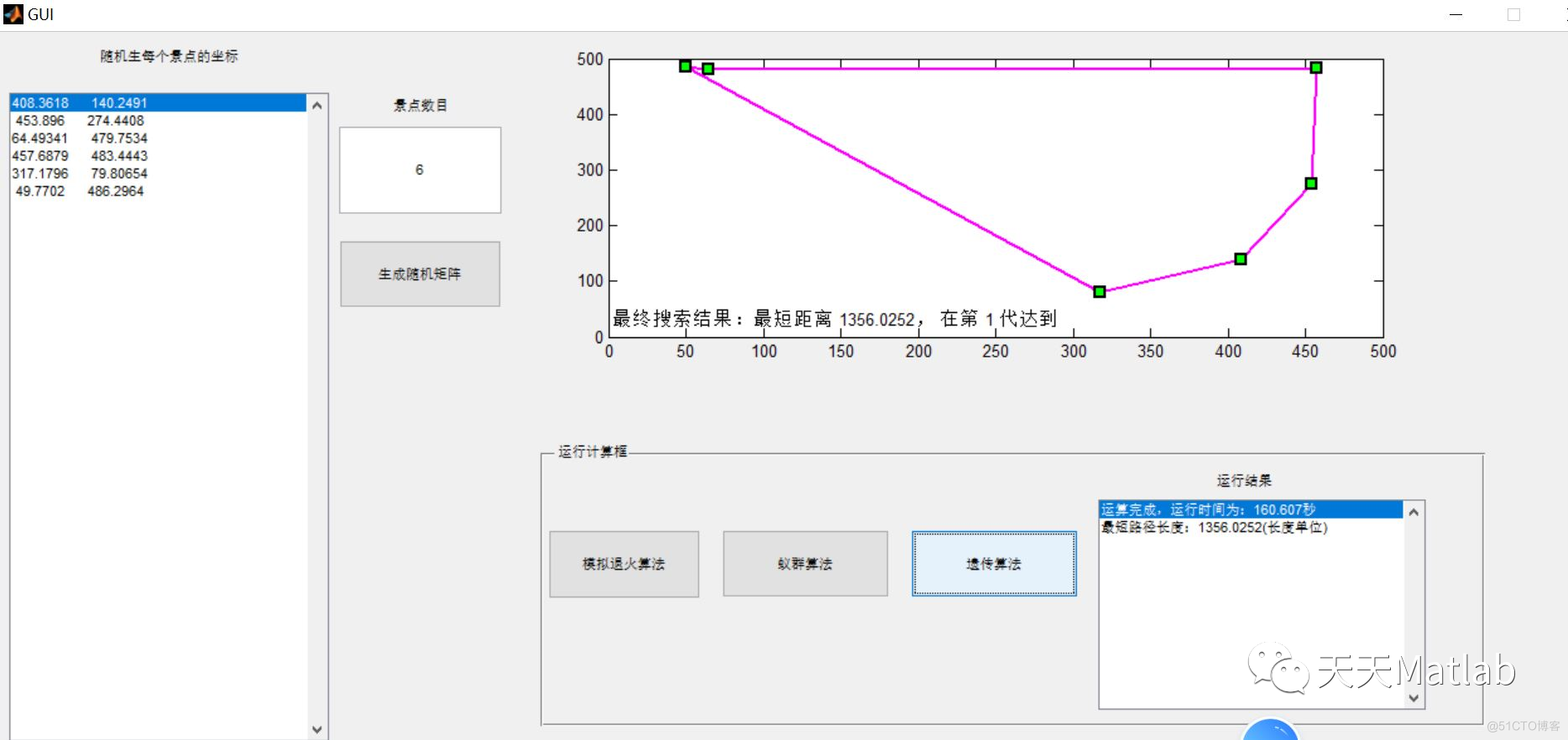
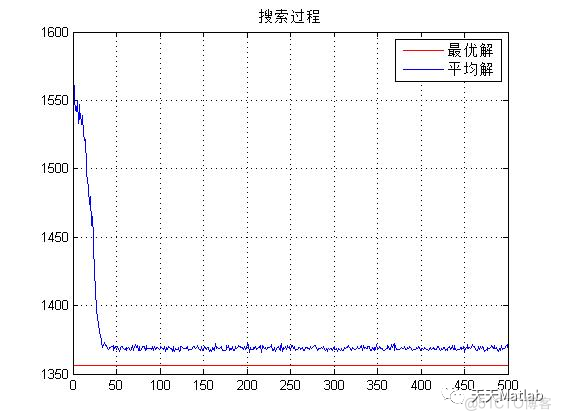
4 参考文献
[1]杜宗宗, 刘国栋. 基于混合遗传模拟退火算法求解TSP问题[J]. 计算机工程与应用, 2010, 46(29):4.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

