1 简介
基于LSB+DWT+DCT三种算法实现图像和音频水印嵌入提取。
1.1 LSB算法
根据LSB算法简单易实现的特点,结合在图像置乱技术中很好特性的Arnold变换。利用变化产生影子图像。通过LSB算法将影子图像嵌入到掩饰图像中,再利用LSB算法将图像的影子图像提取出来。将提取出来的影子图像经过文中设计的Arnold反变换恢复出原始。该方法不但有效地无损伤隐藏了图像,同样还保证了隐藏图像的安全性,无损伤性。
1.2 小波变换算法
**2 基于DWT的音频水印算法**
**2.1 水印嵌入**
本文研究的音频水印算法是基于离散小波变换 (DWT) , 音频信号通过DWT变换, 在变换域中嵌入水印信息, 再经过逆变换 (IDWT) 从而得到嵌入水印的音频信号。水印嵌入原理框图如图1所示。
假定水印为M1×M2的二维图像bw, 由于音频信号通常为一维向量, 故水印信息在嵌入音频信号之前需要将二维降至一维向量w, 即M=M1×M2。通常我们也可以将图像进行打乱加密, 增强水印隐蔽性。
假定语音信号为s, 长度为N, 则s={s1, s2, s3, …, sN}由于语音信号较长在处理中一般需要进行分段, 每段长度设为N1, 故该语音信号分为K=fix (N/N1) 段进行处理, 每段语音均嵌入一个水印信息。
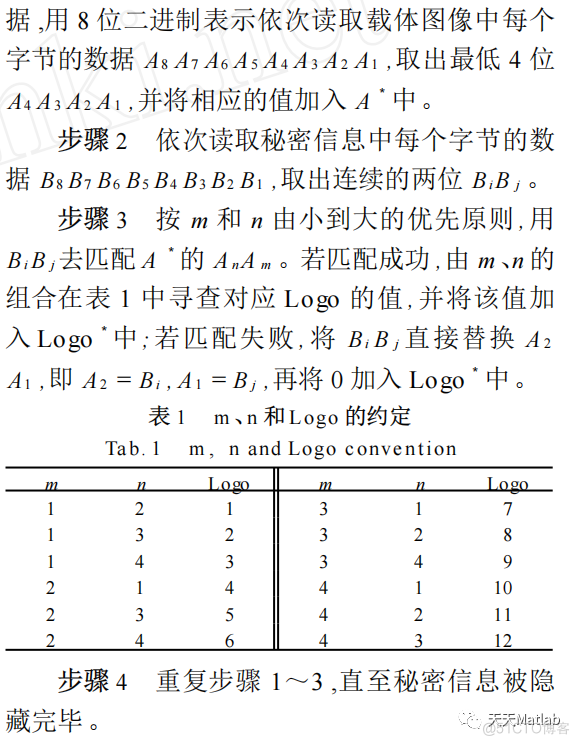
小波变换是为了解决傅立叶变换的不足而提出的一种分析变换, 傅立叶变换的基函数是铺满整个时域的正弦信号, 对于突变信号以及变化的频率成分信息均不能较准确地表示。而小波变换是时间和频率的局部变换, 更能准确地表示音频信号的频域特征, 常用的小波基有Haar小波、Daubechies (db N) 小波、Marr小波等。本文采用的小波基是Haar小波, 它是支撑域在t∈[0, 1]范围内的矩形波, 定义如下:
图1 音频信号水印嵌入原理框图
图2 音频信号水印提取原理框图
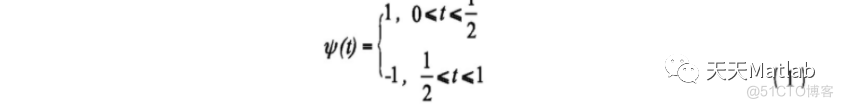
取定Haar小波基后, 则语音信号s可以表示为:
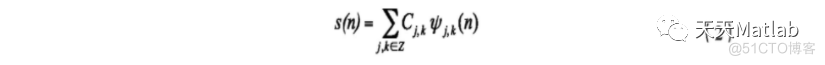
其中Cj, k为离散小波系数, 将音频信号分解为低频的近似部分和高频的细节部分, 我们在水印信息的嵌入处理中, 主要针对代表低频近似部分的系数向量处理, 即将水印信号放入低频近似部分, 高频细节部分不变, 以保证语音质量基本不变。由于嵌入的水印为二值图像, 因此如果水印信息的值为1, 则将对应的低频系数增大, 相反如果值为0, 则将对应的低频系数降低。在DWT域嵌入水印信息后, 然后通过IDWT变换, 将语音信号变换成时域信号。
**2.2 水印提取**
为了保证信息安全, 在发送端发送嵌入水印的音频信号, 而在接收端为了确定音频信息的准确性, 我们通常需要提取水印以确保来源的真实性, 因此水印的提取技术也尤为重要。在水印提取过程中, 需要原始音频信号与嵌入水印的音频信号同时进行DWT, 再将两者参数进行分析比较提取出水印信息。水印提取原理框图如图2所示。
在前面所述的水印嵌入过程中, 将水印信息嵌入高频的细节部分, 因此在提取水印过程中, 我们也只需比较原始语音信号S的低频小波系数向量c A与嵌入水印的音频信号s1的低频小波系数向量c A1作比较, 若c A1>c A, 则水印信息为1;反之则为0, 再通过向量平均, 如此得到水印信息的一维向量, 最后通过升维得到二值图像.
1.3 DCT算法
在图像隐写分析中，这几个特征是比较经典的 图像隐写分析中DCT特征与Markov特征展现出了极大a的潜力，小波变换的奇异值分解（Wavelet Singular Value Decomposition ， WSVD）特征也有奇效，本文实现前人论文的特征提取编程代码。 先说说理论知识 1 扩展DCT统计特征提取 大多数的隐密算法都是对JPEG图像的DCT系数进行操作，以此来嵌入秘密信息。DCT系数统计特征，旨在捕捉DCT系数的统计量的特征，以此来区分载体图像和隐密图像。 DCT系数统计算法由Fridrich【1】提出，其中包含了DCT系数直方图，共生矩阵，空域块间相关性等部分。首先用DCT系数替换相同位置的原始图像像素，使用dij(k) 来表示DCT系数矩阵，其中i，j=1, … ,8，k=1, … ,nB。而dij(k)则代表的是在第k个8×8 DCT块中处于(i，j)位置的DCT系数，而DCT块一共有nB 块。为了减少计算量和特征维度，在计算特征之前需要进行预处理，将所有DCT系数值范围限定在[-5，5]之间，大于和小于该范围内的值全部变换为-5到+5之间。 
其中，Ir和Ic表示图像DCT系数块的两种排列方式，分别是行扫描顺序和列扫描顺序。 接下来的两个特征Bα是从解压的JPEG图像中计算，也是一种块间相关性的特征： 
在DCT系数统计的隐密分析中，Fridrich首次提出了用于隐密分析的“校准”概念和计算原理：特征计算函数F，训练或测试图像J1，将图像J1解压到空域并沿各个方向裁剪四个像素，然后使用同J1相同的量化表压缩得到的图像J2。f表示最终获取的特征，而最后的特征由f=F(J1)-F(J2)计算得到。
采用如此计算方式的原理如下：裁剪之后的图像和原始图像内容上大体上完全一致，虽然裁剪之后的图像失去了原来的DCT分块，但是其统计特征应与原来相差不多。而这个过程会对嵌入的信息十分敏感，使裁剪前后的特征差别较大。经过实验证明，如此提取特征的方法非常有效果。
总结来说，DCT系数统计特征对DCT系数全局和局部进行了统计分析，并且捕获DCT系数的块间相关性和空域像素的相关性等特征。对于JPEG图像来说，所有隐密算法都是针对DCT系数进行修改，该算法确实是有一定的效果。实验中，该特征集展现了不错的分析效果，在0.2的嵌入率情况下可以达到平均95%的准确率，但是对MB算法的效果一般，尤其是MB2。
原始DCT统计特征已经有一定的检测效果，本文先对其进行扩展，加强特征的检测效果。对于全局直方图函数H，可以得到范围在[-5，+ 5]中的元素个数的差异，包括全局直方图和局部直方图，局部直方图选择的位置为{(1, 2)，(2, 1)，(3, 1)，(2, 2)，(1, 3)}。因此，直方图特征是： 
如此的DCT扩展特征共有193维，其特征组成见下表。 
2 部分代码
function image_b = LSB(original,watermark)%隐藏矩阵存到I中，隐藏信息存到J中
L =original;
J=watermark;
%N为隐藏矩阵大小
N=64;
%K为分块大小1
K=8;
%p,q为变换系数
p=2;
q=1;
%
%隐藏思想：将512*512的矩阵分为64*64个8*8的方块，根据p,q选出方块中某一个元素，根据LSB方法隐藏0或1
%p,q变换：p初始值为2，q初始值为1，每对一个8*8矩阵嵌入完信息，p新值为q+2对8求模的值加1（求模得出的值可能为1），同理q新值为p+2对8求模的值加1
%此方法适用与频域隐藏，不适用于普通LSB隐藏
%隐藏信息嵌入方法：对选出的值进行二进制变换，转为二进制后比较倒数第二位和最后一位的差值（倒数第二位减去最后一位），差值为0表示嵌入0，差值为1表示嵌入1
%
for m=1:N
for n=1:N
x=(m-1)*K+1;
y=(n-1)*K+1;
%取出一个8*8分块
block=L(x:x+K-1,y:y+K-1);
%取出方块所选值的倒数第二位
temp0 = bitget(block(p,q),2);
%取出方块所选值的最后一位
temp1 = bitget(block(p,q),1);
%求出差值
temp = double(temp0) - double(temp1);
%嵌入信息为0时
if(J(m, n)==0)
%差值为1时，所选值最后2位为10，减2后变为00，差值为0
if(temp == 1)
block(p,q) = block(p,q) - 2;
end
%差值为-11时，所选值最后2位为01，减1后变为00，差值为0
if(temp == -1)
block(p,q) = block(p,q) - 1;
end
%嵌入信息为1时
else
%差值为0时，所选值最后2位为00或11
if(temp == 0)
%最后2位为00时，加2后最后两位为10，差值为1
if(mod(block(p,q),2)==0)
block(p,q) = block(p,q) + 2;
%最后2位为11时，减1后最后两位为10，差值为1
else
block(p,q) = block(p,q) - 1;
end
end
%差值为-1时，所选值最后2位为01，加1后最后两位为10，差值为1
if(temp == -1)
block(p,q) = block(p,q) + 1;
end
end
%将嵌入隐藏信息后的矩阵放回原矩阵
L(x:x+K-1,y:y+K-1)=block;
%对p,q进行变换
p=p+2;
q=q+2;
p=mod(q,8)+1;
q=mod(p,8)+1;
end
end
image_b = uint8(L);
return
3 仿真结果
4 参考文献
[1]张元钦. 基于DWT-DCT的图像数字水印技术的研究. Diss. 北京邮电大学, 2014.
博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。
部分理论引用网络文献，若有侵权联系博主删除。
