【背包问题】基于粒子群算法求解多目标背包问题含Matlab源码

1 简介

提出一种基于博弈论的多目标粒子群算法.算法中将每个目标函数看成是一个智能体,智能体控制种群往自己最有利的方向进行搜索,然后将它看成是参与博弈的一个参与人.采用存在一个博弈序列的重复博弈模型,在重复博弈中,并不是每次博弈都产生最大效益,而是要总的效益最大化.将算法用于求解多目标0/1背包问题.仿真实验结果表明,该算法能够找到接近Pareto最优前端的更好的解,同时维持解分布的均匀性.

2 部分代码

%% 该函数演示多目标perota优化问题
%清空环境
clc
clear
load data
%% 初始参数
objnum=size(P,1); %类中物品个数
weight=92; %总重量限制
%初始化程序
Dim=5; %粒子维数
xSize=50; %种群个数
MaxIt=200; %迭代次数
c1=0.8; %算法参数
c2=0.8; %算法参数
wmax=1.2; %惯性因子
wmin=0.1; %惯性因子
x=unidrnd(4,xSize,Dim); %粒子初始化
v=zeros(xSize,Dim); %速度初始化
%去掉重复粒子
repflag=0; %重复标志
k=1; %不同非劣解粒子数
flj2=[]; %存储不同非劣解
fljx2=[]; %存储不同非劣解粒子位置
flj2(k,:)=flj(1,:);
fljx2(k,:)=fljx(1,:);
for j=2:size(flj,1)
repflag=0; %重复标志
for i=1:size(flj2,1)
result=(fljx(j,:)==fljx2(i,:));
if length(find(result==1))==Dim
repflag=1;%有重复
end
end
%粒子不同，存储
if repflag==0
k=k+1;
flj2(k,:)=flj(j,:);
fljx2(k,:)=fljx(j,:);
end
end
%非劣解更新
flj=flj2;
fljx=fljx2;
end
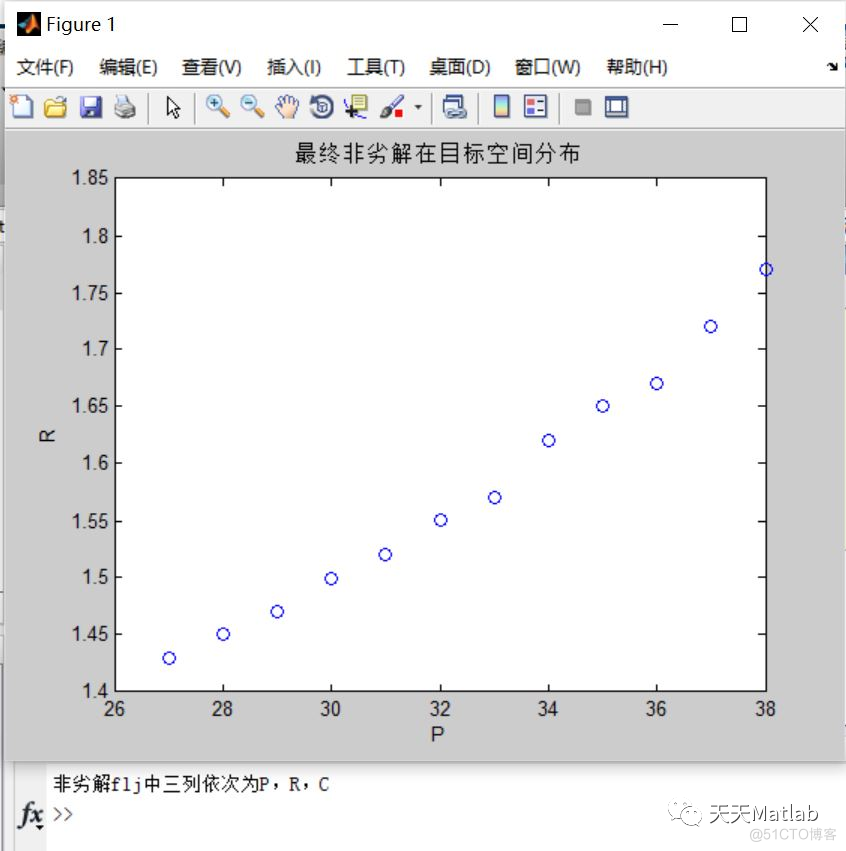
%绘制非劣解分布
plot(flj(:,1),flj(:,2),'o')
xlabel('P')
ylabel('R')
title('最终非劣解在目标空间分布')
disp('非劣解flj中三列依次为P，R，C')

3 仿真结果

4 参考文献

[1]邓子龙, 程芳. 基于粒子群算法的多目标背包问题求解[J].  2022(3).

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。