1 简介
基于互信息的配准方法具有精度高,鲁棒性强的特点,成为近年来图像配准研究的热点.但基于互信息的目标函数存在许多局部极值,为配准的优化过程带来了很大的困难.该文提出了一种蚁群算法和Powell法相结合的多分辨率搜索优化算法.该算法以互信息作为相似性测度,采用基于小波变换的多分辨率策略,将蚁群算法与Powell法结合起来对2维的CT,MR图像进行了配准.实验结果表明,这种方法能够有效地克服互信息函数的局部极值,大大地提高了配准精度,达到亚像素级.
蚁群算法在一般情况下均能找到比较满意的结果,但得到的解不一定是解空间的最优解,通常是全局最优解附近的一个解。而 Powell 算法有极强的局部寻优能力,所以在本文的配准优化过程中我们将蚁群算法的全局搜索能力和Powell 算法的局部寻优能力有机结合起来。由于蚁群算法中目标函数的计算次数比较多,从而优化时间比较长,为此我们采用了基于小波变换的多分辨率策略,优化过程分为两步,第 1 步首先在较低分辨率的图像上采用蚁群算法进行配准,此时图像比较小,互信息计算速度快,优化过程能较快完成;第 2 步采用 Powell 法在高分辨率图像上进行寻优,算法的初始点为上一步中蚁群算法得到的最好解。该算法的具体步骤描述如下:
(1)首先对待配准的浮动图像和参考图像进行小波分解,得到比较小的子图像;对子图像进行配准,采用蚁群算法进行寻优。优化过程中插值方法采用最近邻法,联合灰度直方图的灰度级数设置为 64。在图像分辨率比较低时,采用最近邻法插值速度快,效果和 PV 插值差不多,将图像灰度归一化到较少的灰度级别能够提高配准精度和速度。
(2)将步骤(1)中蚁群算法得到的配准参数作为 Powell 法寻优的起始点,在高分辨率的图像上进行配准,得到配准的最优解。为提高配准精度,优化过程中插值方法采用 PV 插值,图像灰度级数设置为 256。
由于步骤(1)中蚁群算法的配准结果为步骤(2)中的Powell 法优化提供了一个非常有效的初始点,使得 Powell法的参数优化顺序对其优化结果的影响很小,因此不需要根据成像特点来设定参数优化顺序,同时也使得步骤(2)的优化时间要比从默认初始点或者随机初始点开始搜索的普通的Powell 法花费的时间短很多。步骤(1)中的蚁群算法是在分辨率低的图像上进行寻优,并且插值方法简单,所以互信息的计算比较快,步骤(1)的优化过程能在比较短的时间内完成,整个算法总的运行时间与普通的 Powell 法相当
2 部分代码
function [FusionImage,RegistrationImage]=Fusion(handles)%%%%%%%%%%%%%%%%%%%%获取原图像及配准参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
I=handles.Old_I;
J=handles.Old_J;
y=handles.RegistrationParameters(1);
x=handles.RegistrationParameters(2);
ang=-handles.RegistrationParameters(3);
%%%%%%%%%对浮动图像空间变换及插值,以便得到配准后的输出图像%%%%%%%%%%%%%
[nrows,ncols]=size(J);
width=nrows;
height=ncols;
new_J=uint8(zeros(width,height));
a=(width-1)/2;
c=a;
b=(height-1)/2;
d=b;
rad=pi/180*ang;
t1=[1 0 0;0 1 0;x y 1];
t2=[1 0 0;0 1 0;-a -b 1];
t3=[cos(rad) -sin(rad) 0;sin(rad) cos(rad) 0;0 0 1];
t4=[1 0 0;0 1 0;c d 1];
T=t2*t3*t4*t1;
tform=maketform('affine',T);
tx=zeros(width,height);
ty=zeros(width,height);
for i=1:width
for j=1:height
tx(i,j)=i;
end
end
for i=1:width
for j=1:height
ty(i,j)=j;
end
end
[w z]=tforminv(tform,tx,ty);
for i=1:width
for j=1:height
source_x=w(i,j);
source_y=z(i,j);
if(source_x>width-1||source_y>height-1||double(uint16(source_x))<=0||double(uint16(source_y))<=0)
new_J(i,j)=J(1,1);
else
if(source_x/double(uint16(source_x))==1.0&&(source_y/double(uint16(source_y)==1.0)))
new_J(i,j)=J(int16(source_x),int16(source_y));
else
a=double(uint16(source_x));
b=double(uint16(source_y));
x11=double(J(a,b));
x12=double(J(a,b+1));
x21=double(J(a+1,b));
x22=double(J(a+1,b+1));
new_J(i,j)=uint8((b+1-source_y)*((source_x-a)*x21+(a+1-source_x)*x11)+(source_y-b)*((source_x-a)*x22+(a+1-source_x)*x12));
end
end
end
end
J=new_J;
I=uint8(I);
J=uint8(J);
RegistrationImage=uint8(J);
%%%%%%%%%%%%%%%%%%%%%产生“融合”后的效果图%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
I=double(I)/255;
J=double(J)/255;
IJ=double(zeros(width,height));
for m=1:width
for n=1:height
if I(m,n)>0.999||J(m,n)>0.999
IJ(m,n)=0.8;
elseif I(m,n)==0||J(m,n)==0
IJ(m,n)=0.01;
else
IJ(m,n)=(I(m,n)*0.3+J(m,n)*0.7);
end
end
end
IJ=IJ*255;
IJ=uint8(IJ);
FusionImage=IJ;
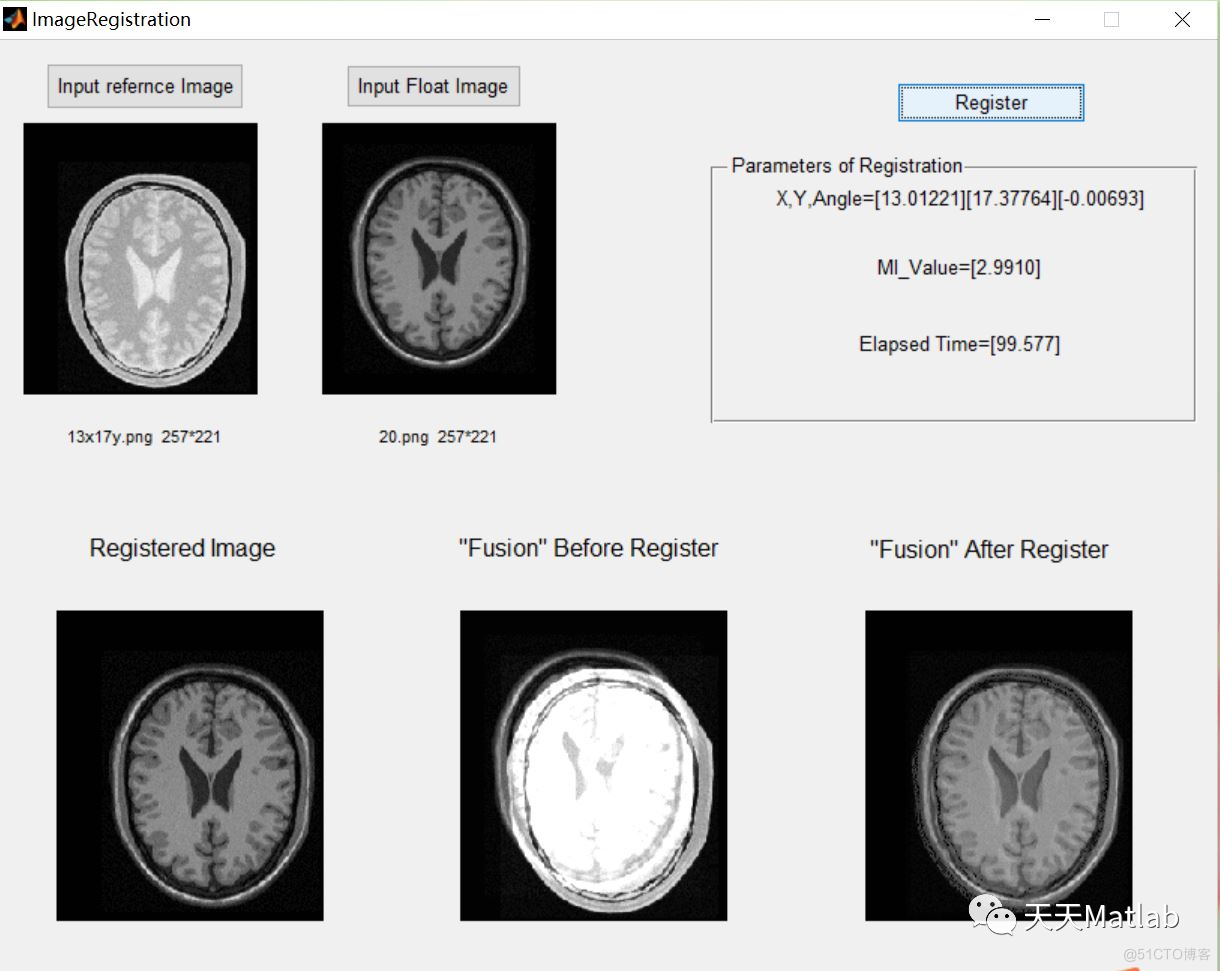
3 仿真结果
4 参考文献
[1]杨帆, 张汗灵. 蚁群算法和Powell法结合的多分辨率三维图像配准[J]. 电子与信息学报, 2007, 29(003):622-625.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

