BEGIN-3 圆的面积

资源限制

时间限制：1.0s 内存限制：256.0MB

问题描述

给定圆的半径r，求圆的面积。

输入格式

输入包含一个整数r，表示圆的半径。

输出格式

输出一行，包含一个实数，四舍五入保留小数点后7位，表示圆的面积。

说明：在本题中，输入是一个整数，但是输出是一个实数。

对于实数输出的问题，请一定看清楚实数输出的要求，比如本题中要求保留小数点后7位，则你的程序必须严格的输出7位小数，输出过多或者过少的小数位数都是不行的，都会被认为错误。

实数输出的问题如果没有特别说明，舍入都是按四舍五入进行。

样例输入

4

样例输出

50.2654825

数据规模与约定

1 <= r <= 10000。

​提示​

本题对精度要求较高，请注意π的值应该取较精确的值。你可以使用常量来表示π，比如PI=3.14159265358979323，也可以使用数学公式来求π，比如PI=atan(1.0)*4。

Code

Python

import math


r = int(input())
area = math.pi * r * r
print("%.7f" % area)

这里有一个小坑，取小数点后七位数字，用round()函数就不行。

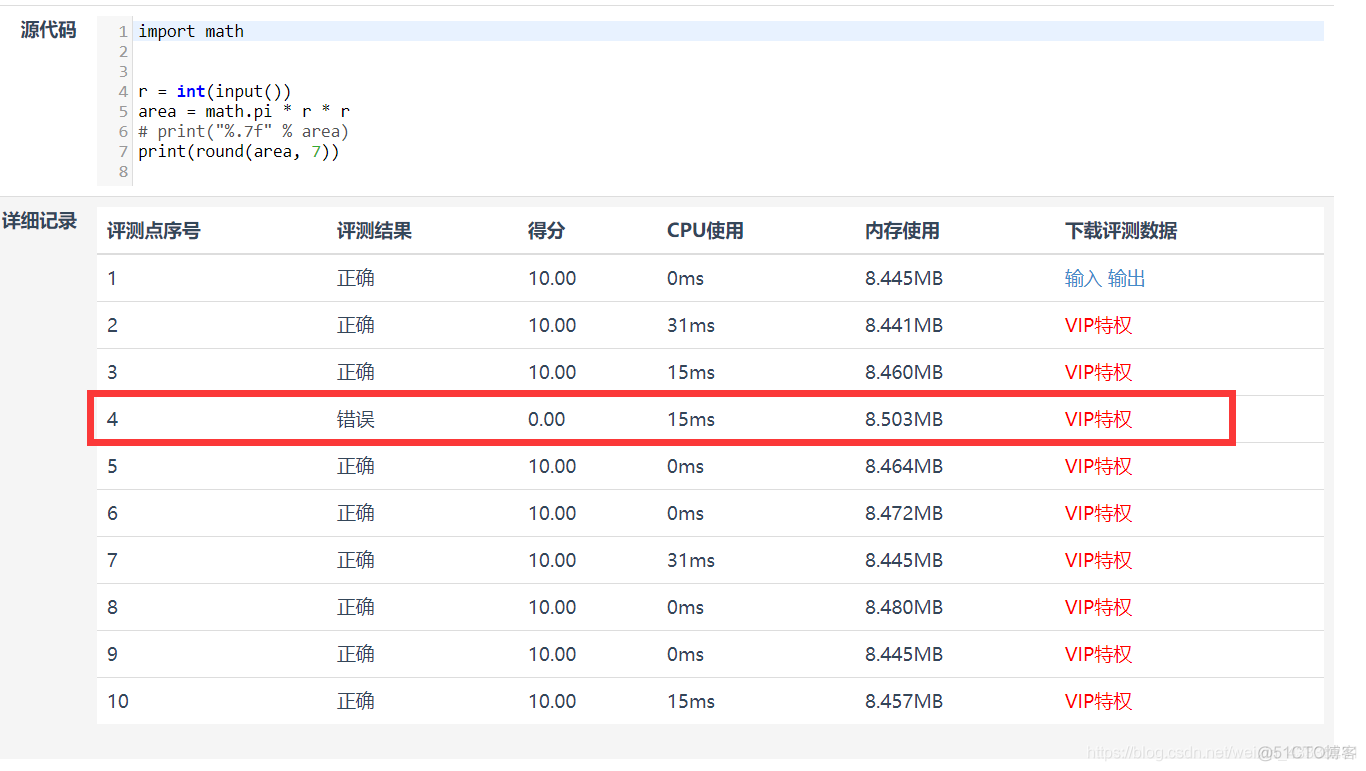
这道题比较简单，我们可以做一个对数器检验一下：

import math


if __name__ == '__main__':
for r in range(1000):
area = math.pi * r * r
if str(round(area, 7)) != "%.7f" % area:
print(str(round(area, 7)))
print("%.7f" % area)
break

这一试就试出来结果了：

0.0
0.0000000

现在我们就知道了，round()函数会对后缀零做截断处理，比如说：

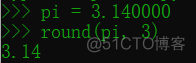
对3.140000取小数点后三位的时候只会保留3.14，舍去最后的零。

round()函数小坑

​1、round的结果跟python版本有关​

来看看python2和python3中round()函数有什么不同：

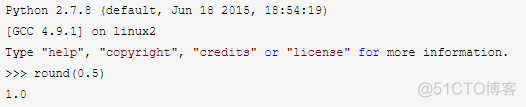
在python2.7的doc中，round()的最后写着，“Values are rounded to the closest multiple of 10 to the power minus ndigits; if two multiples are equally close, rounding is done away from 0.”

保留值将保留到离上一位更近的一端（四舍六入），如果距离两端一样远，则保留到离0远的一边。

所以round(0.5)会近似到1，而round(-0.5)会近似到-1。

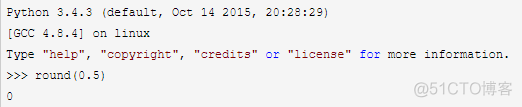
但是到了python3.5的doc中，文档变成了“values are rounded to the closest multiple of 10 to the power minus ndigits; if two multiples are equally close, rounding is done toward the even choice.”

如果距离两边一样远，会保留到偶数的一边。

比如round(0.5)和round(-0.5)都会保留到0，而round(1.5)会保留到2。

​2、特殊数字round出来的结果可能未必是想要的​

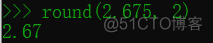
round(2.675, 2) 的结果，不论我们从python2还是3来看，结果都应该是2.68的，结果它偏偏是2.67，为什么？

这跟浮点数的精度有关。

我们知道在机器中浮点数不一定能精确表达，因为换算成一串1和0后可能是无限位数的，机器已经做出了截断处理。

那么在机器中保存的2.675这个数字就比实际数字要小那么一点点。

这一点点就导致了它离2.67要更近一点点，所以保留两位小数时就近似到了2.67。

​除非对精确度没什么要求，否则尽量避开用round()函数。​

近似计算我们还有其他的选择：

使用math模块中的一些函数，比如math.ceiling（天花板除法）。

python自带整除，python2中是/，3中是//，还有div函数。

字符串格式化可以做截断使用。

当然，对浮点数精度要求如果很高的话，请用decimal模块。