【SVM预测】基于引力搜索算法改进SVM实现数据回归预测Matlab代码

1 简介

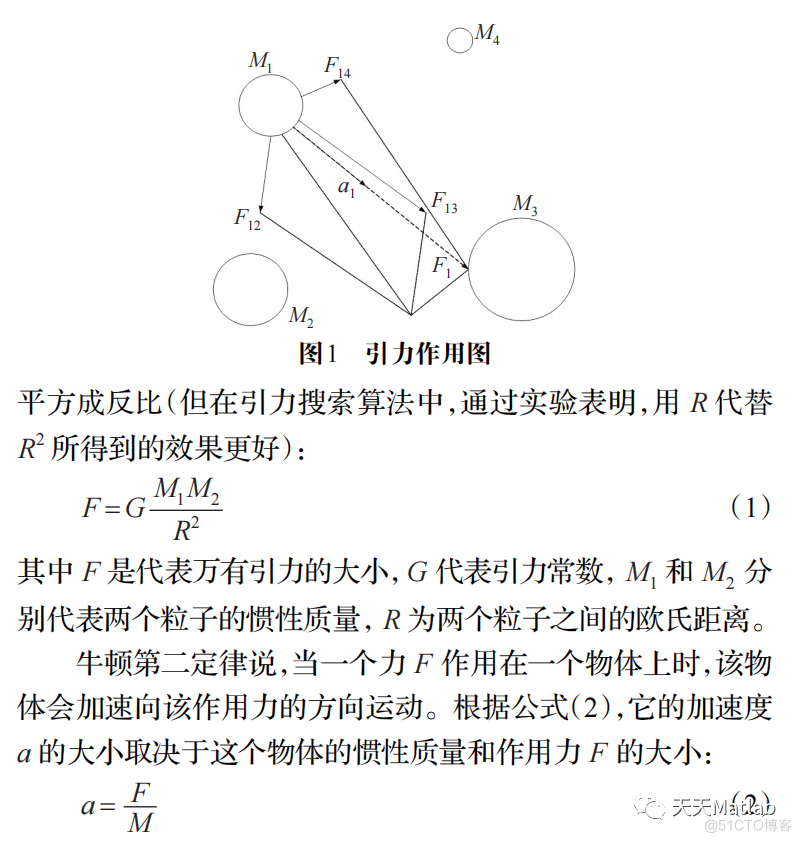
为了提高支持向量机(SVM)模型的拟合精度和泛化能力,以最小化输出量的均方误差为目标,采用基于万有引力定律的优化机制,提出了一种基于引力搜索算法的SVM参数优化方法.通过仿真实验验证,基于引力搜索算法的SVM回归模型不但精度高且泛化能力强.将该方法应用于谷氨酸发酵过程的建模研究,仿真结果表明,该方法可以提高谷氨酸质量浓度的预测精度.

2 部分代码

% GSA code v1.0.
% Generated by Esmat Rashedi, 2009.
% Adopted from: " E. Rashedi, H. Nezamabadi-pour and S. Saryazdi,
% 揋SA: A Gravitational Search Algorithm? Information sciences, vol. 179,
% no. 13, pp. 2232-2248, 2009."
% Gravitational Search Algorithm.
function BestChart=GSA(F_index,N,max_it,ElitistCheck,chaosIndex,chValueInitial)
%V: Velocity.
%a: Acceleration.
%M: Mass. Ma=Mp=Mi=M;
%dim: Dimension of test function.
%N: Number of agents.
%X: Position of agents. dim-by-N matrix.
%R: Distance between agents in search space.
%[low-up]: Allowable range for search space.
%Rnorm: Norm in eq.8.
%Rpower: Power of R in eq.7.
G_History=zeros(1,max_it);
Rnorm=2;
Rpower=1;
min_flag=1; % 1: minimization, 0: maximization
%get allowable range and dimension of the test function.
[low,up,dim]=test_functions_range(F_index);
%random initialization for agents.
X=initialization(dim,N,up,low);
%create chart of best so far and average fitnesses.
BestChart=[];MeanChart=[];
V=zeros(dim,N);
wMax=chValueInitial;
wMin=1e-10;
for iteration=1:max_it
chValue=wMax-iteration*((wMax-wMin)/max_it);
% iteration
%Checking allowable range.
X=space_bound(X,up,low);
%Evaluation of agents.
fitness=evaluateF(X,F_index);
[best best_X]=min(fitness); %min: minimization. max: maximization.
if iteration==1
Fbest=best;Lbest=X(:,best_X);
end
if best<Fbest % < : minimization. > : maximization
Fbest=best;Lbest=X(:,best_X);
end
BestChart=[BestChart Fbest];
MeanChart=[MeanChart mean(fitness)];
%Calculation of M. eq.14-20
[M]=massCalculation(fitness,min_flag);
%Calculation of Gravitational constant. eq.13.
G=Gconstant(iteration,max_it);
%G=chaos(3,iteration,max_it,10);
switch chaosIndex
case 1
G=Gconstant(iteration,max_it);
case 2
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 3
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 4
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 5
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 6
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 7
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 8
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 9
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 10
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
case 11
G=G+chaos(chaosIndex-1,iteration,max_it,chValue);
end
G_History(iteration)=G;
test_G(iteration)=G;
if iteration==499
alisop=0;
end
%Calculation of accelaration in gravitational field. eq.7-10,21.
a=Gfield(M,X,G,Rnorm,Rpower,ElitistCheck,iteration,max_it);
%Agent movement. eq.11-12
[X,V]=move(X,a,V);
end %iteration

3 仿真结果

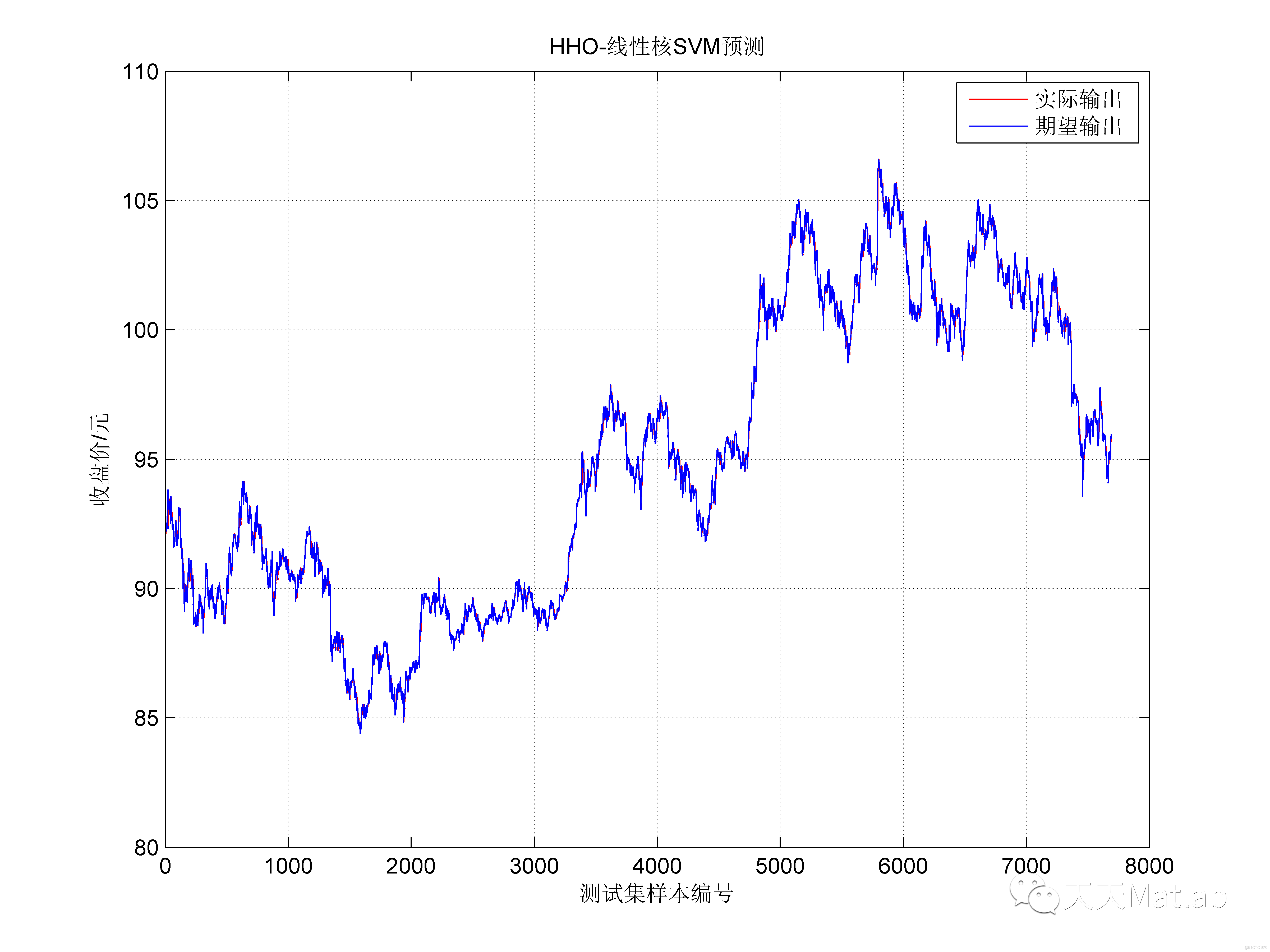
4 参考文献

[1]戴娟, 顾斌杰, 潘丰. 基于引力搜索算法的SVM参数优化及应用[J]. 服装学报, 2013, 12(002):127-131.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。