选择排序的简单理解

选择排序的概念非常容易理解，按照一般的思路，排序就是每次从原来的序列中拿出最小的元素即可，最终得到的序列就是有序序列。 详细描述

选择排序的工作原理是：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾，以此类推，直到全部待排序的数据元素的个数为零。

选择排序详细的执行步骤如下：

1. 初始状态：无序区为 R[1..n]，有序区为空；
2. 第 i 趟排序 (i=1,2,3…n-1) 开始时，当前有序区和无序区分别为 R[1...i-1] 和 R(i...n)。该趟排序从当前无序区中选出关键字最小的记录 R[k]，将它与无序区的第 1 个记录 R 交换，使 R[1...i] 和 R[i+1...n) 分别变为记录个数增加 1 个的新有序区和记录个数减少 1 个的新无序区；
3. 经过 n-1 趟，无序序列就有序化了。

算法图解

问题解疑 为什么选择排序是不稳定的？

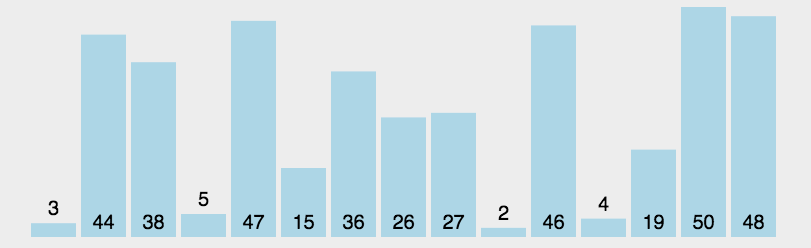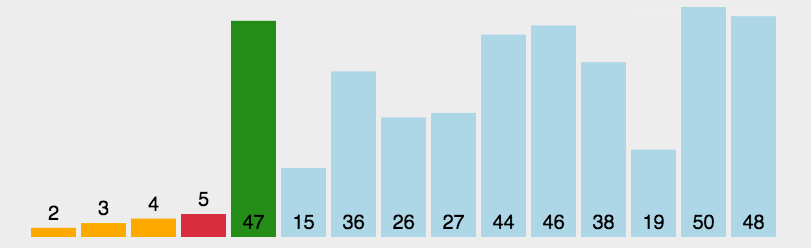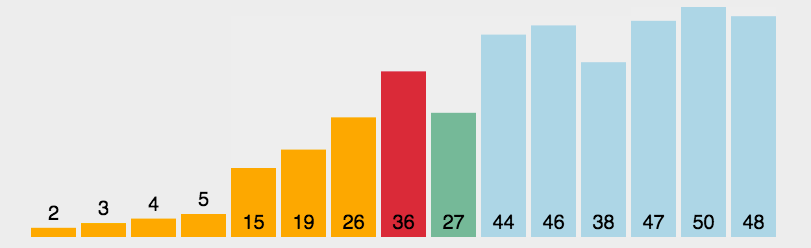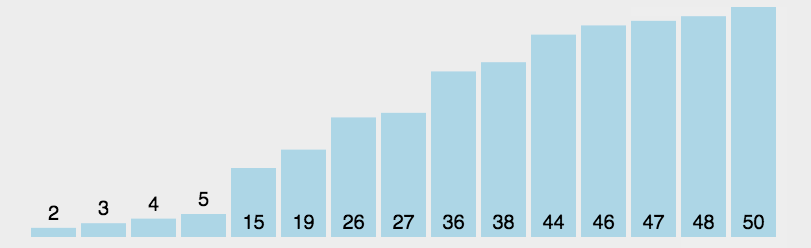
虽然原理上存在有序区和无序区的区分，但是选择排序算法为了提高空间的使用率，使用的是原地交换方式。

与冒泡排序两两比较交换不同，选择排序算法是最小的元素与固定位置的元素进行交换，当这个固定位置的元素被交换到另一个位置之后，也就有可能导致相等的数字次序变化。

选择排序的时间复杂度是多少？

无论原序列是有序还是无序，选择排序都需要对序列做完整的遍历，即最好情况时间复杂度和最坏情况时间复杂度都是 \(O(n^2)\)；平均时间复杂度是 \(O(n^2)\)。

代码实现

package cn.fatedeity.sort;

/**
 * 选择排序算法
 */
public class SelectionSort {
    private static void swap(int[] numbers, int src, int target) {
        int temp = numbers[src];
        numbers[src] = numbers[target];
        numbers[target] = temp;
    }

    public static int[] sort(int[] numbers) {
        for (int i = 0; i < numbers.length - 1; i++) {
            for (int j = i + 1; j < numbers.length; j++) {
                if (numbers[i] <= numbers[j]) {
                    continue;
                }
                swap(numbers, i, j);
            }
        }
        return numbers;
    }
}

首发于翔仔的个人博客，点击查看更多。