1. 基本常识
1.1 什么是栈
我们用一种最简单的生活常识描述一下,比如我们往柜子里放东西,先放的东西是需要放到柜子最里边,后放的东西在柜子的最外边;如果我们要取东西,先要取柜子最外边的东西,才能取到柜子最里边的东西。这种先进后出,后进先出的结构称为“栈”。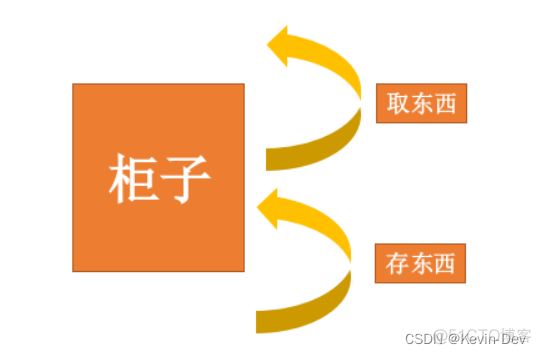
1.2 栈的特点
“先进后出,后进先出”。
1.3 栈的操作
栈的操作就两种,分别为出栈和入栈。那我们上边的例子,我们往柜子里放东西的过程称为入栈;我们在柜子里拿东西的过程称为出栈。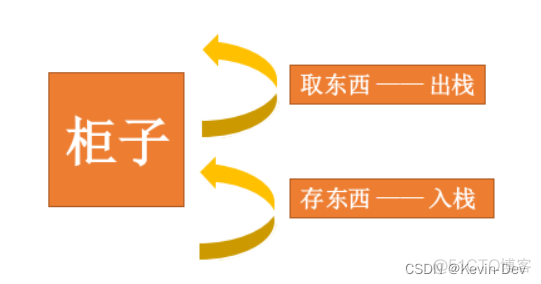
2. 栈的实现
所有的数据结构基本都是由数组和链表演化而来的,所以今天讲的栈这种数据结构也不例外。
栈的实现主要有两种,一种是数组的实现,叫做顺序栈,另外一种是链表的实现,叫做链式栈。
2.1 顺序栈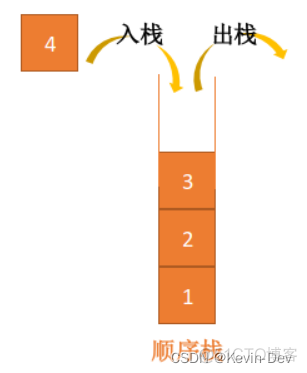
2.2 链表栈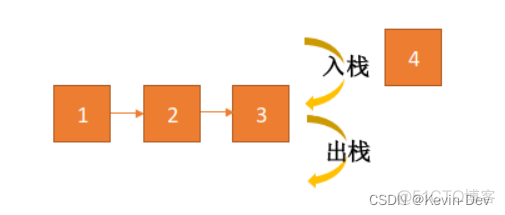
2.3 代码实现
顺序栈
* 功能:基于数组的顺序栈
* 公众号:一个不甘平凡的码农
* @author:小鹿
*
*/
public class ArrayStack {
private String[] items; // 数组
private int count; // 栈中元素个数
private int n; // 栈的大小
// 初始化数组,申请一个大小为 n 的数组空间
public ArrayStack(int n) {
this.items = new String[n];
this.n = n;
this.count = 0;
}
/**
* 功能:入栈
* 说明:数组入栈的入口为数组尾部
* @param item :入栈数据元素
* @return:是否入栈成功
*/
public boolean push(String item) {
// 数组空间不够了,直接返回 false,入栈失败。
if (count == n) return false;
// 将 item 放到下标为 count 的位置
items[count] = item;
//数组长度+1
++count;
//入栈成功
return true;
}
/**
* 功能:出栈
*
* @return:返回出栈元素
*/
public String pop() {
// 栈为空,则直接返回 null
if (count == 0) return null;
// 返回下标为 count-1 的数组元素
String tmp = items[count-1];
//数组长度-1
--count;
//返回出栈数据元素
return tmp;
}
}
链式栈
/*** 功能:基本链表的链式栈,入栈、出栈、输出栈
* @author : 小鹿
* 公众号:一个不甘平凡的码农
*/
public class StackBasedLinkedList {
//定义栈顶指针
private Node top = null;
//定义栈结点
private static class Node {
//栈结点数据域
private int data;
//栈结点指针域
private Node next;
//构造函数
public Node(int data, Node next) {
this.data = data;
this.next = next;
}
//get 获取数据域方法
public int getData() {
return data;
}
}
/**
* 功能:入栈
* @param value:要入栈的数据元素
*/
public void push(int value) {
//创建一个栈结点
Node newNode = new Node(value, null);
// 判断栈是否为空
if (top == null) {
//如果栈为空,就将入栈的值作为栈的第一个元素
top = newNode;
} else {
//否则插入到top栈结点前(所谓的就是单链表的头插法)
newNode.next = top;
top = newNode;
}
}
/**
* 功能 : 出栈
* @return: -1 为栈中没有数据
*/
public int pop() {
// 如果栈的最顶层栈结点为null,栈为空
if (top == null) return -1;
//否则执行出栈操作,现将栈顶结点的数据元素赋值给 Value
int value = top.data;
//将 top 指针向下移动
top = top.next;
//返回出栈的值
return value;
}
/**
* 功能:输出栈中所有元素
*/
public void printAll() {
//将栈顶指针赋值给p
Node p = top;
//循环遍历栈(遍历单链表)
while (p != null) {
System.out.print(p.data + " ");
//指向下一个结点
p = p.next;
}
System.out.println();
}
}
3. 栈的性能
3.1 时间复杂度
时间上的消耗主要分析栈的操作所消耗的时间,我们共两种操作,入栈和出栈,其实在数组中中,我们操作尾部的数据就相当于入栈和出栈,直接根据下标取得相应的元素就好(JS 中数组的 pop 和 push 方法),所以时间复杂度是 O(1)。
3.2 空间复杂度
空间复杂度的判断是所需要开辟的临时空间,顺序栈和链式栈只需要大小为 n 的空间就可以,入栈和出栈需要一个临时空间来存储变量,空间复杂度为 O(1)。
3.3 栈的动态扩容
大家有没有想过这样一种情况,如果栈满的时候,再进行入栈操作,栈内就放不下了,我们需要动态扩容。主要是顺序栈的动态扩容比较麻烦,和我么你之前的数组的文章动态扩容一样的,对于动态扩容的性能,可以自己尝试一下。
4. 栈的实际应用
既然我们把栈的性能分析透了,理解透了,那么我们看看栈在实际中有哪些应用吧。
4.1 应用一 :栈在函数中的应用
函数我们每个人再熟悉不过了,你是不是很纳闷,栈怎么会在函数中能够应用的到呢,我学了这几年函数,我咋不知道函数中还有栈的操作。
加入我们程序开始执行代码,执行到我们声明的函数时,计算机内部会发生什么呢?首先,会为该函数开辟一块临时的内存空间,这块内存空被组织成“栈”这种数据结构,作用主要用来存储函数内部声明的临时变量。
每执行一个函数,系统就将函数中的临时变量组织成栈帧,执行入栈操作,当函数被调用完成的时候,临时变量已经用不到了,所以要在内存中释放,执行出栈操作。如以下函数:
function main(){let i = 0;
let j = 1;
i++;
j++;
console.log(i+j)
}
main();
具体如下: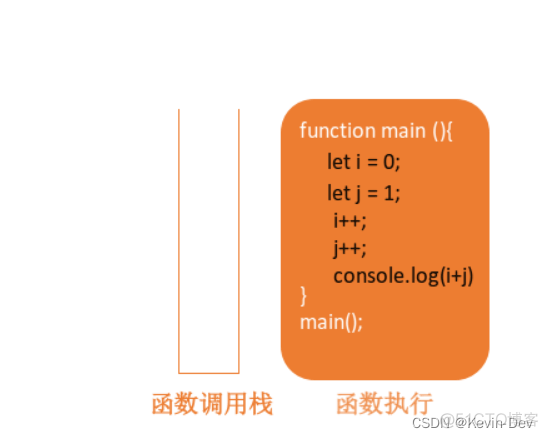
我们这时要想一个问题,那为什么函数会使用栈这种数据结构呢,为什么不用队列、链表或者其他数据结构?全体注意,重点来了,以后分析其他的问题也用到一下的方法分析。
因为函数调用的执行顺序符合后进者先出,先进者后出的特点。
比如函数中的局部变量声明的时间顺序,早先定义的变量在内存中保存的时间长,后定义的变量在内存中保存的时间短,所有有一个先后的问题。我们再去脑海中把这种问题的特点抽象成数据结构,只有使用“栈”结构,才符合这种问题。
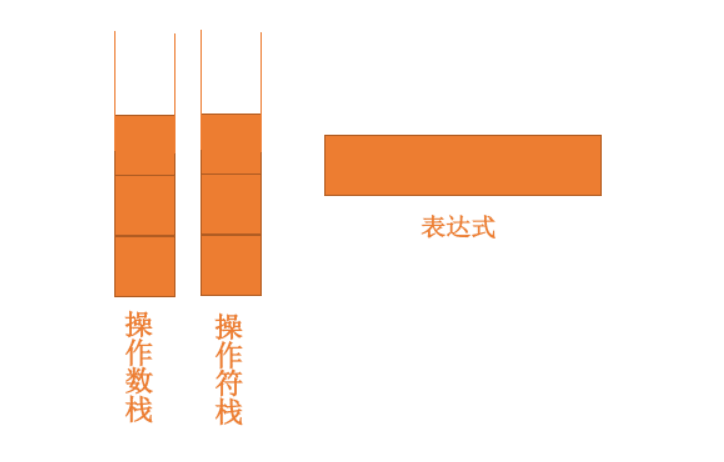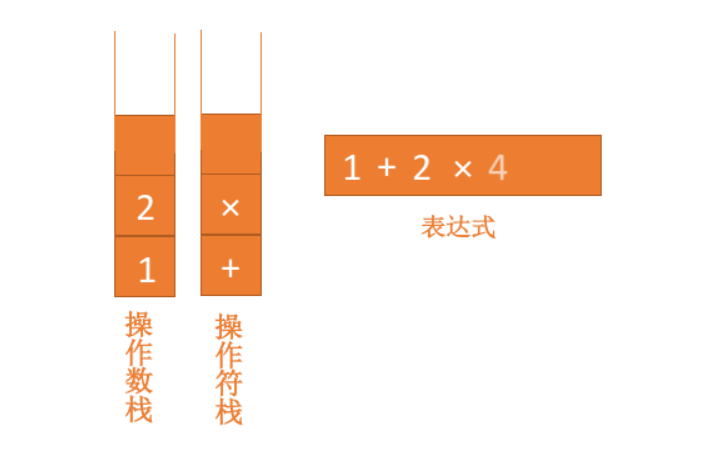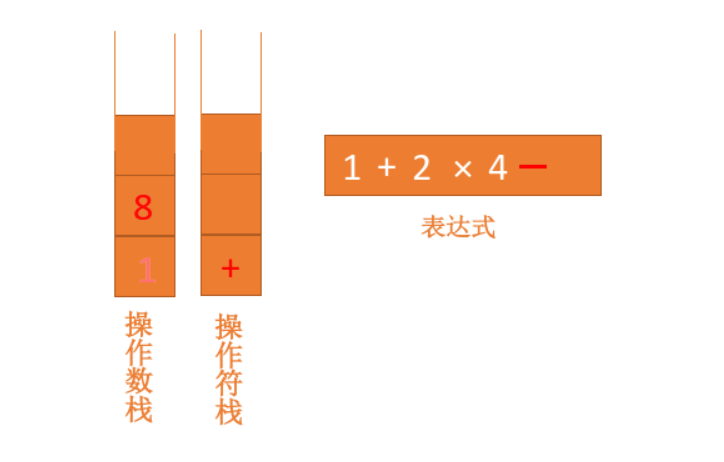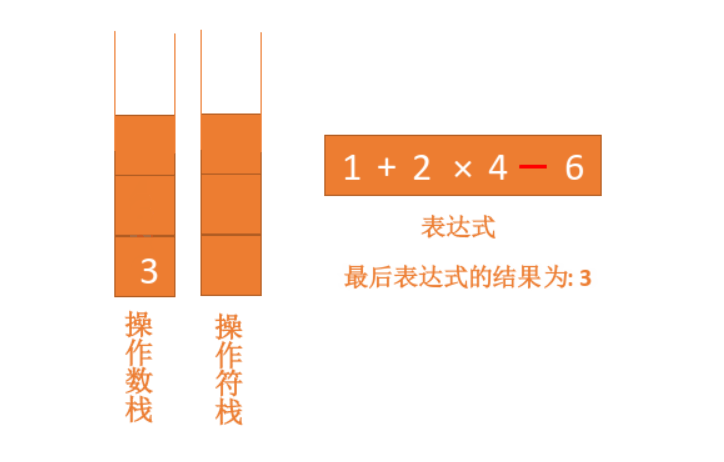
4.2 栈在表达式中应用
计算机中数字的运算也是使用栈这种数据结构的,我们举个例子,我们要计算如下表达式:
1 + 2 × 4 - 6
如果比运算符栈顶元素的优先级高,就将当前运算符压入栈;如果比运算符栈顶元素的优先级低或者相同,从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算完的结果压入操作数栈,继续比较。动画如下: