使用scikit-learn对数据进行预处理

数据的质量决定了模型的上限，在真实的数据分析中，输入的数据会存在缺失值，不同特征的取值范围差异过大等问题，所以首先需要对数据进行预处理。

预处理是数据挖掘的第一步，该步骤实际上包含了很多不同的操作手法，大致分为以下几类

1. 缺失值的处理，当样本量很大，缺失值很少时，直接删除缺失值对应的样本，并不会导致样本规模的大幅下降，此时直接删除缺失值是一种可取的办法，但是对于小样本量，且缺失值较多的场景，就需要考虑对缺失值进行插补

2. 标准化，很多的机器学习算法对特征的分布是有预定的假设的，比如需要服从正态分布，对于不符合分布的数据，需要进行标准化，转化为正态分布，另外，考虑到不同特征的量纲不同，也需要进行缩放，比如到缩放到0到1的区间，保证了不同特征在模型中的可比性

3. 稀疏化，也叫做离散化，指的是根据业务场景对特征进行分段处理，比如按照某个阈值，将考试分数划分为及格和不及格两类，从而将连续性的数值变换为0,1两个离散型的变量

4. 特征编码，对于分类变量，近期映射为数值型

5. 特征提取，适用于自然语言处理，图形识别领域的机器学习，因为原始的数据数据是文本，图像等数据，不能直接用于建模，所以需要通过特征提取转换为适合建模的矩阵数据

在scikit-learn中，在preprocessing子模块中提供了多种预处理的方法，具体用法如下

1. 标准化

标准化的目标是使得变量服从标准正态分布，标准化的方式如下

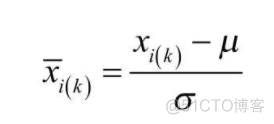
代码如下

>>> from sklearn import preprocessing
>>> import numpy as np
>>> x = np.array([1, -2, 3, -4, 5, 6]).reshape(-1, 1)
>>> x
array([[ 1],
[-2],
[ 3],
[-4],
[ 5],
[ 6]])
>>> scaler = preprocessing.StandardScaler().fit(x)
>>> x_scaled = scaler.transform(x)
>>> x_scaled
array([[-0.13912167],
[-0.97385168],
[ 0.41736501],
[-1.53033836],
[ 0.97385168],
[ 1.25209502]])
```

2.  线性缩放

适合针对标准差很小的数据集进行处理，根据数据的最大值和最小值，将原始数据缩放到0到1这个区间代码如下

>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> x_scaled = min_max_scaler.fit_transform(x)
>>> x_scaled
array([[0.5],
[0.2],
[0.7],
[0. ],
[0.9],
[1. ]])

也可以通过feature_range参数设定具体的缩放区间

>>> min_max_scaler = preprocessing.MinMaxScaler(feature_range=(-5, 5))
>>> x_scaled = min_max_scaler.fit_transform(x)
>>> x_scaled
array([[ 0.],
[-3.],
[ 2.],
[-5.],
[ 4.],
[ 5.]])

还有一种方法是根据最大绝对值进行缩放，适合稀疏数据或者是早已经中心化的数据，可以缩放到-1到1的区间，代码如下

>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> x_scaled = max_abs_scaler.fit_transform(x)
>>> x_scaled
array([[ 0.16666667],
[-0.33333333],
[ 0.5 ],
[-0.66666667],
[ 0.83333333],
[ 1. ]])

3. 非线性变换

包括分位数变换和幂变换两种，分位数变换，默认对样本量大于1000的数据进行变化，采用分位数对原始数据划分，默认将数据映射为0到1的均匀分布，代码如下

>>> x = np.random.random(10000).reshape(-1, 1)
>>> x_scaled = quantile_transformer.fit_transform(x)

也可以输出符合正态分布的数据，代码如下

>>> quantile_transformer = preprocessing.QuantileTransformer(output_distribution='normal')
>>> x_scaled = quantile_transformer.fit_transform(x)

幂变换，用于稳定方差，将数据处理为近似正态分布，代码如下

>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> x_scaled = pt.fit_transform(x)

4. 正则化

代码如下

>>> x_normalized = preprocessing.normalize(x, norm='l2')
>>> x_normalized = preprocessing.Normalizer(norm='l2').fit_transform(x)

5.  特征编码

将离散的分类型变量转换为数值型，代码如下

>>> x = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> preprocessing.OrdinalEncoder().fit_transform(x)
array([[1., 1., 1.],
[0., 0., 0.]])

6. 离散化

将连续变量进行分组，比如将原始数据划分为不同的区间，称之为bin, 代码如下

>>> X = np.array([[ -3., 5., 15 ],[ 0., 6., 14 ],[ 6., 3., 11 ]])
>>> X
array([[-3., 5., 15.],
[ 0., 6., 14.],
[ 6., 3., 11.]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)
>>> est.transform(X)
array([[0., 1., 1.],
[1., 1., 1.],
[2., 0., 0.]])

n_bins参数指定bin的个数，转换后的数值为原始数值对应的bin的下标。

二值化变换，也是一种离散化的操作，通过某个阈值将数值划分为0和1两类，公式如下

代码如下

>>> X = np.array([[ 1., -1., 2.],[ 2., 0., 0.],[ 0., 1., -1.]])
>>> X
array([[ 1., -1., 2.],
[ 2., 0., 0.],
[ 0., 1., -1.]])
>>> binarizer = preprocessing.Binarizer(threshold=1.1).fit(X)
>>> binarizer.transform(X)
array([[0., 0., 1.],
[1., 0., 0.],
[0., 0., 0.]])

7.  多项式构建

多项式的构建相当于升维操作，在原来独立的特征x1, x2的基础上，构建起平方以及乘积的新变量，转换到方式如下

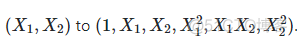
代码如下

>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures().fit_transform(X)
>>> poly
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])

8. 自定义

为了提供更加灵活的预处理方式，还支持自定义预处理的逻辑，代码如下

>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> trans = transformer.fit_transform(X)
>>> trans
array([[0. , 0.69314718],
[1.09861229, 1.38629436]])

通过自定义函数来保证灵活性。对于缺失值的填充，有专门的impute子模块来进行处理，在后续的文章中再详细介绍。

·end·

一个只分享干货的

生信公众号