深入了解MySQL索引结构

本篇文章给大家带来了关于mysql的相关知识，其中主要介绍了关于索引结构的相关问题，那么，索引的结构是什么样的？为什么索引可以这么快？下面一起来看一下吧，希望对大家有帮助。

推荐学习：mysql教程

数据库存储单位

首先我们要知道，由于为了实现持久化，只能将索引存储在硬盘上，通过索引来进行查询的时候就会产生硬盘的 I/O 操作，因此，设计索引时需要尽可能的减少查找次数，从而减少 I/O 耗时。

此外还需要知道一个很重要的原理：数据库管理存储空间的基本单位是页(Page)，一个页中存储多条行记录(Row)。

计算机系统对磁盘 I/O 会做预读优化，当一次I/O时，除了当前磁盘地址的数据以外，还会把相邻的数据也读取到内存缓冲池中，每一次 I/O 读取的数据成为一页，InnoDB 默认的页大小是 16KB。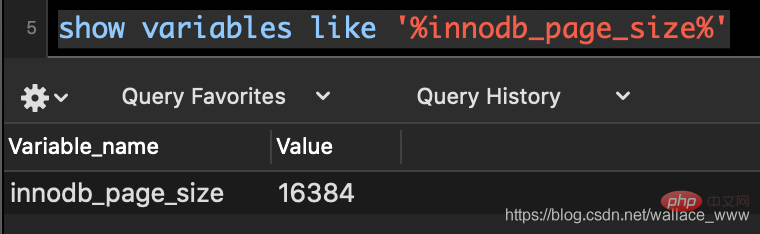
连续的 64 个页组成一个区(Extent)，一个或多个区组成一个段(Segment)，一个或多个段组成表空间(Tablespace)。InnoDB 有两种表空间类型，共享表空间表示多张表共享一个表空间，独立表空间表示每张表的数据和索引全部存在独立的表空间中。

数据页结构如下（图源：极客时间《MySQL 必知必会》）：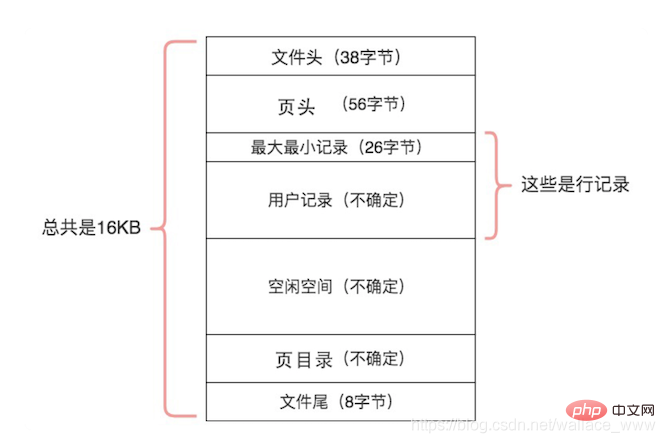

数据页的 7 个结构内容可以大致分为以下三类：

• 文件通用部分，用于校验页传输完整
  • 文件头（File Header）: 表述页信息，文件头中使用 FIL_PAGE_PREV 和 FIL_PAGE_NEXT 构成一个双向链表，分别指向前后的数据页。
  • 页头（File Header）：记录页的状态信息
  • 文件尾（File Trailer）: 校验页是否完整
• 记录部分，用于存储数据记录
  • 最大最小记录（Infimum/Supremum）：虚拟的行记录，表示数据页的最大记录和最小记录。
  • 用户记录（User Record）和空闲空间（Free Space）: 用于存储数据行记录内容
• 索引部分，用于提高记录的检索效率
  • 页目录（Page Directory）：存储用户记录的相对位置

详情可参考淘宝的数据库内核月报

索引数据结构

很自然的，我们会想到查找算法中涉及到的一些常用数据结构，比如二叉查找树，二叉平衡树等等，实际上，Innodb 的索引是用 B+ 树 来实现的，下面我们来看看为何会选择这种索引结构。

二叉树的局限性

先来简单回顾一下二叉搜索树（Binary Search Tree）的定义，二叉搜索树中，如果要查找的 key 大于根节点，则在右子树中搜索，如果 key 小于根节点，则在左子树中搜索，直到找到 key 为止，时间复杂度为 O(logn)。比如数列 [4,2,6,1,3,5,7]，会生成如下二叉搜索树：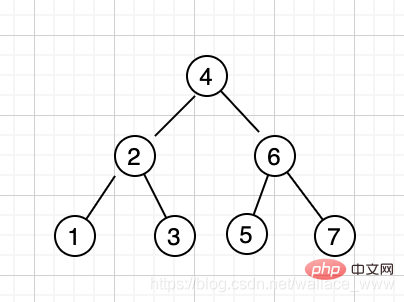

但是在某些特殊情况下，二叉树的深度会非常大，比如 [1,2,3,4,5,6,7]，则会生成如下的树：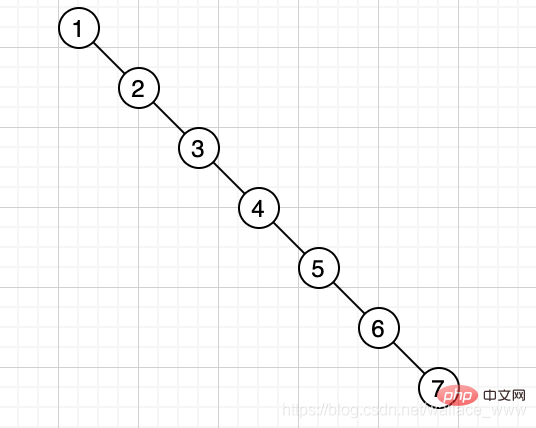

在下面这种情况中，最坏的情况下需要查 7 次才能够查到想要的结果，查询时间变成了 O(n)。

为了优化这种情况，就有了平衡二叉搜索树（AVL 树），AVL 树是指左右子树的高度相差不超过 1 的树，搜索时间复杂度为 O(logn)，这已经是比较理想的搜索树了，但是在动辄几千万行记录的数据库中，树的深度还是会很高，依然不是最理想的结构。

B 树

那么，如果从二叉树扩展到 N 叉树呢，很容易想象到，N 叉树可以大大的减少树的深度，实际上，4 层树结构就已经可以支撑几十 T 的数据了。

B 树（Balance Tree）就是这样的一种 N 叉树， B 树也称为 B- 树，满足如下定义：
设 k 为 B 树的度 (degree, 表示每个节点最多能有多少个子节点)，

1. 每个磁盘块中最多包含 k - 1 个关键字 和 k 个子节点的指针
2. 叶子节点中，只有关键字，没有子节点指针
3. 每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
4. 所有叶子节点位于同一层。

上面已经提到，每一次 I/O 会预读一个磁盘块的数据，大小为一页，用一个磁盘块的内容表示一次 I/O，B 树的结构如下图 (图源：极客时间 SQL 必知必会)：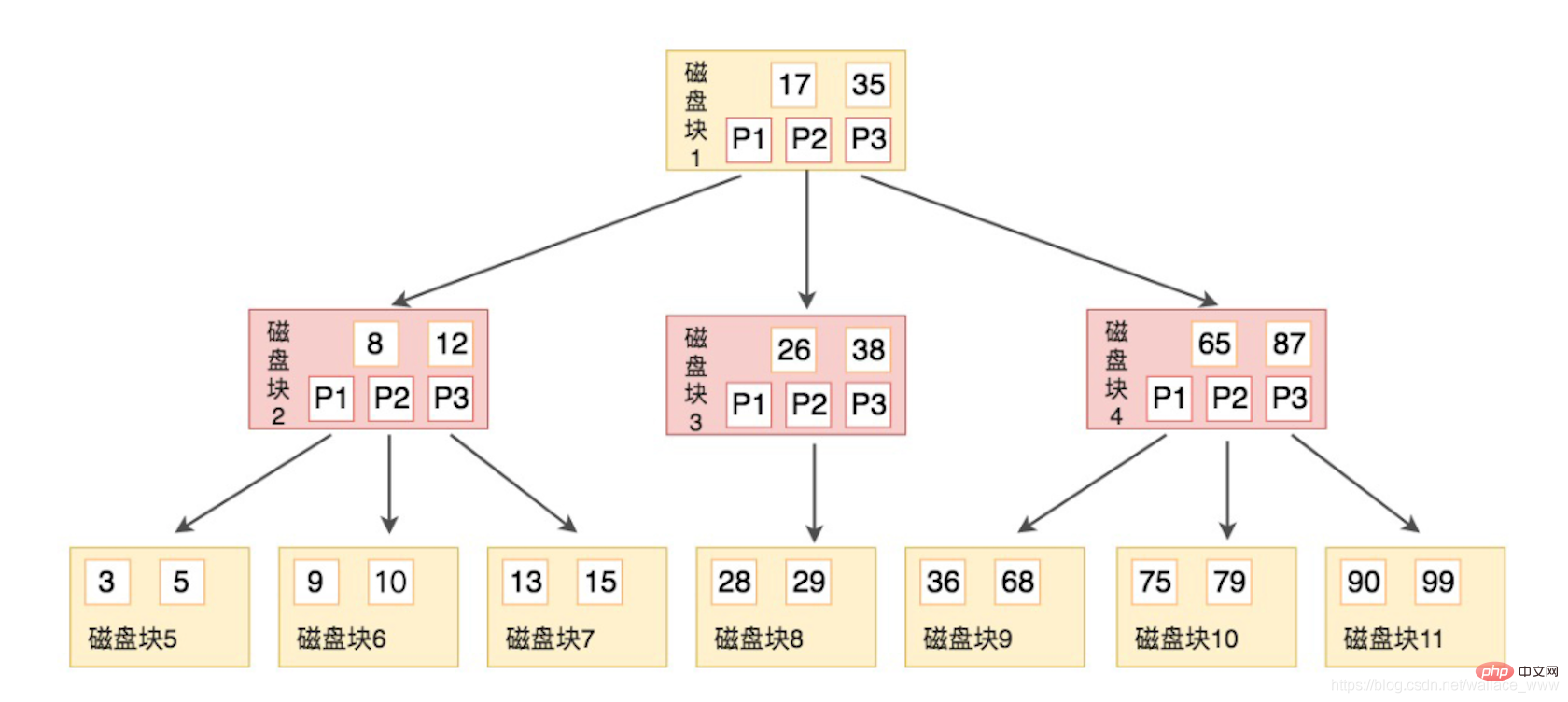

B 树也是有序的，由于子节点指针一定比关键字多 1，所以正好可以用关键字划分子节点的区段，如图中的例子，每个节点有 2 个关键字，3 个子节点，如磁盘块 2 ，第一个字节点的关键字 3，5 小于自身的第一个子节点 8，第二个子节点的 9，10 在 8 和 12 之间，第三个子节点的值 13，15 大于自身的第二个子节点 12。

假设我们现在要查找 9，步骤如下：

1. 与根节点磁盘块 1 (17,35) 比较，小于 17，继续在指针 P1 中查找，对应磁盘块 2
2. 与磁盘块 2 (8,12) 比较，位于两者之间，继续在指针 P2 查找，对应磁盘块 6
3. 与磁盘块 6 (9, 10) 比较，找到 9

可以看到，虽然做了很多次比较的操作，但是由于进行了预读，所以在磁盘块内部的比较是在内存中进行的，不耗费磁盘 I/O，上述操作只需要进行 3 次 I/O 即可完成，已经是比较理想的结构了。

B+ 树索引

B+ 树在 B 树的基础上进行了进一步的改进，B+ 树和 B 树的区别有以下几点：

1. B+ 树的构建方式是，对于父节点中的关键字，左子树的所有关键字小于它，右子树的所有关键字都大于等于它
2. 非叶子节点仅用于索引，不会存储数据记录
3. 父节点的关键字也会出现在子节点中，并且都是子节点中的最大值（或者最小值）
4. 所有关键字都会出现在叶子节点中，叶子节点构成一个有序链表，按从小到大排序。

示例如下，本例中，父节点的关键字都是子节点中的最小值 (图源：极客时间 SQL 必知必会)：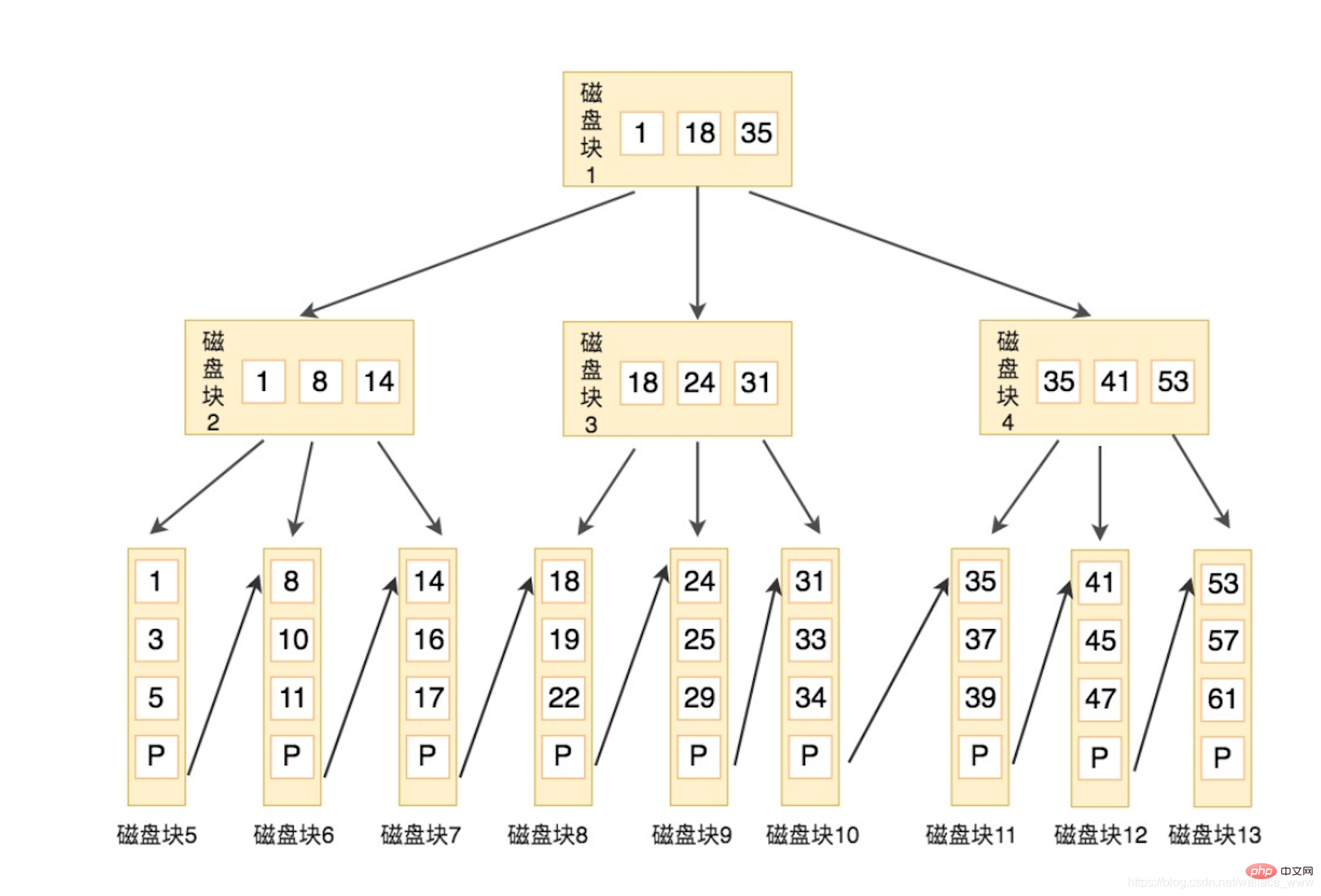
假设要查找关键字 16，查找步骤如下：

1. 与根节点磁盘 1 (1,18,35) 比较，16 在 1 和 18 之间，得到指针 P1，指向磁盘 2
2. 找到磁盘 2 (1,8,14)，16 大于 14，得到指针P3，指向磁盘 7
3. 找到磁盘 7 (14,16,17)，找到16

B+ 树优点：

1. 内部节点不存储数据，因此每个内部节点可以存储的记录数量远大于 B树，树的高度更低，I/O 更少，每次 I/O 读取的数据页里内容更多
2. 可以支持范围查询，直接在叶子节点组成的有序链表遍历即可
3. 所有数据都存储在叶子节点，因此查询效率更稳定

HASH 索引

MySQL 的 memory 存储引擎默认的索引结构是 Hash 索引，Hash 是一种函数， 称为散列函数，通过特定算法（如 MD5, SHA1，SHA2 等）将任意长度的输入转换为固定长度的输出，输入和输出一一对应，本文不会对 hash 函数做深入的介绍，详情请参考 百度百科。

Hash 查找的效率为 O(1)，效率非常高，python 的 dict，golang 中的 map，java 中的 hash map 都是基于 hash 实现的，在 Redis 这样的 Key-Value 数据库也是由 Hash 实现。

对于精确查找而言，Hash 索引的效率会比 B+ 树索引更高，但是 Hash 索引有一些局限性，因此不是最主流的索引结构。

1. 因为 Hash 索引指向的数据是无序的，所以Hash 索引不能范围查询，也不支持 ORDER BY 排序。
2. 由于 Hash 是精确匹配，因此也不能进行模糊查询。
3. Hash 索引不支持联合索引的最左匹配原则，联合索引只有在完全匹配时生效。因为 Hash 索引计算 Hash 值的时候是将索引合并后再一起计算 Hash 值，而不会计算每个索引的单独 Hash 值。
4. 如果被索引字段的重复值很多，那就会造成大量的 Hash 冲突，这时候查询就会变得非常耗时。

基于上述原因考虑，Mysql InnoDB 引擎不支持 Hash 索引，但是在内存结构中有一个自适应 Hash 索引的功能，当某个索引值使用非常频繁的时候，会在 B+ 树索引的基础上自动创建一个 Hash 索引，来提高查询性能。

自适应 Hash 索引可以理解为一种 “索引的索引”，采用 Hash 索引储存 B+ 树索引中的页面地址，迅速定位到对应的叶子节点。可以通过 innodb_adaptive_hash_index 变量来查看。

推荐学习：mysql教程

以上就是深入了解MySQL索引结构的详细内容，更多请关注自由互联其它相关文章！