参考:https://www.zhihu.com/question/40049682/answer/1420483558 分两种情况: 一、 行 X 列 就是它长度的平方。 二、 列 X 行 通常对它进行一下处理(归一化 ): 对任意一个向量 b , 它投影到 a 上
参考:https://www.zhihu.com/question/40049682/answer/1420483558
分两种情况:
一、行 X 列
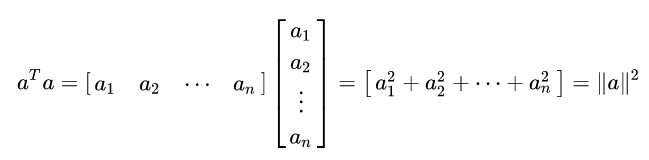
就是它长度的平方。
二、列 X 行

通常对它进行一下处理(归一化):
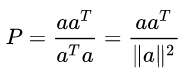
对任意一个向量 b , 它投影到 a 上的向量一定是:

--------------------------------------------------------------------------------------------------------------------------------
关于列 X 行 的投影的证明:
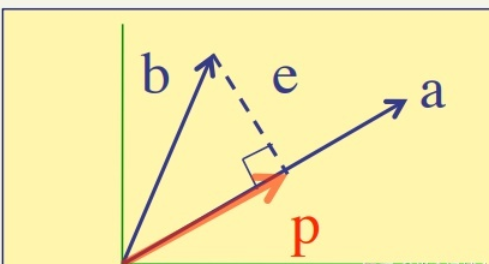
有两个向量 ![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
这个过程显然是一个线性变换,那么我们把这个线性变换记作: ![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
那么根据它的定义有:
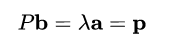
这里 ![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
从三角形法则考虑
向量 ![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
![[公式]](http://img.558idc.com/uploadfile/allimg/boke/equation)
那么转化为数量关系就有
再由标红的等量关系不难得出:
注意这时向量都默认为列向量,所以标量可以直接写成:
这就是上面提到的投影矩阵的全部证明过程了。
