1、对范数的理解

转载自：https://www.zhihu.com/question/20473040/answer/102907063

https://blog.csdn.net/yangpan011/article/details/79461846

https://www.zhihu.com/question/21868680/answer/136376374

https://www.zhihu.com/question/21868680/answer/25599956

一、向量范数

①  1 范数：

，即向量元素绝对值之和，matlab  调用函数  norm(x, 1) 。

②  2 范数：（经常用到）

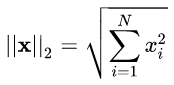，Euclidean norm（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab  调用函数  norm(x, 2)。

③  范数：

，即所有向量元素绝对值中的最大值，matlab  调用函数  norm ( x , inf ) 。

④  - 范数：

 ，即所有向量元素绝对值中的最小值，matlab  调用函数  norm ( x ,  - inf ) 。

⑤ P  范数：

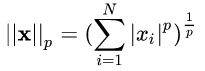，即向量元素绝对值的 p 次方和的  1/p 次幂，matlab  调用函数  norm ( x ,  p ) 。

二、矩阵范数

 ①  1  范数：

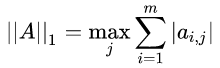，列和范数，即所有矩阵列向量绝对值之和的最大值，matlab  调用函数  norm ( A , 1 ) 。

②  2  范数：

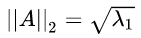，  λ₁ 为  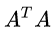的最大特征值。也叫谱范数，即所有矩阵行向量绝对值之和的最大值，matlab  调用函数 norm ( A ,  inf ) 。

③  F  范数：

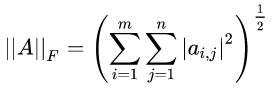，即矩阵元素绝对值的平方和再开平方，matlab  调用函数 norm ( A ,  ’fro‘ ) 。

④  核  范数：

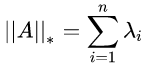， _{λi  是A的奇异值。即奇异值之和。}

 三、理解范数

0 范数：向量中非零元素的个数。

1 范数：为绝对值之和。

2 范数：就是通常意义上的模。

无穷范数：就是取向量的最大值。

要更好的理解范数，就要从函数、几何与矩阵的角度去理解：
       我们都知道，函数与几何图形往往是有对应的关系，这个很好想象，特别是在三维以下的空间内，函数是几何图像的数学概括，而几何图像是函数的高度形象化，比如一个函数对应几何空间上若干点组成的图形。但当函数与几何超出三维空间时，就难以获得较好的想象，于是就有了映射的概念，映射表达的就是一个集合通过某种关系转为另外一个集合。通常数学书是先说映射，然后再讨论函数，这是因为函数是映射的一个特例。
       为了更好的在数学上表达这种映射关系（这里特指线性关系）于是就引进了矩阵。这里的矩阵就是表征上述空间映射的线性关系。而通过向量来表示上述映射中所说的这个集合，而我们通常所说的基，就是这个集合的最一般关系。于是，我们可以这样理解，一个集合（向量），通过一种映射关系（矩阵），得到另外一个几何（另外一个向量）。那么向量的范数，就是表示这个原有集合的大小。而矩阵的范数，就是表示这个变化过程的大小的一个度量。那么说到具体几几范数，其不过是定义不同，一个矩阵范数往往由一个向量范数引出，我们称之为算子范数，其物理意义都如上述所述。

四、计算机领域对范数的理解

        具体怎么用，看不同的领域，计算机领域用的比较多的就是迭代过程中收敛性质的判断。在计算机领域，一般迭代前后步骤的差值的范数表示其大小，常用的是二范数，差值越小表示越逼近实际值，可以认为达到要求的精度，收敛。

       总的来说，范数的本质是距离，存在的意义是为了实现比较。比如，在一维实数集合中，我们随便取两个点  4  和  9 ，我们知道  9  比  4  大，但是到了二维实数空间中，取两个点（1，1）和（0，3），这个时候我们就没办法比较它们之间的大小，因为它们不是可以比较的实数，于是我们引入范数这个概念，把我们的（1，1）和（0，3）通过范数分别映射到实数   和  3 ，这样我们就可以比较这两个点了。所以你可以看到，范数它其实是一个函数，它把不能比较的向量转换成可以比较的实数。在上面的例子里，我们用的范数是平方求和然后再开方，范数还有很多其他的类型，这个就要看具体的定义了，理论上我们也可以把范数定义为只比较  x  轴上数字的绝对值。

五、在数学角度理解

引用邹教授上课时候的一段话来说明。

“佟湘玉有一天在同福客栈说：“额滴神呐，展堂，你说隔壁的赛貂蝉有什么好。”老白：“她没你温柔，没你贤惠，没你大气，没你端庄。”佟湘玉：“那为啥你们总往她那跑呢?”老白：“因为他的相貌是满分啊”。”

看到没有？如果用二范数来衡量 赛貂蝉 和 佟湘玉，那么可以说 佟湘玉 并不占下风，但是压不住人家 赛貂蝉 有一个满分啊，也就是说，从无穷范数的角度来看，赛貂蝉 稳稳的超过 佟湘玉 。

再看一个辩题“当今社会更需要通才还是专才”。通才是一范数二范数比较大，而专才就是无穷范数比较大。

发现了么？对于标量，我们可以通过加法直接比较大小，比如我一米七八就是比一米五高。那我问你，我身高体重是 [178,73] ，另一个人是 [176,66] ，你告诉我，谁更“优秀”？没办法做差了吧，那你还得想一种比较方式，这种比较方式就可以使用范数，而范数的特性决定了，它可以作为一种比较方式。

最后，记住，范数是比较向量/矩阵是否“优秀”的一种标准而已。