python神经网络理论

神经网络

• 其中每层的圆圈代表一个神经元，隐藏层和输出层的神经元有输入的数据计算后输出，输入层的神经元只是输入
• 神经网络的特点：

每个连接都有个权值

同一层神经元之间没有连接

最后的输出结果对应的层也称之为全连接层

感知肌

• 感知肌是一种最基础的分类模型，类似逻辑回归，感知肌用的激活函数sign，而逻辑回归用的sigmoid，感知肌也具有连接的权重和偏置
• 感知肌可以解决的问题：

或

与

• 通常一个感知肌不能解决很多问题，需要多添加几个感知肌，还有激活函数
• ​​http://playground.tensorflow.org/#activation=linear&batchSize=10&dataset=gauss&regDataset=reg-plane&learningRate=0.03&regularizationRate=0&noise=0&networkShape=1&seed=0.06097&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false​​

神经网络原理

• softmax回归：logits（线性回归的输出）+softmax映射 →解决多分类问题

• 损失函数,提高真实值1所在的预测概率
  交叉熵损失
  总损失 - 平均值
• 

最小二乘法 - 线性回归的损失 - 均方误差

• 优化损失函数

卷神经

• 发展历史

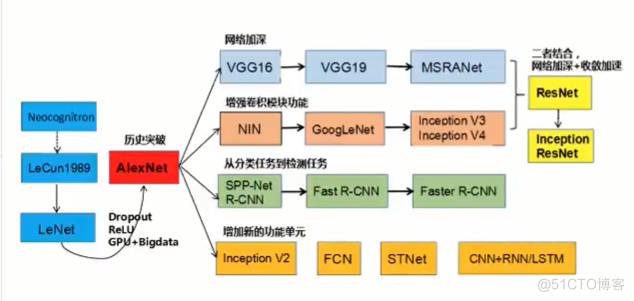
• 卷神经网络-结构
  卷积层
  激活层
  池化层
  全连接层
• 卷积神经网络和传统神经网络相比
  输入层
  隐藏层
  卷积层：通过在原始图像上平移来提取特征
  激活函数：增加非线性分割能力
  池化层：减少学习参数，减低网络复杂度【增大池化和平均池化】
  全连接层
  输出层
• 卷积层

• 个数
• 大小 11 23 5*5
  如何计算？
  输入
  55=1 filter 33*1 步长 1
  输出
  3*3 = 1
• 步长
  输入
  55 filter 33 *1步长 2
  输出
  221
• filter观察
• 
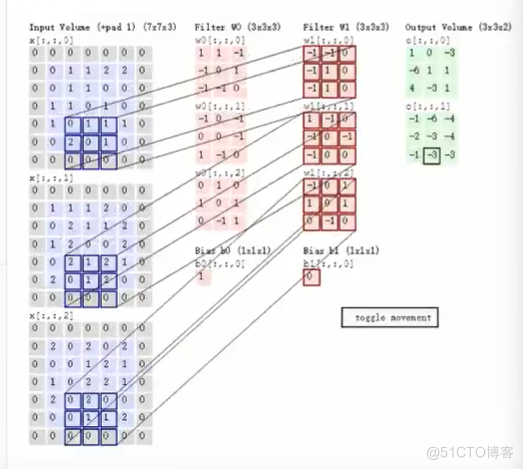
• 输出计算公式

• 

• 卷积API
• 

• 池化层
• 
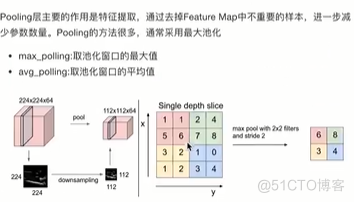
• 池化层API
• 
• 全连接层

• 在隐藏层和全连接层之间，起到作用是分类的作用

• 计算练习