集成学习:Bagging Boosting&Stacking
- 1.简介
- 2.Bagging
- 2.1 Bootstrapping
- 3.Boosting
- 4.Stacking
- 何时使用集成学习?
1.简介
在我看来集成学习很像是每年的艺考,每一轮考试面试,需要面对不同的专业的老师,这些老师,从不同专业(形体,声乐,舞蹈)等角度对学生进行打分,如果满分是100,还要按照不同比例(形态30%,声乐30%,舞蹈40%)结合给出学生的综合得分。根据这个得分来作为录取学生的标准。

机器学习中的集成建模基于相同的原理,我们将多个模型的预测结合起来,生成最终的模型,从而提供更好的整体性能。集成建模有助于推广基于训练数据的学习,从而能够对未知数据进行准确预测。
建模是机器学习过程中最重要的一步。集成学习背后的主要动机是正确地组合弱模型,以获得更准确、更稳健的模型,并进行偏差-方差权衡。例如,随机森林算法是决策树的集成,由于它结合了多个决策树模型,所以它的性能总是优于单个决策树模型。
根据我们如何组合基本模型,集成学习可以分为三种不同类型:
- Bagging
- Boosting
- Stacking
2.Bagging
回归任务
Bagging模型如下,Boostrap Sample是抽样的方法,最后预测的结合,可以用不同的聚合算法,如mean。
分类任务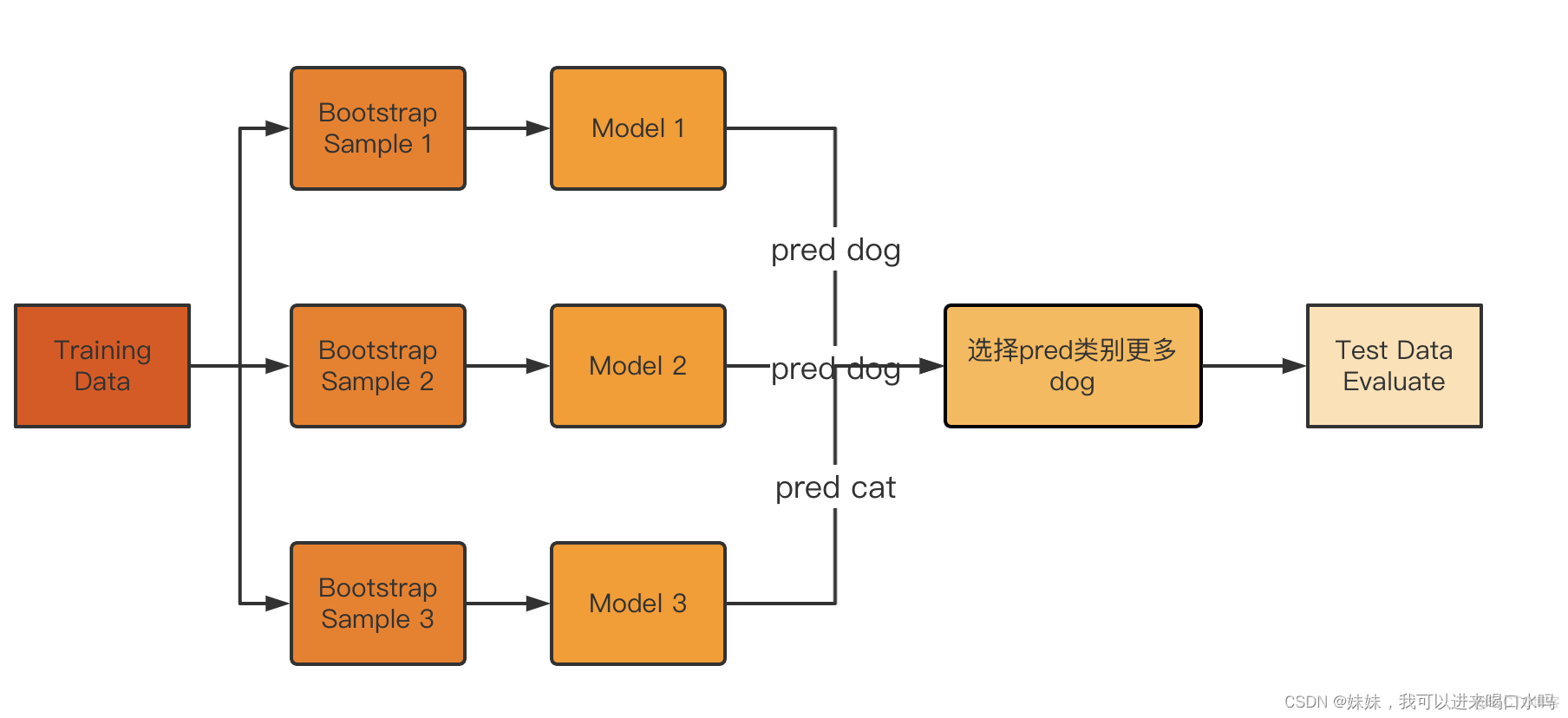
- 在bagging中,我们对原始数据集采用抽样的方法来建立独立的估计量,并对所有预测进行平均或投票。
- 由于多个模型预测的平均值一起形成最终预测,bagging减少了方差,有助于避免过度拟合。虽然它通常用于决策树方法,但它可以用于任何类型的方法。
- Bagging是模型平均法的一个特例,在回归问题中,我们取输出的平均值,在分类中,我们取多数票,就是所有模型预测这个类别的数量占多数,就把这个数据预测为这个类。
- 如果我们有过拟合(高方差)的基础模型,bagging会更有帮助
- 最流行的套袋估计器是“bagging树”,也称为“随机森林”
2.1 Bootstrapping
Bootstrapping方法的实现很简单,假设抽取的样本大小为n:
在原样本中有放回的抽样,抽取n次。每抽一次形成一个新的样本,重复操作,形成很多新样本,通过这些样本就可以计算出样本的一个分布。新样本的数量通常是1000-10000。如果计算成本很小,或者对精度要求比较高,就增加新样本的数量。
优点:简单易于操作。
缺点:bootstrapping的运用基于很多统计学假设,因此假设的成立与否会影响采样的准确性
3.Boosting
- 在boosting的情况下,机器学习模型被一个接一个地使用,第一层模型的预测被用作下一层模型的输入。最后一层模型将使用之前所有层的预测来获得最终预测。
- 因此,boosting使每个后续模型都能够通过克服或减少前一个模型的错误来提高前一个模型的性能。
- 与bagging不同的是,在提高基础的情况下,学习者按照加权版本的数据顺序进行训练。如果我们有偏见的基本模型,那么推进会更有帮助。
- Boosting可以用来解决回归和分类问题

不同类型的Boosting算法:
- 梯度增压机(GBM)
- 极端梯度增压机(XGBM)
- LightGBM
- CatBoost
4.Stacking
模型Stacking(叠加)是一种组合模型以减少其偏差的方法。每个单独模型的预测叠加在一起,并作为最终估计器的输入来计算预测。通过交叉验证对最终估计器进行训练。
注意,在堆叠的情况下,我们使用异构弱学习者(不同的学习算法),但在bagging和boosting的情况下,我们主要使用同质弱学习者(同一学习算法)。
stacking是一种分层模型集成框架。以两层为例,第一层由多个基学习器组成,其输入为原始训练集,第二层的模型则是以第一层基学习器的输出作为特征加入新模型进行再训练(通常是为了防止过拟合会采用简单的模型),从而得到完整的stacking模型
这里举例:第一层模型分别用XGB,GBDT,第二层用LR线性回归,我们的数据集有1250个,现在分层1000训练集和250测试集,我们用k折法对训练集进行划分,划分成5份。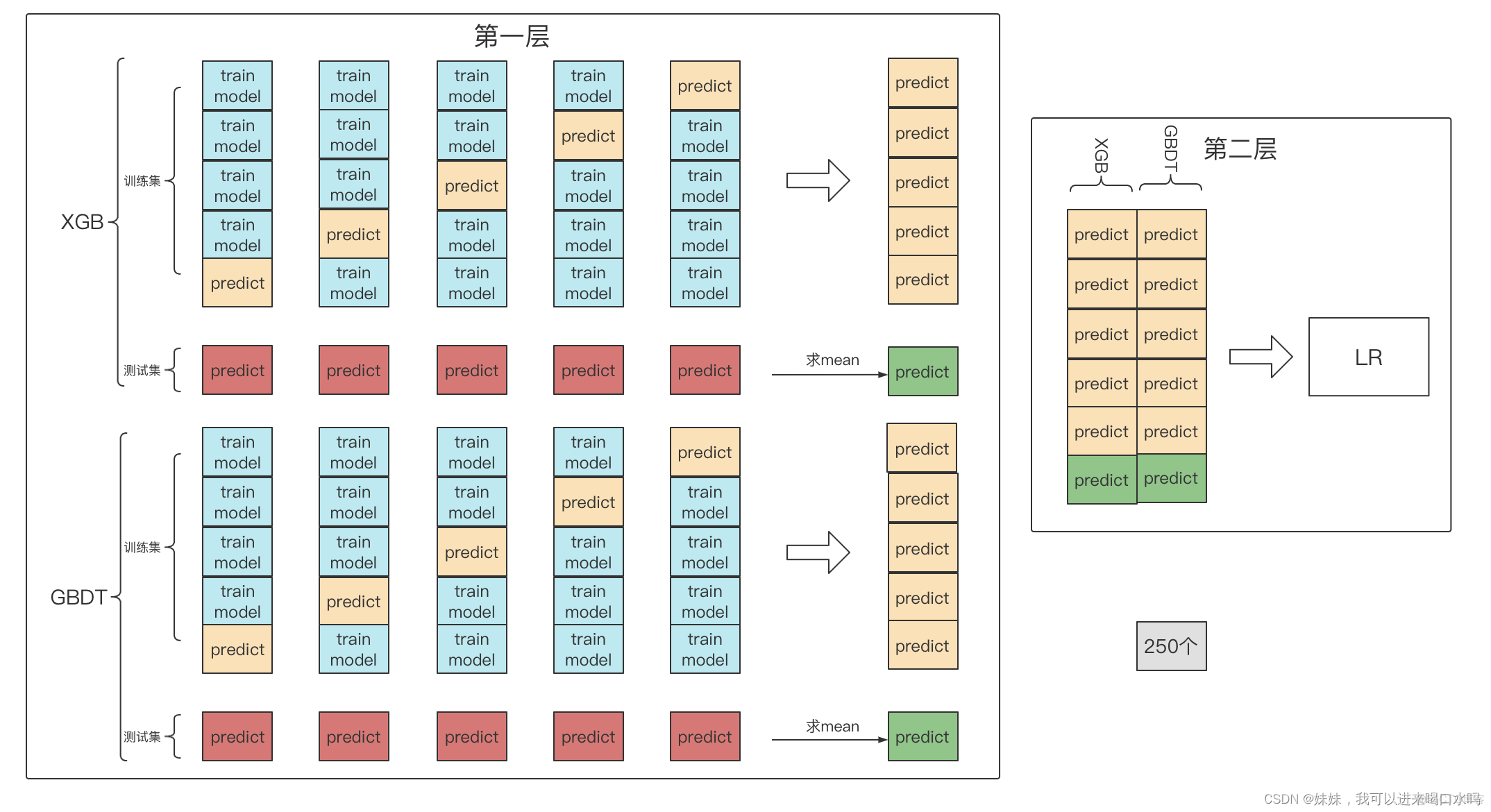
蓝色的数据集,被拿去训练模型了,黄色的数据集,拿去验证数据集,生成它的预测值。红色的测试集拿去模型去预测
何时使用集成学习?
既然集成学习能带来更好的准确性、高一致性,也有助于避免偏差-方差权衡,那么我们不应该在任何地方都使用它吗?
简而言之,这取决于手头的问题。如果我们拥有可用训练数据的模型表现不佳,并且显示出过度拟合/不拟合的迹象,并且额外的计算能力不是问题,那么进行集成学习是最佳选择。然而,在使用简单方法之前,不应该跳过改进输入数据和尝试不同超参数的第一步。
