计算机视觉PyTorch实现（一）

计算机视觉PyTorch实现（一）

PyTorch基础模块

计算机视觉可以被广泛应用于多个现实领域中。如做图像基本处理、图像识别、图像分割、目标跟踪、图像分类、姿态估计等。在深度学习中人们开发了很多的学习框架，如Caffe、MXNet、Pytorch和TensorFlow等。这些框架可以极大简化了构建深度学习神经网络的过程。
在计算机视觉应用中通过pytorch模块构建不同的神经网络在不同网络层提取不同的类型特征，来实现不同的应用功能。
这里先对pytorch基础的几个模块展开学习。

这里先导入对应用到的基础包

import torch.nn as nn
import torch

1.线性层

线性层也叫全连接层，该层一般出现在网络的最后一层中
定义代码如下：

nn.Linear(in_features,out_features,bias=True)

• in_features：代表输入的特征维度
• out_features：代表输出的特征维度
• bias：是否引入偏置参数
  这层实际上执行了一个最简单的线性回归模型，相当于做了一个矩阵乘法和矩阵加法 y=x*W+b

2.卷积层

在深度学习模型中，最核心的部分就是卷积层。对于图像来说，卷积运算是一种图像线性变换，在卷积操作的运算涉及两个张量，第一个张量为输入张量，第二个张量是线性变换的权重张量也称为卷积核。

定义代码如下：

class _ConvNd(in_channels,out_channels,kernel_size,stride,padding,dilation,transposed,output_padding,groups,bias,padding_mode)

• in_channels：输入通道数，举例：一张彩色的图像，就是由R、G、B三种通道构成。
• out_channels :输出通道，及卷积核的通道数
• kernel_size:；这个值代表卷积核的维度大小，对于二维卷积来说，这个值可以是一个元组。举例（3，4），意味着卷积核的大小是3x4。
• stride：在卷积核中卷积运算的步长
• padding：填充输入的张量空间大小
  
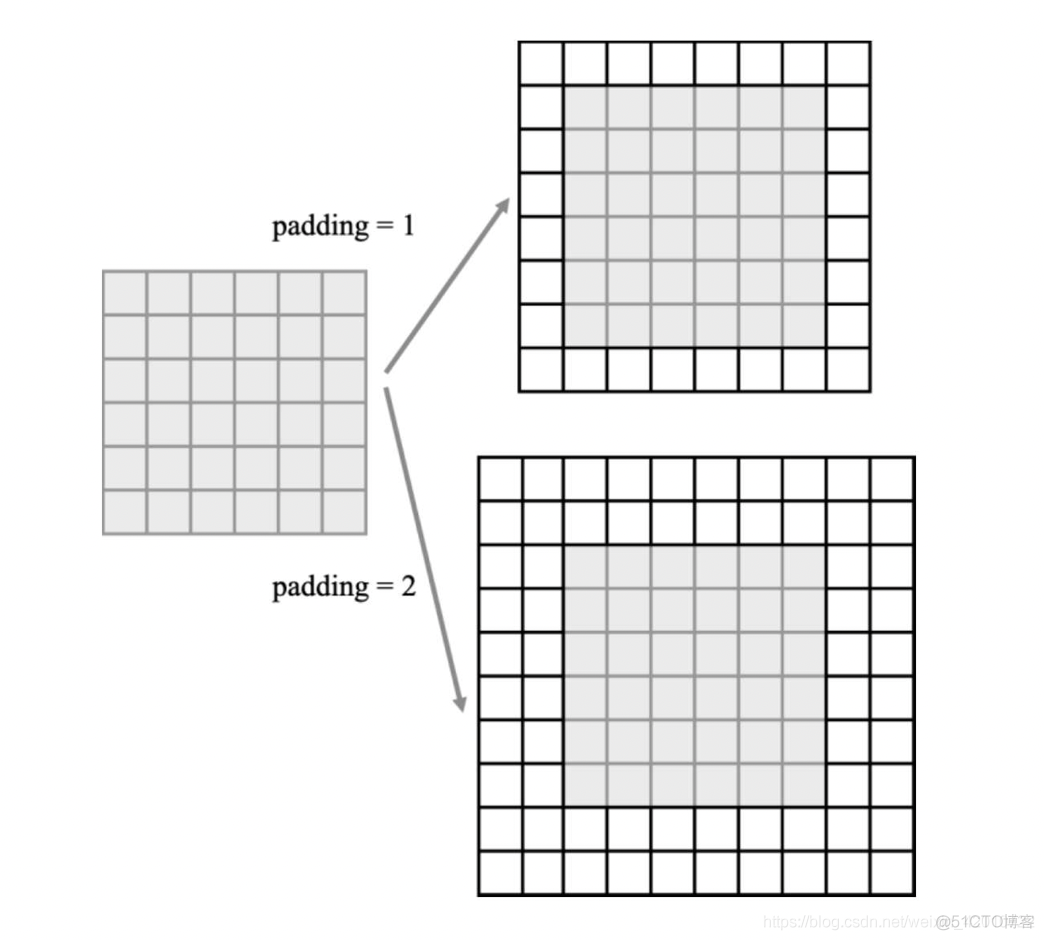
• dilation：另一种扩张卷积方法
• transposed：转置卷积，如果为False进行普通卷积的计算，如果为True进行转置卷积计算

3.归一化层

归一化层，有很多种，包括：

• 批次归一化

nn.BatchNorm2d(num_features,eps=1e-05,momentum=0.1,affine=True,track_running_stats=True)

• 组归一化
• 实例归一化
• 层归一化
• 局部响应归一化
  几乎所有的归一化都类似于如下表达方式，其中x是输入的张量的值，和是可以训练的向量参数，其元素的数目和输入张量的通道数目相等，它们区别在于归一化的平均值的计算方式和归一化的方差的计算方式不同。
  

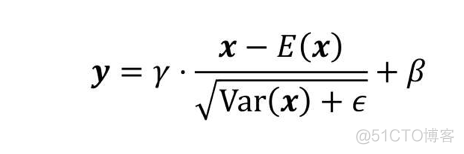
4.池化层

最大池化层：选定某一卷积核区域，取这个区域中输入张量最大值，根据输入张量形状不同，最大池化层可以分为一维、二维和三维。
代码如下：

nn.MaxPool2d(kernel_size,stride=None,padding=0,dilation=1,return_indice=False,ceil_mode=False)

• kernel_siz：这里的卷积核不做计算处理，而是在输入张量的卷积核内选择最大的值。
• return_inices：决定是否返回最大元素所在位置。
• ceil—mode：最大层池化层最后输出是否向上取整。

5.dropout层

我们都知道，神经网络的复杂性和神经元的连接方式有关，神经元连接越多，模型越复杂。月容易发生过拟合，为了减少神经网络过拟合，通过减少神经元连接来进一步实现使模型泛化。
减少神经网络的连接实现相对比较复杂，一个等价最简单的方式是把激活函数张量和权重张量的元素随机置为零。

nn.Dropout2d(p=0.5,inplace=False)

6.模块组合

下面通过使用nn.Sequential来构造顺序模块。

# 方法1.使用参数来构建顺序模型
model=nn.Sequential(
nn.Conv2d(1,20,5),
nn.ReLU(),
nn.Conv2d(20,64,5),
nn.ReLU())
# 方法2.使用顺序字典来构建模型
model=nn.Sequential(OrdereDict([
('conv1',nn.Conv2d(1,20,5)),
('relu1',nn.ReLU()),
('conv2',nn.Conv2d(20,64,5)),
('relu2',nn.ReLU())]))

7.特征提取

在计算机视觉应用中。通过深度学习模型中间层计算产生一系列从简单到复杂的特征，并最后提取得到复杂特征来进行预测的，也就是说深度学习神经网络模型分为二部分：第一部分，对原数据集进行特征提取，第二部分，对提取到的特征进行重新组合产生预测概率值。
在计算机视觉应用中，为了实现相应的应用，如图像分类。大佬们研究出许多的深度学习模型，即通过不同的卷积层，池化层等模块组合，构造出不同的神经网络模型。如图像分类模型算法。

这里通过构建一个AlexNet实例让大家更快的了解pytorch构建神经网络模型的方法及其对应模版。

class AlexNet(nn.Module):
#定义分类种类 10
def __init__(self, num_classes=10):
super(AlexNet, self).__init__()
#特征提取
self.features = nn.Sequential(
nn.Conv2d(3, 48, kernel_size=11, stride=4, padding=2), # input[3, 224, 224] output[48, 55, 55]
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2), # output[48, 27, 27]
nn.Conv2d(48, 128, kernel_size=5, padding=2), # output[128, 27, 27]
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2), # output[128, 13, 13]
nn.Conv2d(128, 192, kernel_size=3, padding=1), # output[192, 13, 13]
nn.ReLU(inplace=True),
nn.Conv2d(192, 192, kernel_size=3, padding=1), # output[192, 13, 13]
nn.ReLU(inplace=True),
nn.Conv2d(192, 128, kernel_size=3, padding=1), # output[128, 13, 13]
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2), # output[128, 6, 6]
)
#特征组合分类
self.classifier = nn.Sequential(
nn.Dropout(p=0.5),
nn.Linear(128 * 6 * 6, 2048),
nn.ReLU(inplace=True),
nn.Dropout(p=0.5),
nn.Linear(2048, 2048),
nn.ReLU(inplace=True),
nn.Linear(2048, num_classes),
)

def forward(self, x):
x = self.features(x)
x = torch.flatten(x, start_dim=1)
x = self.classifier(x)
return x