【偷偷卷死小伙伴Pytorch20天】-【day6】-【自动微分机制】

系统教程20天拿下Pytorch​ 最近和中哥、会哥进行一个小打卡活动，20天pytorch，这是第6天。欢迎一键三连。

文章目录

• ​​一、利用backward方法求导数​​

• ​​1, 标量的反向传播​​
• ​​2, 非标量的反向传播​​
• ​​3, 非标量的反向传播可以用标量的反向传播实现​​

• ​​二、利用autograd.grad函数求导数​​
• ​​三、利用自动微分和优化器求最小值​​
• ​​总结​​

神经网络通常依赖反向传播求梯度来更新网络参数，求梯度过程通常是一件非常复杂而容易出错的事情。

而深度学习框架可以帮助我们自动地完成这种求梯度运算。

Pytorch一般通过反向传播 backward 方法 实现这种求梯度计算。该方法求得的梯度将存在对应自变量张量的grad属性下。

除此之外，也能够调用torch.autograd.grad 函数来实现求梯度计算。

这就是Pytorch的自动微分机制。

一、利用backward方法求导数

backward 方法通常在一个标量张量上调用，该方法求得的梯度将存在对应自变量张量的grad属性下。

如果调用的张量非标量，则要传入一个和它同形状 的gradient参数张量。

相当于用该gradient参数张量与调用张量作向量点乘，得到的标量结果再反向传播。

1, 标量的反向传播

import numpy as np
import torch

# f(x) = a*x**2 + b*x + c的导数

x = torch.tensor(0.0,requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c

y.backward()
dy_dx = x.grad
print(dy_dx)

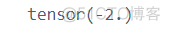
requires_grad = True可以将其理解为开启自变量

2, 非标量的反向传播

import numpy as np
import torch

# f(x) = a*x**2 + b*x + c

x = torch.tensor([[0.0,0.0],[1.0,2.0]],requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c

gradient = torch.tensor([[1.0,1.0],[1.0,1.0]])

print("x:\n",x)
print("y:\n",y)
y.backward(gradient = gradient)
x_grad = x.grad
print("x_grad:\n",x_grad)

对于非标量来说，是求点积，到最后出来一个标量才能求导

3, 非标量的反向传播可以用标量的反向传播实现

这里也就是解释了 2, 非标量的反向传播

import numpy as np
import torch

# f(x) = a*x**2 + b*x + c

x = torch.tensor([[0.0,0.0],[1.0,2.0]],requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c

gradient = torch.tensor([[1.0,1.0],[1.0,1.0]])
z = torch.sum(y*gradient)
# y.backward(gradient=gradient)

print("x:",x)
print("y:",y)
z.backward()
x_grad = x.grad
print("x_grad:\n",x_grad)

二、利用autograd.grad函数求导数

import numpy as np
import torch

# f(x) = a*x**2 + b*x + c的导数

x = torch.tensor(0.0,requires_grad = True) # x需要被求导
a = torch.tensor(1.0,requires_grad = True)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)
y = a*torch.pow(x,2) + b*x + c


# create_graph 设置为 True 将允许创建更高阶的导数
dy_dx = torch.autograd.grad(y,x,create_graph=True) # 返回数组
print(dy_dx)

# 求二阶导数
dy2_dx2 = torch.autograd.grad(dy_dx,x)[0]

print(dy2_dx2.data)

import numpy as np
import torch

x1 = torch.tensor(1.0,requires_grad = True) # x需要被求导
x2 = torch.tensor(2.0,requires_grad = True)

y1 = x1*x2
y2 = x1+x2


# 允许同时对多个自变量求导数
(dy1_dx1,dy1_dx2) = torch.autograd.grad(outputs=y1,inputs = [x1,x2],retain_graph = True)
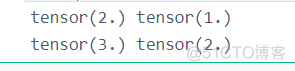
print(dy1_dx1,dy1_dx2)

# 如果有多个因变量，相当于把多个因变量的梯度结果求和
(dy12_dx1,dy12_dx2) = torch.autograd.grad(outputs=[y1,y2],inputs = [x1,x2])
print(dy12_dx1,dy12_dx2)

三、利用自动微分和优化器求最小值

import numpy as np
import torch

# f(x) = a*x**2 + b*x + c的最小值

x = torch.tensor(0.0,requires_grad = True) # x需要被求导
a = torch.tensor(1.0)
b = torch.tensor(-2.0)
c = torch.tensor(1.0)

optimizer = torch.optim.SGD(params=[x],lr = 0.01)


def f(x):
result = a*torch.pow(x,2) + b*x + c
return(result)

for i in range(500):
optimizer.zero_grad()
y = f(x)
y.backward()
optimizer.step()


print("y=",f(x).data,";","x=",x.data)

总结

标量求导和非标量求导及其本质（requires_grad=True）
autograd.grad函数求导数
torch.autograd.grad(y,x,create_graph=True) # 返回数组
(dy12_dx1,dy12_dx2) = torch.autograd.grad(outputs=[y1,y2],inputs = [x1,x2])如果有多个因变量，相当于对梯度求和
梯度下降算法求最小值（梯度清0，求梯度，梯度更新）