【python基础】第19回 多层，有参装饰器 递归 二分法

本章内容概要

1. 多层装饰器

2. 有参装饰器

3. 递归函数

4. 算法（二分法）

本章内容详解 1. 多层装饰器 1.1 什么是多层装饰器

多层装饰器是从下往上依次执行，需要注意的是，被装饰的函数名所指代的函数是一直被装饰器中的内层函数所取代。

1.2 语法糖的功能

会自动将下面紧挨着的函数名当做参数传递给@符号2后面的函数名（加括号调用）

1.3 代码讲解

def outter1(func1):  # 13.func1 = wrapper2函数名
    print('加载了outter1')  # 14.第三个打印
    def wrapper1(*args, **kwargs):
        print('执行了wrapper1')
        res1 = func1(*args, **kwargs)
        return res1
    return wrapper1  # 15.返回wrapper1

def outter2(func2):  # 9.func2 = wrapper3函数名
    print('加载了outter2') # 10.第二个打印
    def wrapper2(*args, **kwargs):
        print('执行了wrapper2')
        res2 = func2(*args, **kwargs)
        return res2
    return wrapper2  # 11.返回wrapper2

def outter3(func3):  # 4.func3 = 真正的index函数
    print('加载了outter3')  # 5.第一个打印
    def wrapper3(*args, **kwargs):
        print('执行了wrapper3')
        res3 = func3(*args, **kwargs)
        return res3
    return wrapper3  # 6.返回wrapper3


@outter1  # 12.index = outter1(wrapper2)  调用outter1 把 outter2参数传进去 上面没有语法糖 最后用被装饰的函数一样的名字接受函数
@outter2  # 8.wrapper2 = outter2(wrapper3) 调用outter2 把 outter3参数传进去
@outter3  # 7.wrapper3 = outter3(真正的index函数名)  传给@outter2
# 1.如果上面没有其他语法糖了同名的函数名赋值一下index = = outter3(把真正的index函数名传进去)，
# 2.如果语法糖叠加在一起的话，只有到最后一步才会使用和真正装饰的和函数名一样的名字去赋值，如果不到最后一步)
# 3.函数名加括号执行优先级最高 先执行outter3
def index():
    print('from index')
index()
# 多层语法糖解读顺序是先看语法糖有几个，然后再由下往上去看，遇到最后一个才会使用相同的变量名传给装饰器函数使用
# 语法糖三：wrapper3 = outter3(index),加载了outter3
# 语法糖二：wrapper2 = outter2(wrapper3)，加载了outter2
# 语法糖一；index = outter1(wrapper2),加载了outter1
# 执行顺序就是：wrapper1>>>>>wrapper2>>>>>wrapper3
# 加载outer3>>>加载outer2>>>加载outer1>>>index()>>>运行wrapper1函数体代码>>>然后再执行outer2函数体代码>>>然后再执行wrapper3的函数体代码

2. 有参装饰器 2.1 什么是有参装饰器

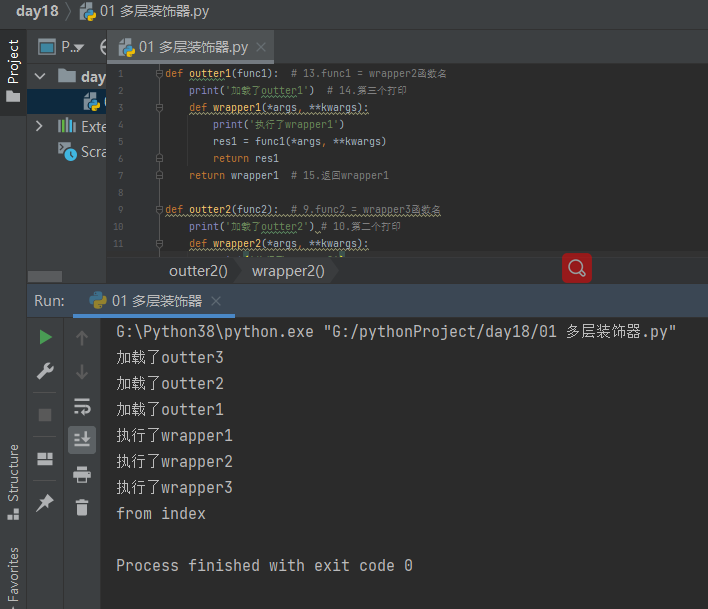
是为装饰器提供多样功能选择的实现提供的，实现原理是三层闭包

2.2 代码讲解

初始代码

def login_auth(func_name):
    def inner(*args, **kwargs):
        username = input('username>>>:').strip()
        password = input('password>>>:').strip()
        if username == 'jason' and password == '123':
            res = func_name(*args, **kwargs)
            return res
        else:
            print('用户权限不够 无法调用函数')
    return inner

实现：在装饰器内部可以切换多种数据来源 ，如 列表 ，字典 ，文档

def outer(condition,type_user):
    def login_auth(func_name):  # 这里不能再填写其他形参
        def inner(*args, **kwargs):  # 这里不能再填写非被装饰对象所需的参数
            username = input('username>>>:').strip()
            password = input('password>>>:').strip()
            # 应该根据用户的需求执行不同的代码
            if type_user =='jason':print('VIP')
            if condition == '列表':
                print('使用列表作为数据来源 比对用户数据')
            elif condition == '字典':
                print('使用字典作为数据来源 比对用户数据')
            elif condition == '文件':
                print('使用文件作为数据来源 比对用户数据')
            else:
                print('去你妹的 我目前只有上面几种方式')
        return inner
    return login_auth
@outer('列表','jason')
def index():
    print('from index')
index()

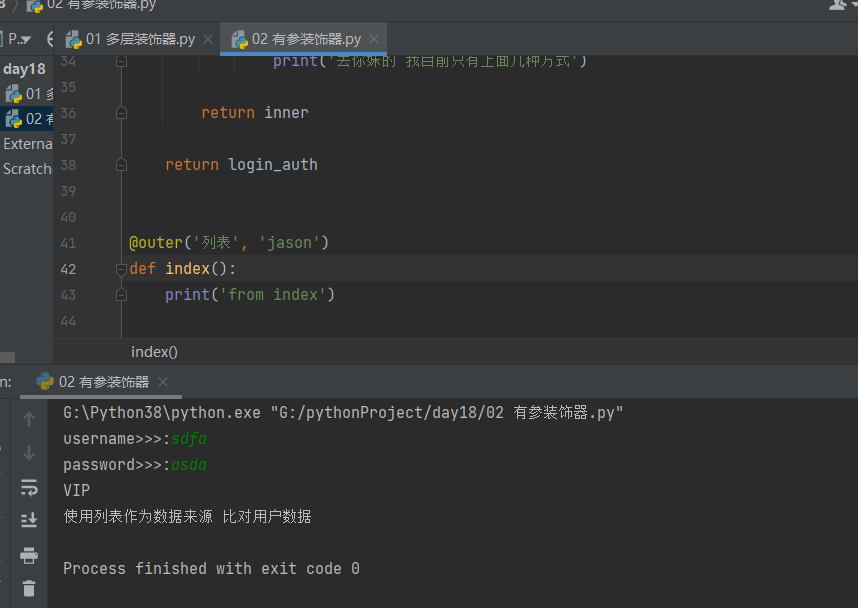3. 递归函数 3.1 什么是递归函数

编程语言中，函数直接或间接调用函数本身，则该函数称为递归函数。

3.2 代码讲解 递归调用：直接调用

def index():
    print('from index')
    index()

index()

有返回值

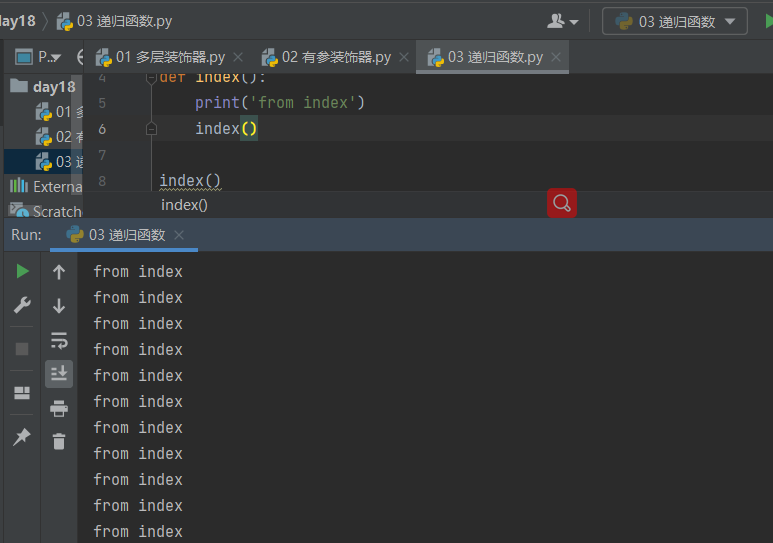
也会报错，调用Python对象时超过最大递归深度

3.3 代码讲解 递归调用：间接调用

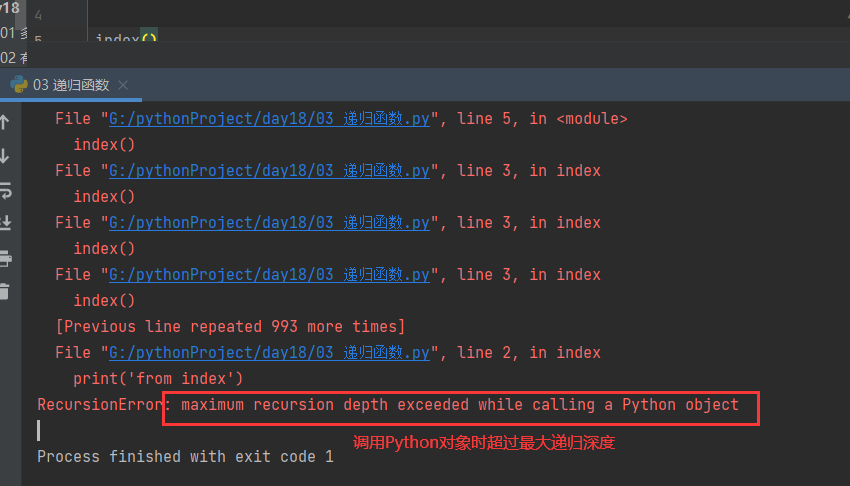
# 递归调用:间接调用
def index():
    print('from index')
    func()

def func():
    print('from func')
    index()

func()

有返回值

 也会报错，调用Python对象时超过最大递归深度

 3.4 python 中允许函数最大递归调用的次数

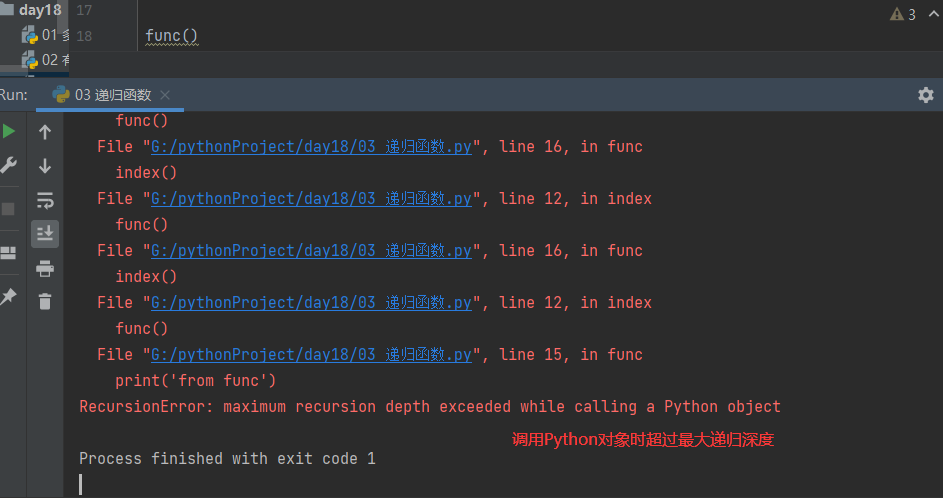
1. 官方给出的限制是1000 用代码去验证可能会有些许偏差(997 998...)

count = 0  # count = 1
def index():
    print('from index')
    global count
    count += 1  # count = count + 1
    print(count)
    index()
index()

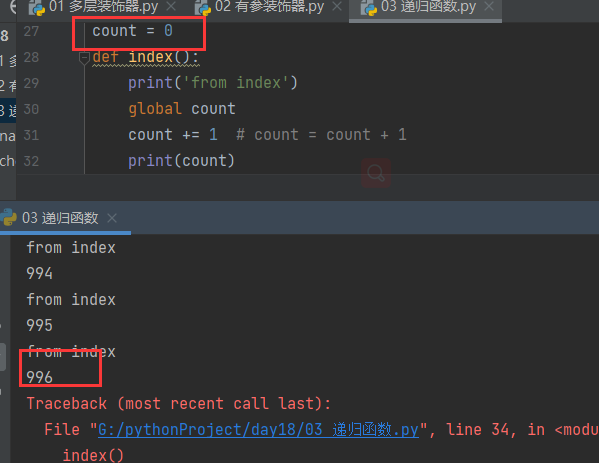
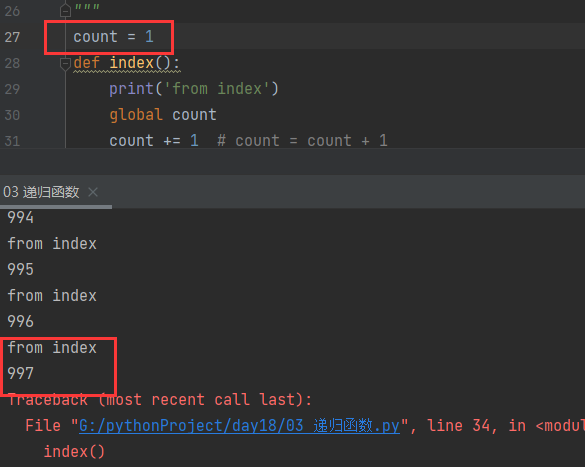
2. python 解释器获取递归最大次数

import sys
print(sys.getrecursionlimit())  # 1000  获取递归最大次数

3. 自定义递归递归最大次数

import sys
sys.setrecursionlimit(1500)  # 自定义最大次数
print(sys.getrecursionlimit())

 3.4 递归函数真正的应用场景

1. 递归函数真正的应用场景

    递推:一层层往下寻找答案

    回溯:根据已知条件推导最终结果

2. 递归函数
   1.每次调用的时候都必须要比上一次简单!
   2.并且递归函数最终都必须要有一个明确的结束条件!

3. 讲解  **空列表自动结束

l1 = [1, [2, [3, [4, [5, [6, [7, [8, [9, [10, ]]]]]]]]]]
# 循环打印出列表中所有的数字
# 1.for循环l1里面所有的数据值
# 2.判断当前数据值是否是数字 如果是则打印
# 3.如果不是则继续for循环里面所有数据值
# 4.判断当前数据值是否是数字 如果是则打印
# 5.如果不是则继续for循环里面所有数据值
# 6.判断当前数据值是否是数字 如果是则打印

def get_num(l1):
    for i in l1:
        if isinstance(i,int):
            print(i)
        else:
            get_num(i)
get_num(l1)

4. 算法（二分法） 4.1 什么是算法  算法就是解决问题的方法

       算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间，空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

       二分法 快拍 插入 堆排 链表 双向链表 约瑟夫问题

4.2 什么是二分法

       二分法是所有算法里面最简单的算法，是一种非常高效的算法,它常常用于计算机的查找过程中

4.3 二分法场景应用代码讲解

 在列表l1中，找到999，该列表无限长，简洁的取少部分

l1 = [11, 23, 32, 45, 65, 78, 90, 123, 432, 467, 567, 687, 765, 876, 999, 1131, 1232]


def get_num(l1, target_num):
    # 添加递归函数的结束条件
    if len(l1) == 0:
        print('不好意思 找不到')
        return
    # 1.先获取数据集中间那个数
    middle_index = len(l1) // 2
    middle_value = l1[middle_index]
    # 2.判断中间的数据值与目标数据值孰大孰小
    if target_num > middle_value:
        # 3.说明要查找的数在数据集右半边  如何截取右半边
        right_l1 = l1[middle_index + 1:]
        # 3.1.获取右半边中间那个数
        # 3.2.与目标数据值对比
        # 3.3.根据大小切割数据集
        # 经过分析得知 应该使用递归函数
        print(right_l1)
        get_num(right_l1, target_num)
    elif target_num < middle_value:
        # 4.说明要查找的数在数据集左半边  如何截取左半边
        left_l1 = l1[:middle_index]
        # 4.1.获取左半边中间那个数
        # 4.2.与目标数据值对比
        # 4.3.根据大小切割数据集
        # 经过分析得知 应该使用递归函数
        print(left_l1)
        get_num(left_l1, target_num)
    else:
        print('找到了', target_num)


get_num(l1, 999)

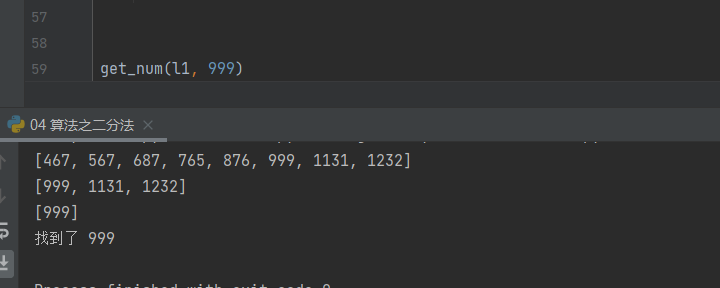4.4 二分法的缺陷

1. 数据集必须是有序的

2. 查找的数如果在开头或者结尾 那么二分法效率更低（for 循环）

作业 1.尝试编写有参函数将多种用户验证方式整合到其中

直接获取用户数据比对
数据来源于列表 数据来源于文件

2.尝试编写递归函数

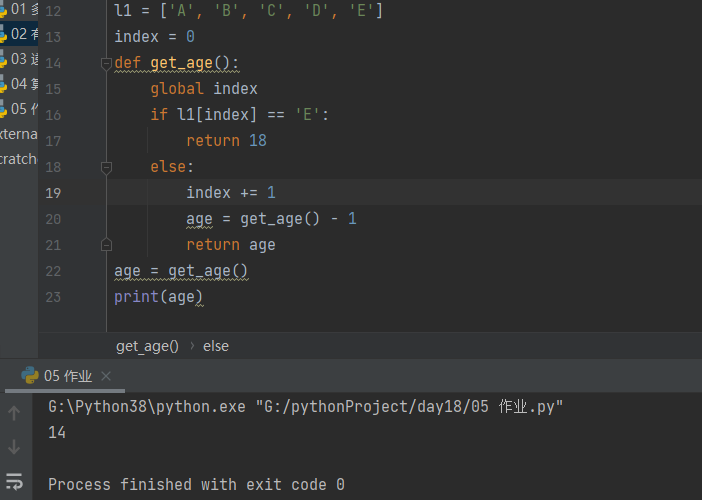
推导指定某个人的正确年龄
eg: A B C D E 已知E是18 求A是多少

l1 = ['A', 'B', 'C', 'D', 'E']
index = 0
def get_age():
    global index
    if l1[index] == 'E':
        return 18
    else:
        index += 1
        age = get_age() - 1
        return age
age = get_age()
print(age)

3.自行查阅资料 提前收集常见算法快排 插入 冒泡等 3.1 快排

快排 全名 快速排序算法
快速排序（QuickSort）是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1962年提出。

它的基本思想是：
1. 从要排序的数据中取一个数为“基准数”。
2. 通过一趟排序将要排序的数据分割成独立的两部分，其中左边的数据都比“基准数”小，右边的数据都比“基准数”大。
3. 然后再按步骤2对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
该思想可以概括为：挖坑填数 + 分治法。分治法（分而治之）

3.2 插入

插入算法是一种排序算法

在运用插入算法时一般将数据分为两组，有序组和无序组，并且将数据的第一个元素默认为有序组，将无序组的元素一个一个按照某种排列方式插入到有序组中。

3.3 冒泡

冒泡算法是一种经典的排序算法，冒泡，顾名思义就是轻（小）的往上冒，重（大）的往下沉，也称鸡尾酒算法

解析首先我们需要确立两层嵌套for循环，第一层for循环主要控制总体循环的趟数，第二层for循环主要是比对相邻的两个数，运用CAS（比较并替换）的思路将每一趟的第二层for循环执行完成

 

【本文来源：韩国服务器 http://www.558idc.com/kt.html欢迎留下您的宝贵建议】