并查集和其他树形结构不一样,是由孩子指向父亲,它解决了一些连接问题,怎么才能确定两个点是否相连呢?并查集可以非常快的确定两个点是否连接。 如何确定连个点是否连接呢?
并查集和其他树形结构不一样,是由孩子指向父亲,它解决了一些连接问题,怎么才能确定两个点是否相连呢?并查集可以非常快的确定两个点是否连接。


我们可以用一个数组表示,对于0到9每个不同的编号可以表示不同的对象,这里可以看作一个点,而编号对应的不同的元素可以表示不同的集合,其中[0,2,4,6,8]表示一个集合。这样就可以表示连接问题了,0和2就是表示相连接,因为它们在一个集合,0和1因不在一个集合所以不连接。
对于一组数据并查集主要支持两个动作:
- isConnected(p,q):查询元素p和q是否在一个集合
- unionElements(p,q):合并元素p和q的集合
#pragma once
class UF {
private:
virtual const int getSize() const noexcept = 0;
virtual bool isConnected(int p, int q) = 0;
virtual void unionElements(int p, int q) = 0;
};
#pragma once
#include "UF.h"
#include<cassert>
class UnionFind1 : public UF {
private:
int *id;
int size;
public:
UnionFind1(int capacity) {
id = new int[capacity];
size = capacity;
for (int i = 0; i < size; ++i) {
id[i] = i; //初始化不同的元素表示不同的集合都不相连
}
}
const int getSize() const noexcept {
return size;
}
//返回p所在的集合
int find(int p) {
assert(p >= 0 && p < size);
return id[p];
}
//判断是否相连
bool isConnected(int p, int q) {
return find(p) == find(q);
}
//合并集合
void unionElements(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) {
return;
}
for (int i = 0; i < size; ++i) {
if (id[i] == pID) {
id[i] = qID; //让两个集合都相同就行了
}
}
}
};
从代码中可以看到:
- unionElements的时间复杂度是O(n)
- isConnected的时间复杂度是O(1)
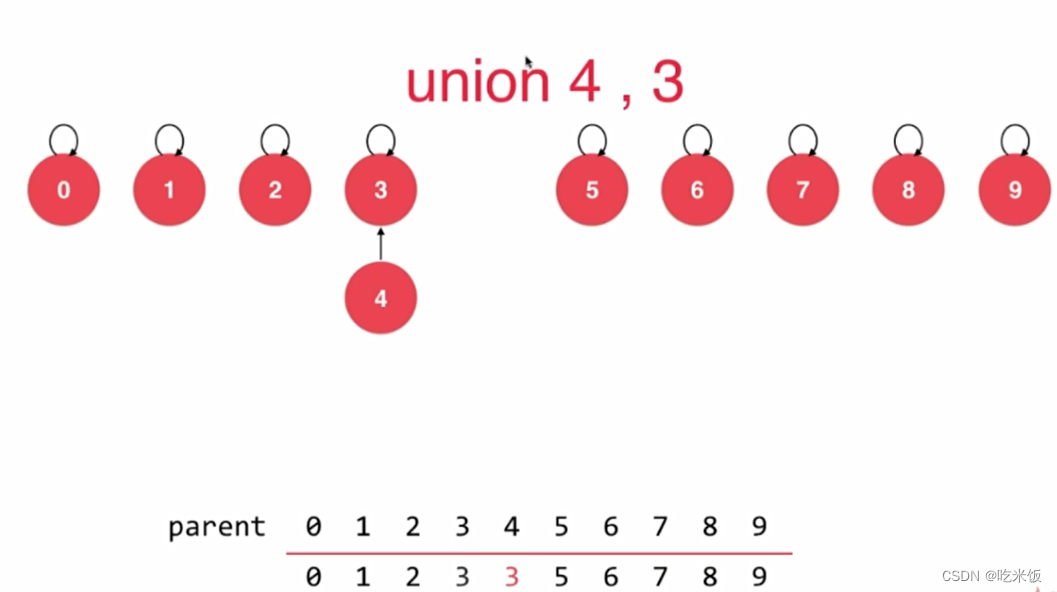
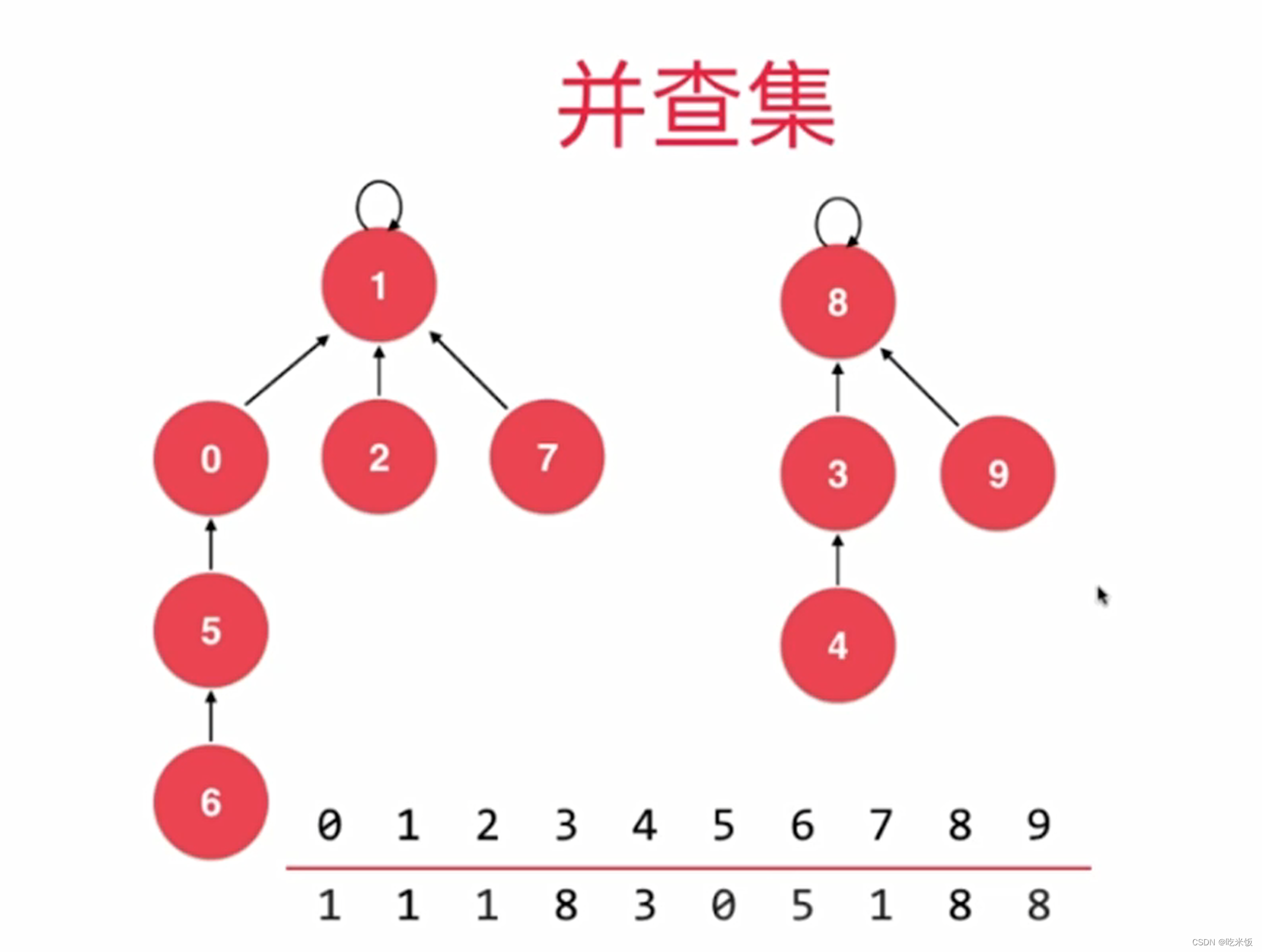
将每个元素,看做是一个节点,每个节点指向它的父节点,而根节点指向自己。如果我们进行unionElements(4,3)操作,那么就是让4索引的元素为3。同在一个树下面就是同一个集合表示相连。
#pragma once
#include "UF.h"
#include<cassert>
class UnionFind2 : public UF {
private:
int *parent;
int size;
public:
UnionFind2(int capacity) {
parent = new int[capacity];
size = capacity;
for (int i = 0; i < size; ++i) {
parent[i] = i;
}
}
const int getSize() const noexcept {
return size;
}
int find(int p) {
assert(p >= 0 && p < size);
while (p != parent[p]) {
p = parent[p];
}
return p;
}
bool isConnected(int p, int q) {
return find(p) == find(q);
}
void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
parent[pRoot] = qRoot;
}
};
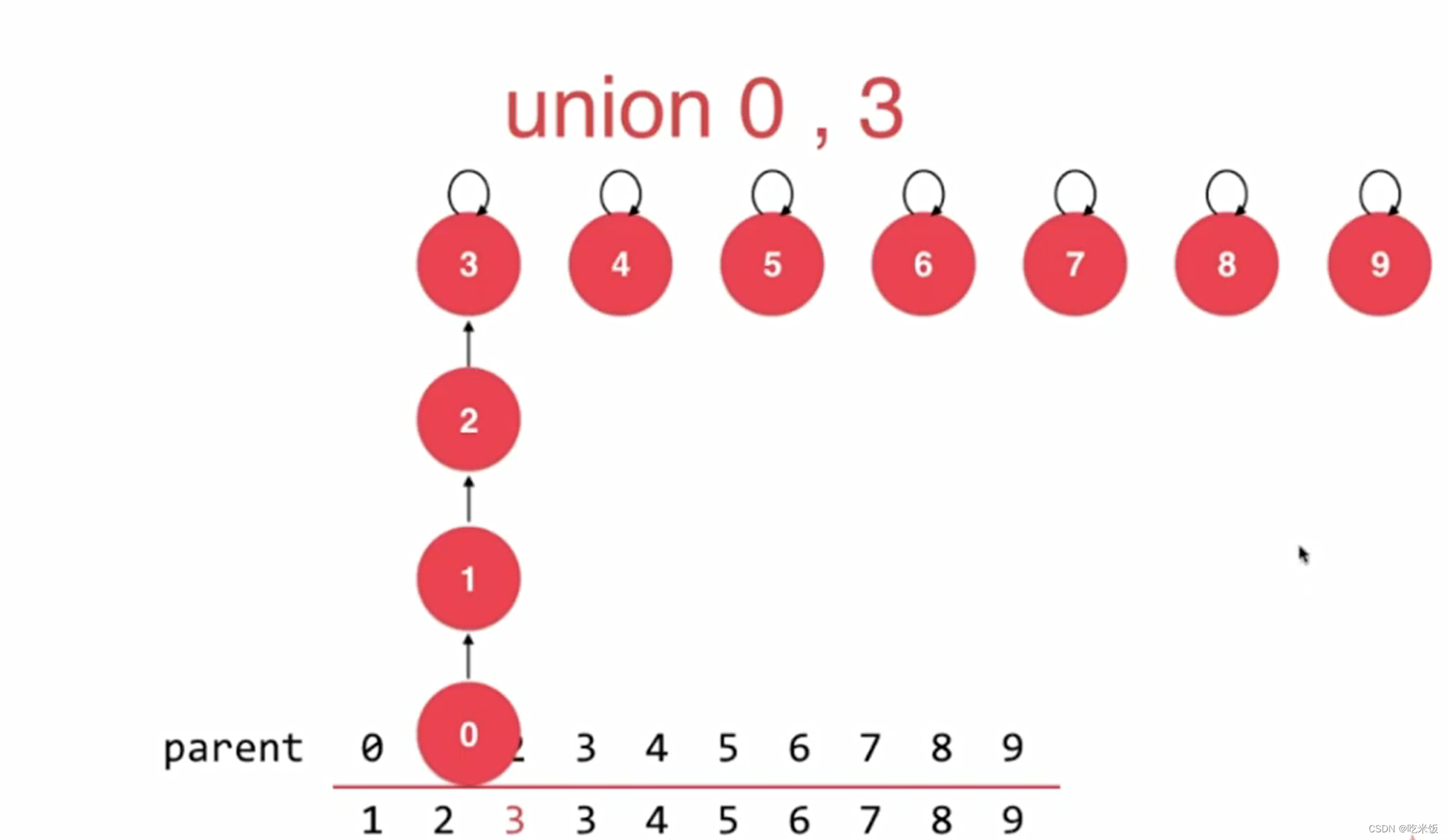
由于对真正合并那两个元素所在树的形状没有做判断,很多时候会增加树的高度。
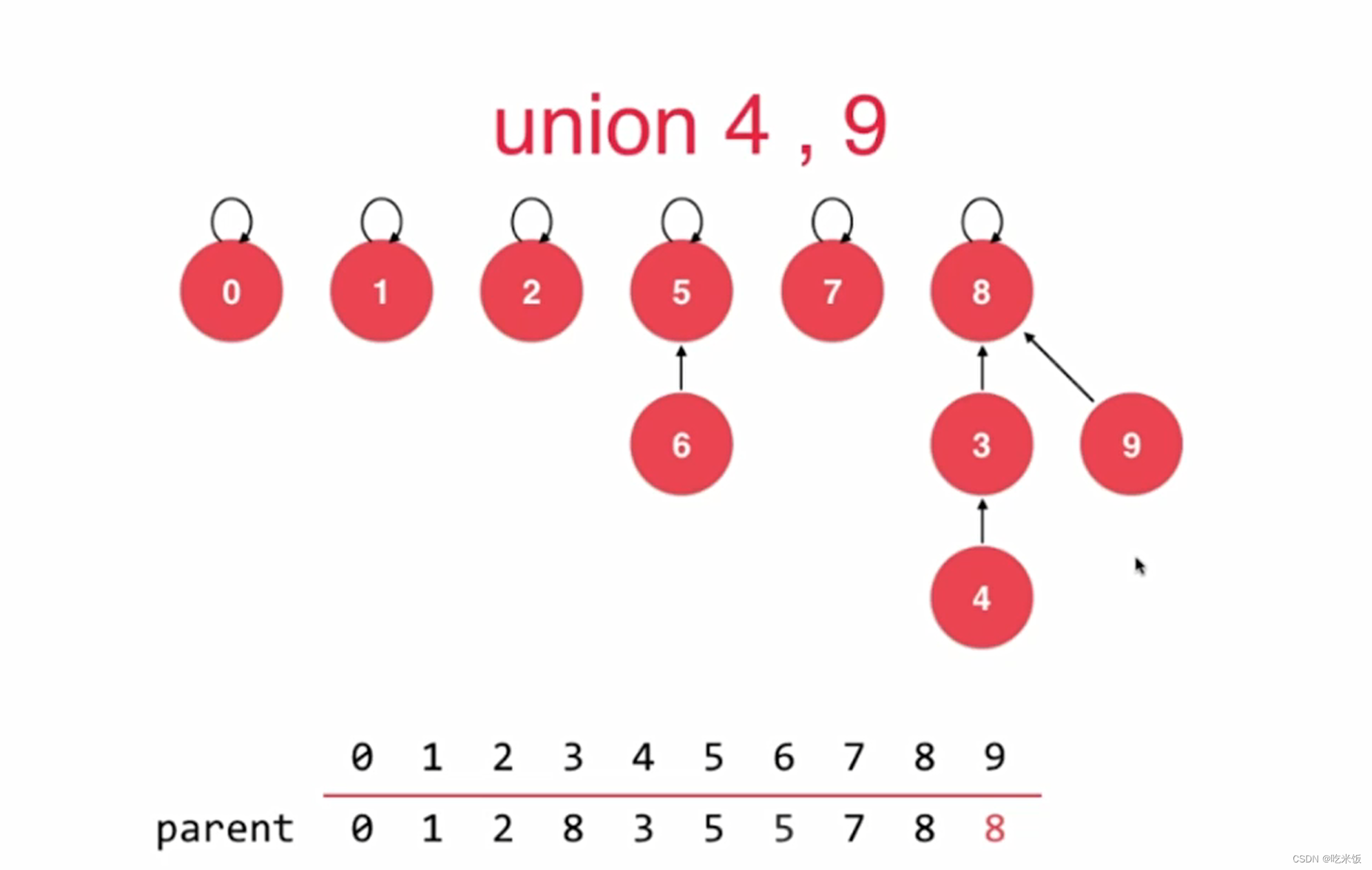
优化方法:节点个数小的那个节点去指向节点个数多个那个根节点。
#ifndef UNION_FIND_UNIONFIND3_H
#define UNION_FIND_UNIONFIND3_H
#include "UF.h"
#include <cassert>
class UnionFind3 : public UF {
private:
int *parent;
int *sz;
int size;
public:
UnionFind3(int capacity) {
parent = new int[capacity];
sz = new int[capacity];
size = capacity;
for (int i = 0; i < size; ++i) {
parent[i] = i;
sz[i] = 1;
}
}
int getSize() {
return size;
}
int find(int p) {
assert(p >= 0 && p < size);
while (p != parent[p]) {
p = parent[p];
}
return p;
}
bool isConnected(int p, int q) {
return find(p) == find(q);
}
void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
if (sz[pRoot] < sz[qRoot]) {
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
} else {
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
};
#endif //UNION_FIND_UNIONFIND3_H
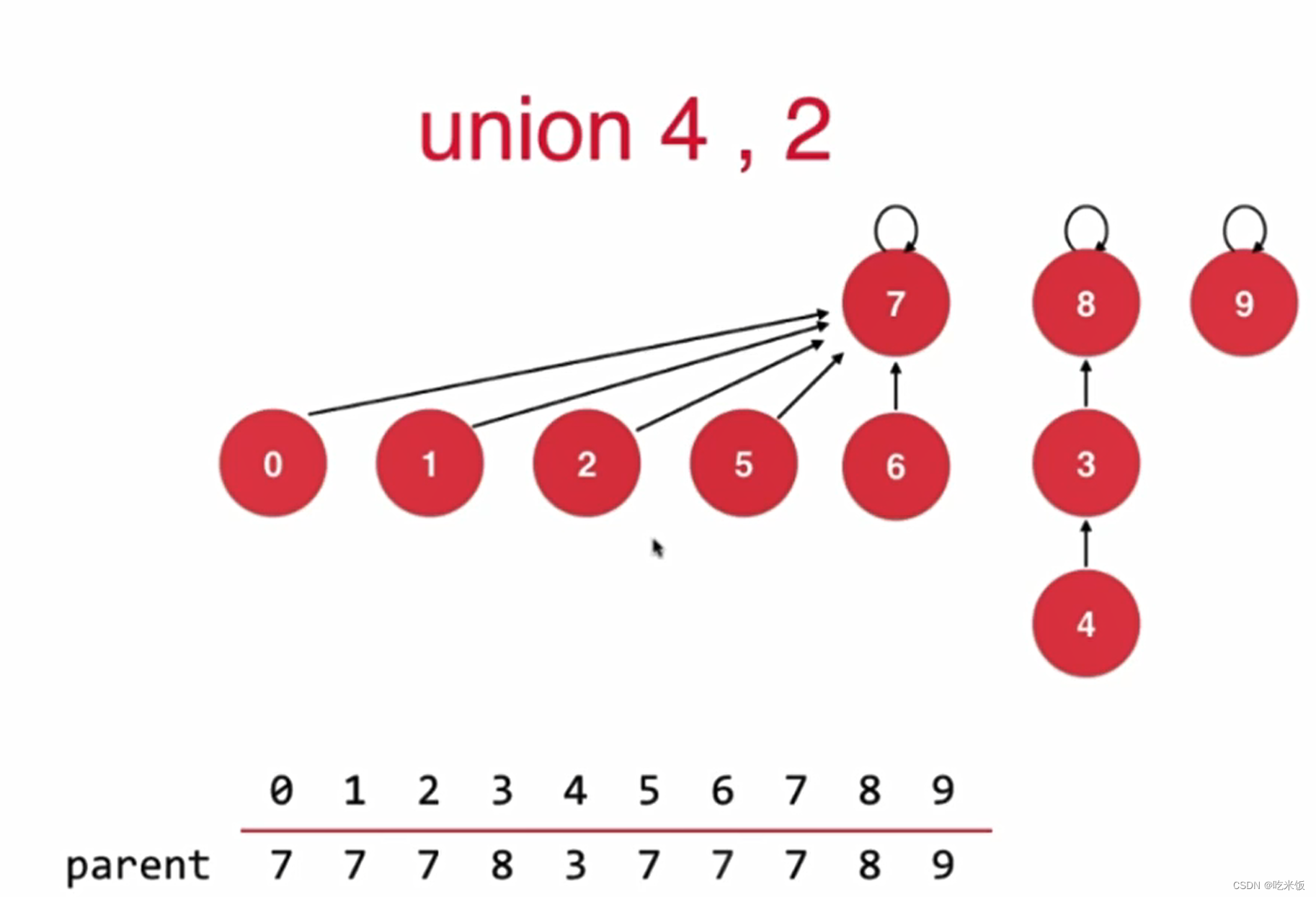
如果基于size优化会增加树的高度
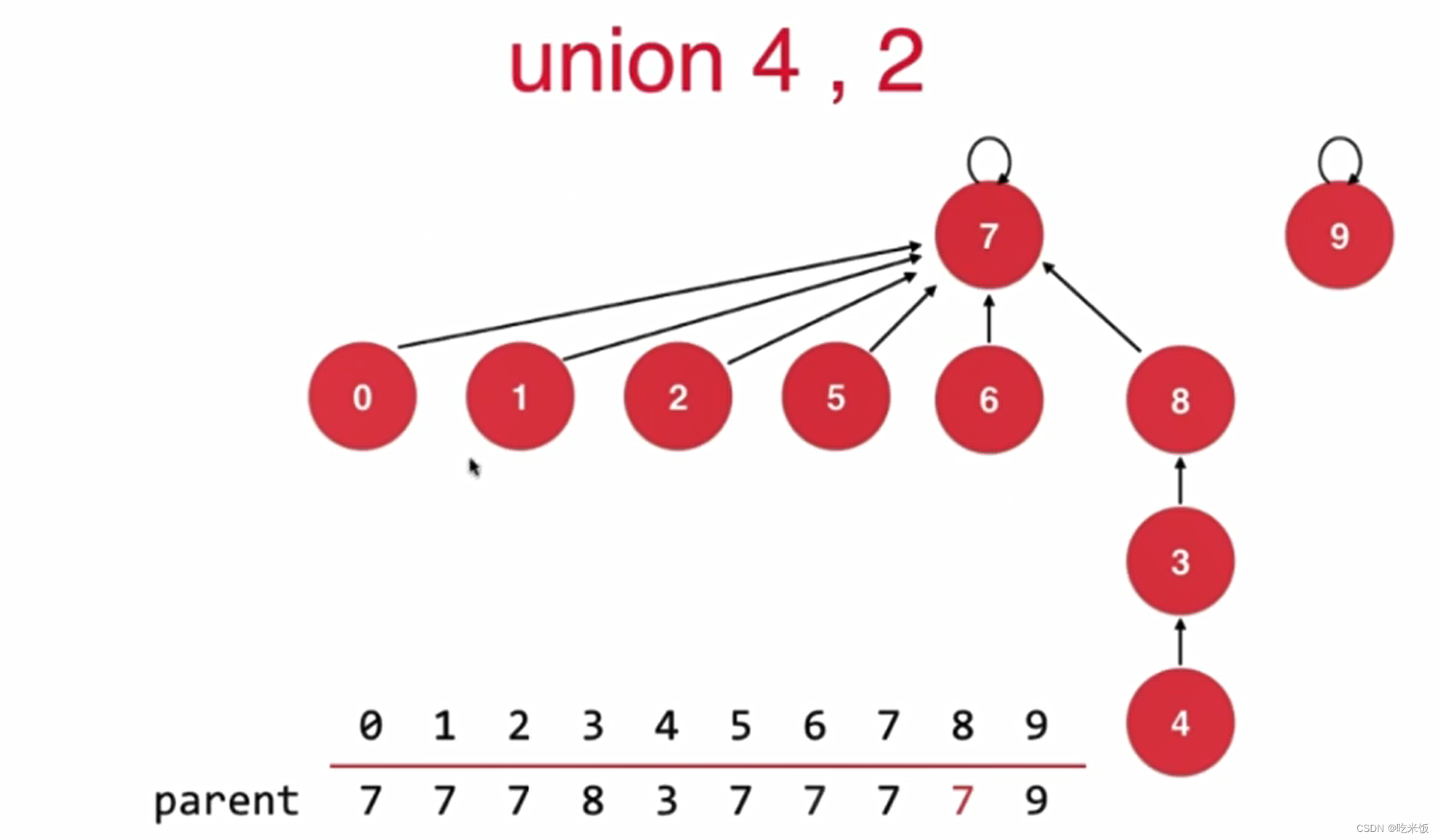
如果基于rank的优化rank[i]表示根节点为i的树的高度
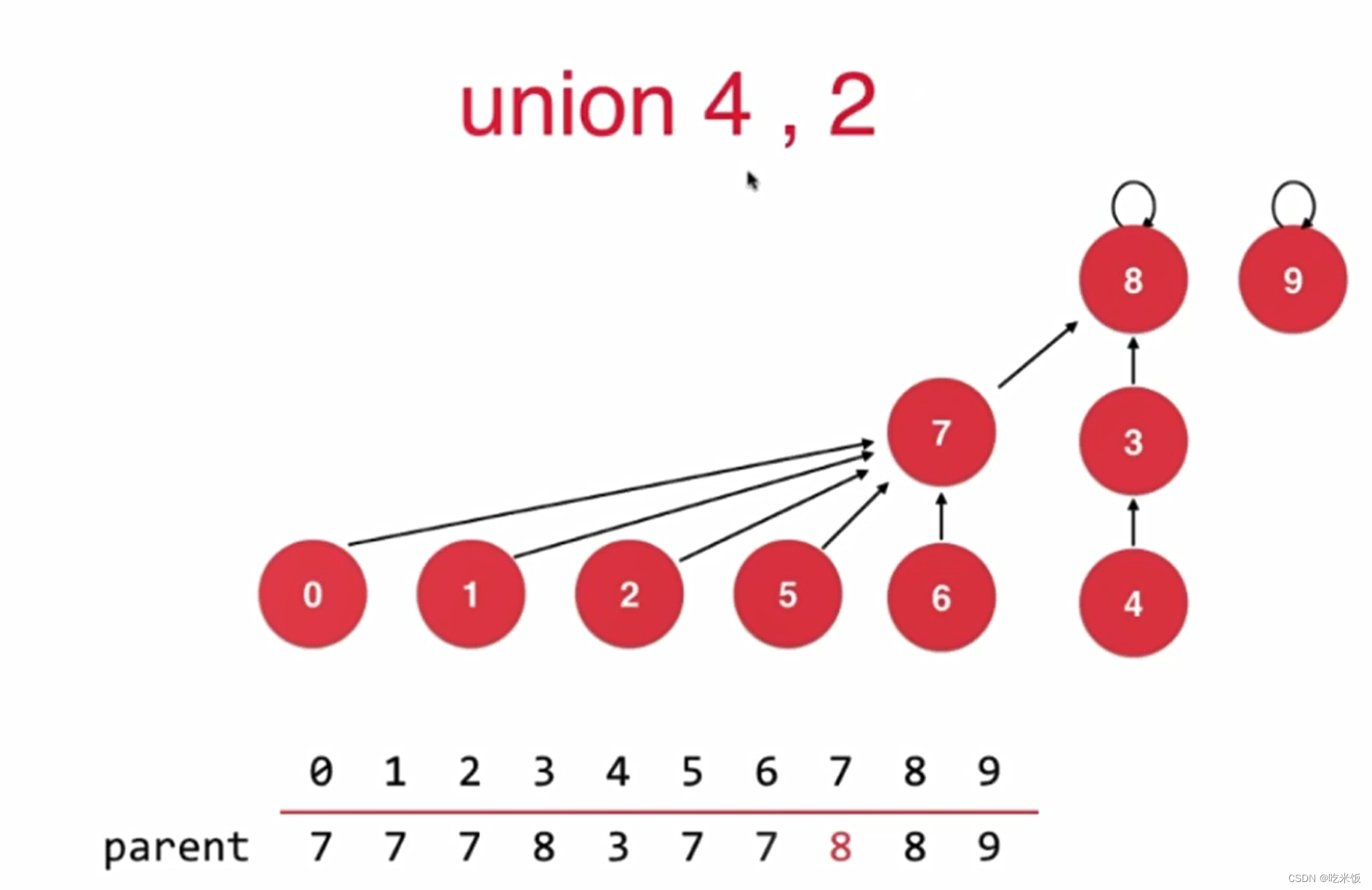
#ifndef UNION_FIND_UNIONFIND4_H
#define UNION_FIND_UNIONFIND4_H
#include "UF.h"
#include <cassert>
class UnionFind4 : public UF {
private:
int *parent;
int *rank;
int size;
public:
UnionFind4(int capacity) {
parent = new int[capacity];
rank = new int[capacity];
size = capacity;
for (int i = 0; i < size; ++i) {
parent[i] = i;
rank[i] = 1;
}
}
int getSize() {
return size;
}
int find(int p) {
assert(p >= 0 && p < size);
while (p != parent[p]) {
p = parent[p];
}
return p;
}
bool isConnected(int p, int q) {
return find(p) == find(q);
}
void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
if (rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot;
} else if (rank[pRoot] > rank[qRoot]) {
parent[qRoot] = pRoot;
} else {
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
};
#endif //UNION_FIND_UNIONFIND4_H
#pragma once
#include "UF.h"
#include<cassert>
class UnionFind : public UF {
public:
UnionFind(int cap) : size(cap) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; ++i) {
parent[i] = i;
rank[i] = 1;
}
}
~UnionFind() noexcept {
delete[] parent;
parent = nullptr;
}
const int getSize() const noexcept override {
return size;
}
//查询元素p和q是否在一个集合
bool isConnected(int p, int q) override {
return find(p) == find(q);
}
//合并元素p和q的集合
void unionElements(int p, int q) override {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
//就把其中一个的根节点挂到另一个的根上
if (rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot; //高度小的根节点指向高度大的根节点,从而减少树的高度,防止退化
} else if (rank[qRoot] < rank[pRoot]) {
parent[qRoot] = pRoot;
} else {
parent[qRoot] = pRoot;
++rank[pRoot];
}
}
private:
//查找元素p对应的集合编号,O(h)复杂度, h为树的高度
//根节点就是集合编号,且根节点指向自己,索引 p == parent[p]
int find(int p) {
assert(p >= 0 && p < size);
while (p != parent[p]) {
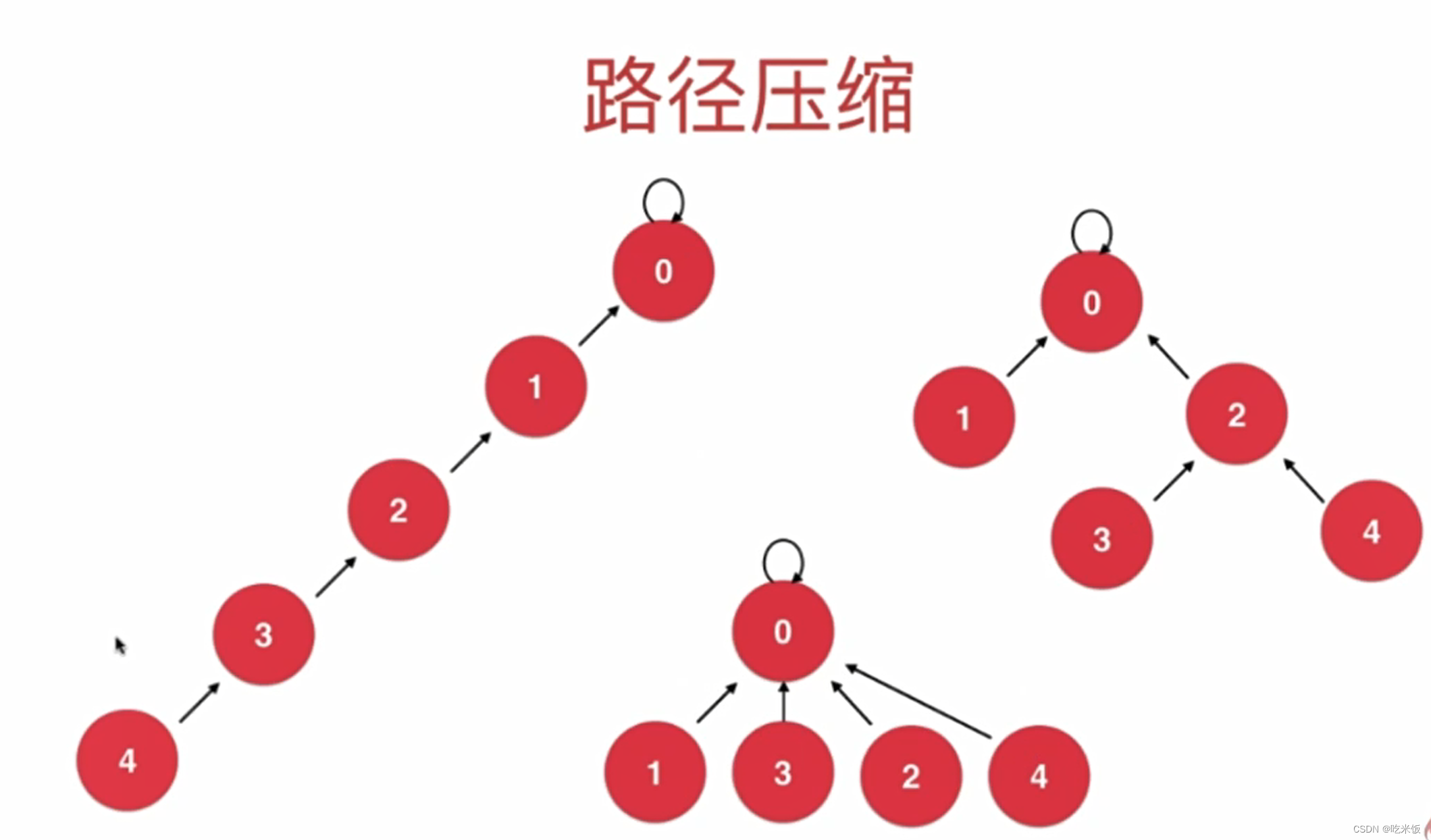
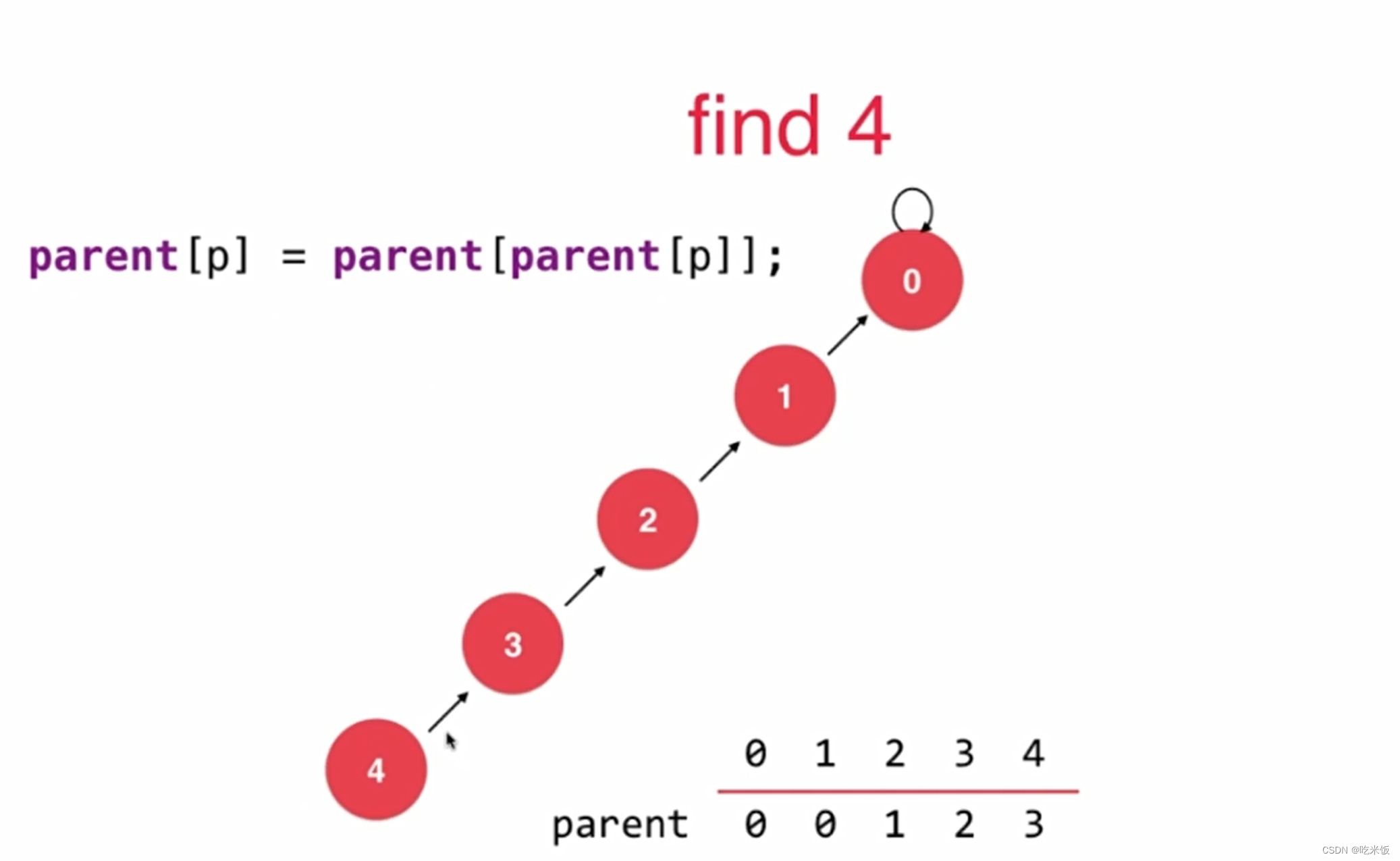
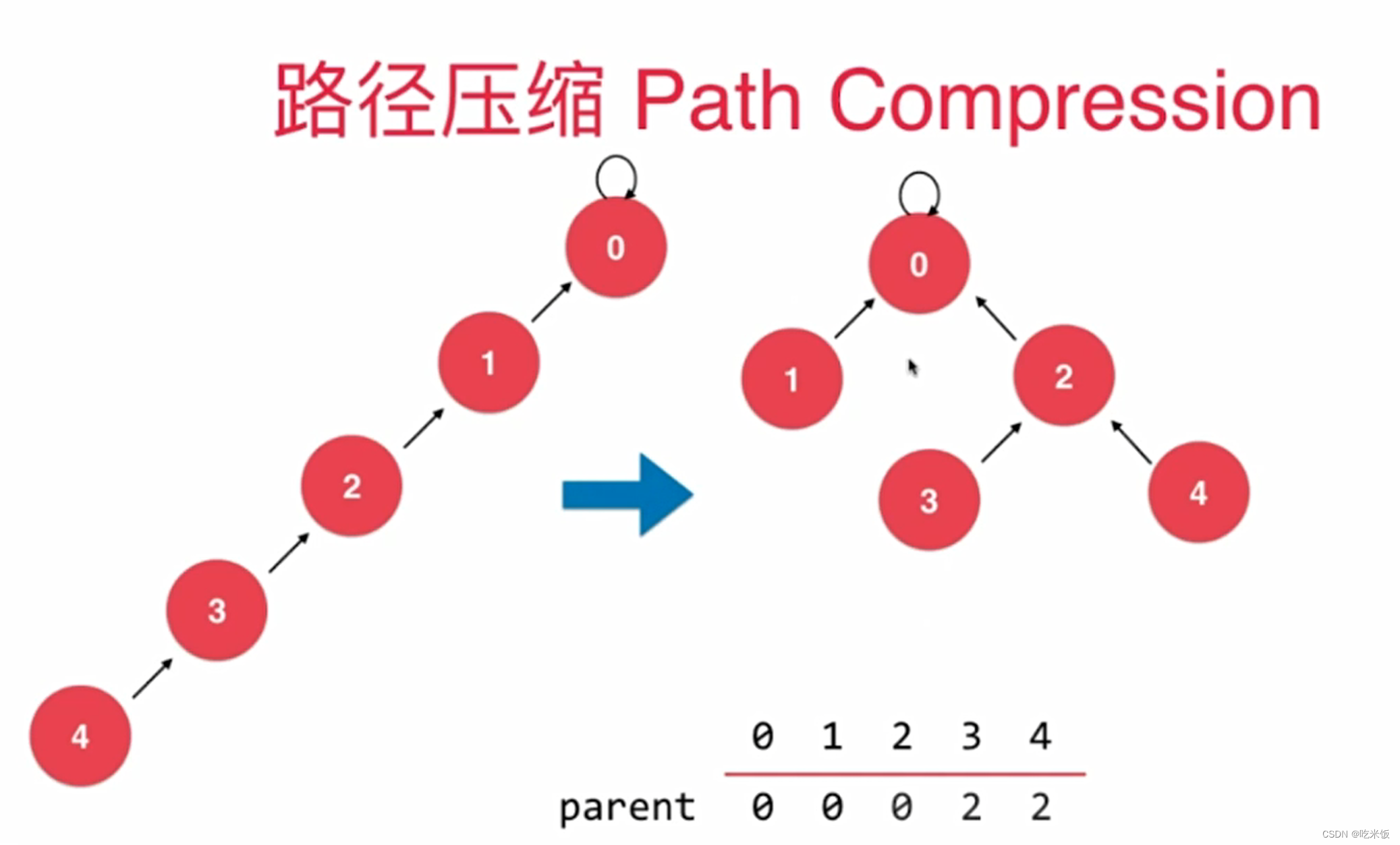
parent[p] = parent[parent[p]]; //路径压缩,让p这个节点指向它父亲的父亲
p = parent[p];
}
return p;
}
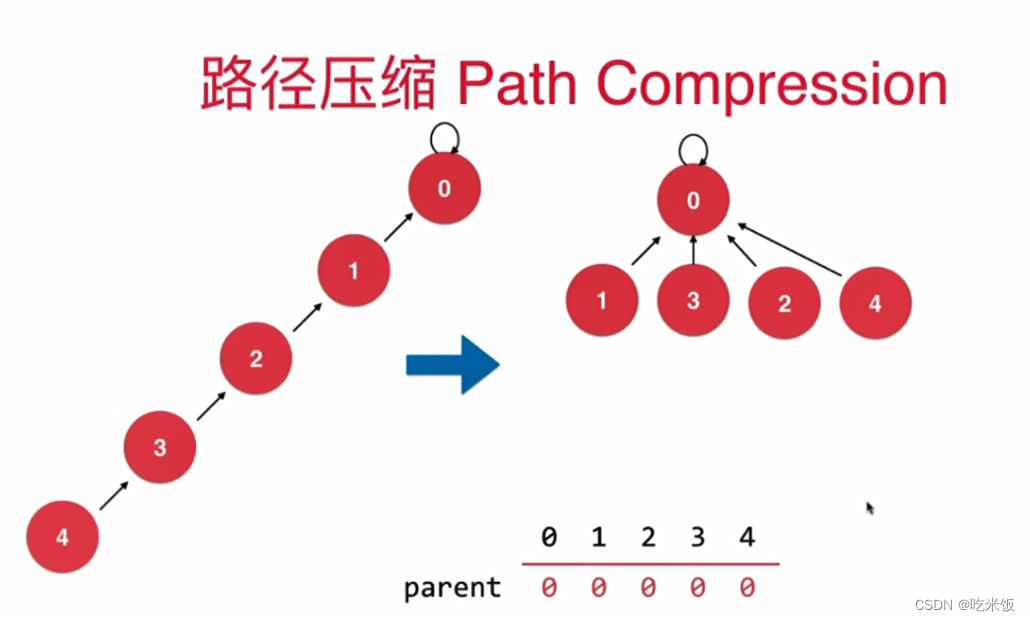
//递归版路径压缩,让集合中所有节点指向根节点
int recFind(int p) {
assert(p >= 0 && p < size);
if (p != parent[p]) {
parent[p] = find(parent[p]);
}
return parent[p];
}
private:
int *parent;
int *rank;
int size;
};
