排序算法之——归并排序分析

引言

接下来来分析第一个以最坏情形时间运行的算法——归并排序，它使用的比较次数也几乎是最优的，是递归算法的一个好的实例。

思路

基本操作时合并两个已排序的序列，若将输出放到第3个序列中，则该算法可以通过对输入数据一趟排序来完成。

• 序列一分为二
• 子序列递归排序
• 合并有序子序列

整个流程如下图所示：

其中，最复杂的是合并有序子序列这一步骤。为了简单，我们就拿上图逐层合并中倒数第二步来分析。

合并2,3,4,6和1,5,7,8这两个有序子序列。

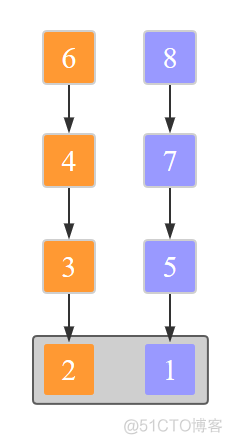
我们只需要关注这两个序列的首元素，从中挑选出较小的那一个元素放入辅助数组中。
此步将元素1移出原序列，放入辅助数组。

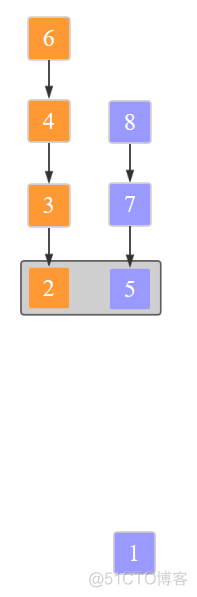
上图最下方的元素1位于辅助数组中。继续比较，将2放入辅助数组

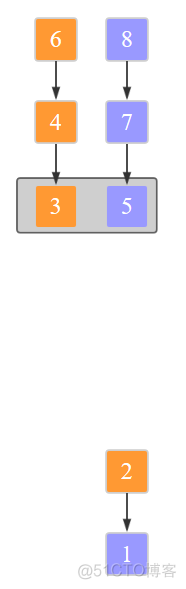
接下来直接贴一个完整的图：

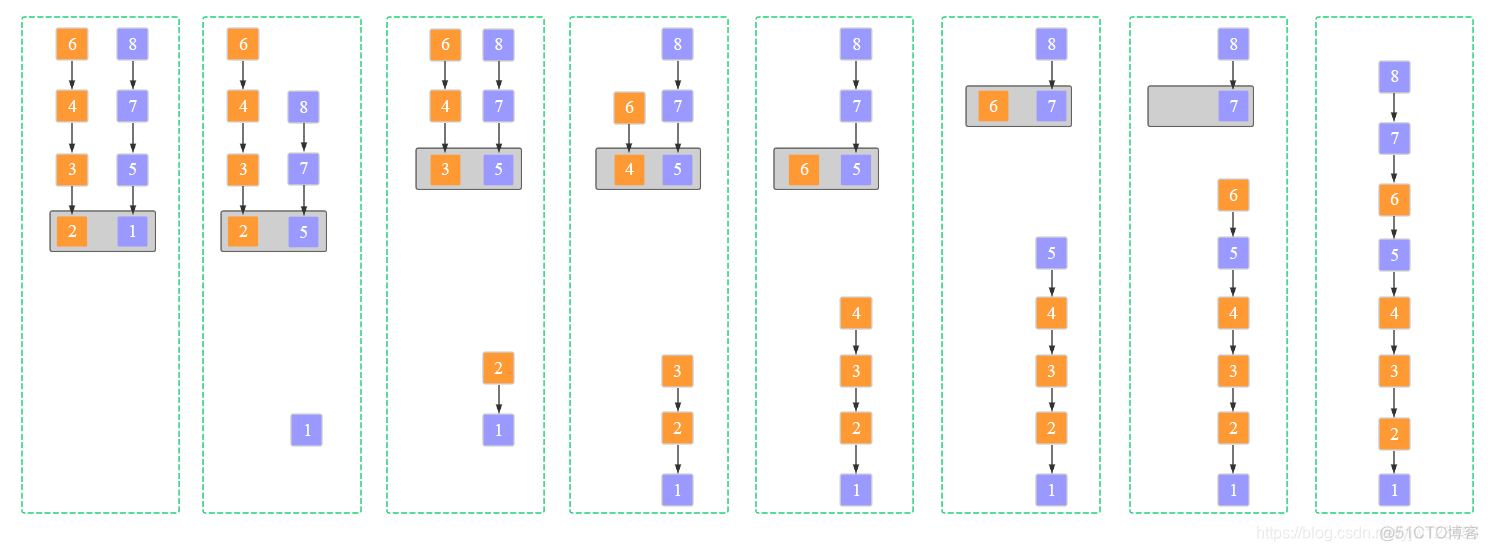
可以看到当某个子序列变空之后，直接将另一个子序列追加到辅助数组即可。

代码

public static <E extends Comparable<? super E>> void mergeSort(E[] array) {
mergeSort(array,0,array.length - 1);
}

private static <E extends Comparable<? super E>> void mergeSort(E[] array,int left,int right) {
if (left < right) {
int mid = left + (right - left) / 2;// (left + right)/2

/**
* 序列一分为二
* mid属于左边的数组，mid+1属于右边的数组
*/
mergeSort(array,left,mid);//对左子序列排序
mergeSort(array,mid + 1,right);//对右子序列排序

//优化：如果array[mid]小于array[mid+1],则不需要进行归并了
if (array[mid].compareTo(array[mid+1]) < 0) {
return;
}
// 归并
// 注意，传入的是mid+1
merge(array,left,mid+1,right);
}
}

/**
*
* @param array
* @param left 指向左边数组，左边数组开始位置
* @param right 指向右边数组，右边数组开始位置
* @param rightEnd 右边数组最后一个元素位置
*/
private static <E extends Comparable<? super E>> void merge(E[] array,int left, int right, int rightEnd) {
E[] aux = (E[]) new Comparable[array.length];//辅助数组

int leftEnd = right - 1;//左边数组最后位置
int auxIndex = left;//辅助数组开始位置
int num = rightEnd - left + 1;//元素总数
while (left <= leftEnd && right <= rightEnd) {
//比较两个序列的首元素
if (array[left].compareTo(array[right]) <0) {
aux[auxIndex++] = array[left++];
} else {
aux[auxIndex++] = array[right++];
}
}

/**
* 拷贝剩下的元素
* 以下两个while循环，只有一个会执行
*/
while (left <= leftEnd) {
aux[auxIndex++] = array[left++];
}
while (right <= rightEnd) {
aux[auxIndex++] = array[right++];
}
//将辅助数组拷贝回原数组，注意是逆序的方式
for (int i = 0; i < num; i++,rightEnd --) {
array[rightEnd] = aux[rightEnd];
}
}

复杂度和稳定性

• 时间复杂度

原序列长度为N，则细分得最大深度为;每一层需要排序的元素为N,则归并排序的时间复杂度为

• 稳定性

因为交换元素时，大小相等的情况下可以不交换，所以归并排序是稳定的；