你真的懂01背包问题吗？01背包的这几问你能答出来吗？

本篇文章主要带大家从0开始剖析01背包问题，主要分享一些基本但经常被忽略的问题，比如for循环的顺序，数组空间优化问题的原理，用一维数组解决01背包问题！ 你真的懂01背包问题吗？01背包的这几问你能答出来吗？ 关于01背包的几个问题

• 背包问题的动态转移方程是怎么来的？

• 你能解释背包问题的两个for循环的意义嘛？

• 为什么需要两个for循环，一个循环行不行？

• 01背包问题的for循环一定要从0开始吗？

• 01背包滚动数组的优化原理是什么？

• 01背包只用不用二维数组只用一位数组的依据是什么？

这些问题在阅读完本文之后你将会得到答案！

01背包问题介绍

有 \(N\)件物品和一个容量是 \(V\) 的背包。每件物品只能使用一次。第\(i\)件物品的体积是\(v_i\)，价值是 \(w_i\)。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

比如下面的4个物品，背包能够承受的最大重量为5，我们应该如何选择，使得我们获得的总价值最大：

物品 重量 价值 A 1 2 B 2 4 C 3 4 D 4 5

这个问题还是比较简单，我们直接看就知道选择物品B和物品C得到的价值最大。那么我们如何设计一个算法去实现这个问题呢？首先对于每一个物品都有两种情况，选择和不选择，我们需要选择两种情况当中能够获取最大价值的那种情况。

01背包问题动态转移方程

首先我么先要确定一个信息就是没件物品只有一件，选完就没有了。如果我们的背包当中还有剩余容量可以放下某个物品，那么对于这个物品我们就有两种选择：选或者不选。

我们定义数组dp[i][j]，其含义是对于前i件物品，在我们的背包容量为j的情况下我们能够获得的最大的收益，如果我们有N件物品，背包容量为V，那么我们能够获得的最大价值为dp[N][V]，因为他表示的是对于前N个物品，在背包容量为V的情况下我们能够获取到的最大的价值。我们可以得到下面的公式：

\[dp[i][j]=max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j])，如果背包的容量大于等于物品 i 占的体积 \]

\[dp[i][j]=dp[i - 1][j]，如果背包的容量小于物品 i 占的体积 \]

• 第一种情况（背包容量大于等于第i件物品的体积v[i]时）：
  • 在这种情况下我们对于第i件物品有两种选择，一种是将其放入背包当中，另外一种就是不选他，那么我们就可以使用容量为j的背包在前i-1件物品进行选择。
  • 如果我们选第i件物品，那么我们背包剩下的容量就为j - v[i]，我们还能选择的物品就是前i - 1个物品，这个情况下能够获得的最大的收益为\(dp[i - 1][j - v[i]]\)，再加上我们选择的第i件物品的价值，我们选择第i件物品能够获得的总收益为dp[i - 1][j - v[i]] + w[i]。
  • 如果我们不选择第i件物品，那么我们背包剩余容量仍然为j，而且我们只能从前i - 1 个商品当中进行选择，那么我们最大的收益就为dp[i - 1][j]。
• 第二种情况（背包容量小于第i件物品的体积v[i]时）：
  • 这种情况下我们只能够选择前i - 1个商品，因此我们能够获取的最大收益为dp[i - 1][j]。

01背包数据依赖问题分析

在上文当中我们已经分析出来了我们的动态转移方程：

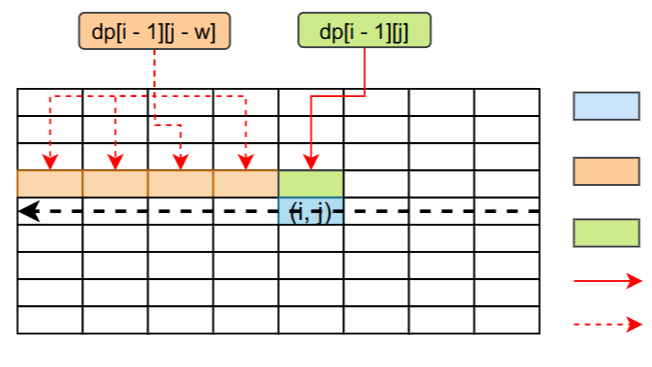
\[dp[i][j]=max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j])，如果背包的容量大于等于物品 i 占的体积 \]

\[dp[i][j]=dp[i - 1][j]，如果背包的容量小于物品 i 占的体积 \]

根据上面两个公式分析，我们知道要想解出dp[i][j]的值，我们首先需要知道dp[i - 1][j - v[i]]的值和dp[i - 1][j]的值，他们之间的依赖关系如下图所示：

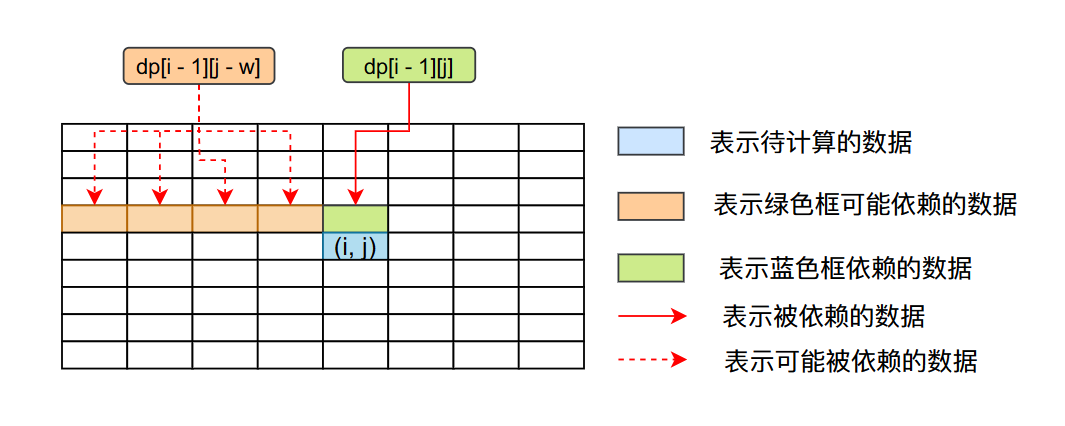
基于上面的数据依赖关系，我们知道我们如果想求dp[N][V]的值，首先要求出dp数组第N - 1行的所有的值，因为dp[N][V]依赖dp[N - 1][V]，而且可能依赖dp[N - 1][i]的值（i大于等于0，小于V），而dp[N - 1][V]又依赖dp[N - 2][V]......
根据上面的分析过程，如果我们想计算出dp[N][V]的结果，那就需要从第1行开始往后计算，一直算到第N`行，因此我们可以写出下面的代码：

Java版本：

import java.util.Scanner;

public class Main {

  public static int backpack(int[] w, int[] v, int N, int V) {
    int[][] dp = new int[N + 1][V + 1];
    // 初始化
    for (int i = v[1]; i <= V; ++i) {
      dp[1][i] = w[1];
    }
    // 第一行已经初始化 从第二行开始
    for (int i = 2; i <= N; ++i) {
      for (int j = 0; j <= V; ++j) {
        if (j >= v[i])
          dp[i][j] = Math.max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]);
        else
          dp[i][j] = dp[i - 1][j];
      }
    }
    return dp[N][V];
  }

  public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int N = scanner.nextInt();
    int V = scanner.nextInt();
    int[] w = new int[N + 1];
    int[] v = new int[N + 1];
    for (int i = 1; i <= N; i++) {
      v[i] = scanner.nextInt();
      w[i] = scanner.nextInt();
    }
    System.out.println(backpack(w, v, N, V));
  }
}

C++版本：

#include <iostream>
using namespace std;

#define L 20000
int w[L]; // 物品价值
int v[L]; // 物品体积
int dp[L][L];

int N; // 物品数量
int V; // 背包的体积

int backpack() {

	// 初始化
	for (int i = v[1]; i <= V; ++i) {
		dp[1][i] = w[1];
	}
	// 第一行已经初始化 从第二行开始
	for (int i = 2; i <= N; ++i) {
		for (int j = 0; j <= V; ++j) {
			if (j >= v[i])
				dp[i][j] = max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]);
			else
				dp[i][j] = dp[i - 1][j];
		}
	}
	return dp[N][V];
}

int main() {
	cin >> N >> V;
	for (int i = 1; i <= N; ++i) {
		cin >> v[i] >> w[i];
	}
	cout << backpack();
	return 0;
}

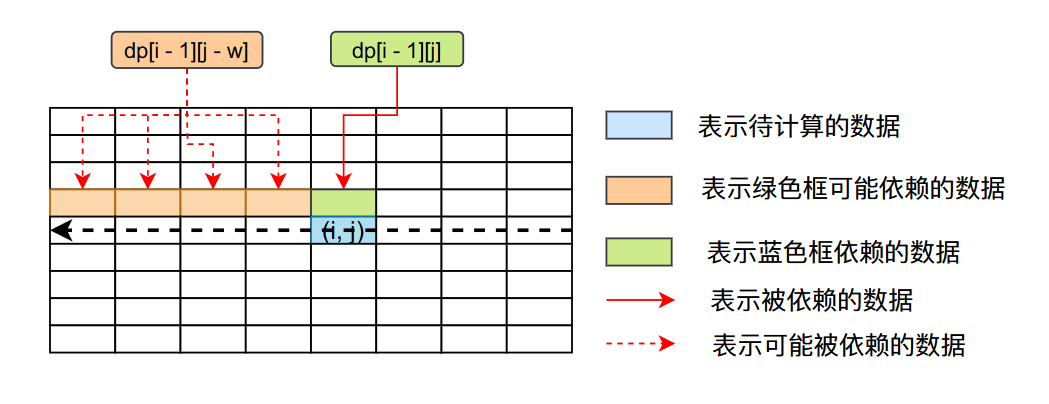
从上图看我们在计算第i的数据的时候我们只依赖第i - 1行，我们在第i行从后往前遍历并不会破坏动态转移公式的要求。

因此下面的代码也是正确的：

public static int backpack(int[] w, int[] v, int N, int V) {
    int[][] dp = new int[N + 1][V + 1];
    // 初始化
    for (int i = v[1]; i <= V; ++i) {
        dp[1][i] = w[1];
    }
    // 第一行已经初始化 从第二行开始
    for (int i = 2; i <= N; ++i) {
        // 这里是从末尾到0
        // 前面是从0遍历到末尾
        for (int j = V; j >= 0; --j) {
            if (j >= v[i])
                dp[i][j] = Math.max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]);
            else
                dp[i][j] = dp[i - 1][j];
        }
    }
    return dp[N][V];
}

01背包问题优化——滚动数组

我们在解决背包问的时候我们是开辟了一个二维数组dp，那么我们能不能想斐波拉契数列那样降低算法的空间复杂度呢？我们已经很清楚了我们在计算dp数据的时候进行计算的时候只使用了两行数据，那么我们只需要申请两行的空间即可，不需要申请那么大的数组空间，计算的时候反复在两行数据当中交替计算既可。比如说我们已经计算好第一行的数据了（初始化），那么我们可以根据第一行得到的结果得到第二行，然后根据第二行，将计算的结结果重新存储到第一行，如此交替反复，像这种方法叫做滚动数组。

下面的代码当中dp数组是从第0行开始使用的，前面的代码是从第一行开始的。

import java.util.Scanner;

public class Main {


    public static int backpack(int[] v, int[] w, int V) {
      int N = w.length;
      int[][] dp = new int[2][V + 1];
      for (int i = v[0]; i < V; ++i) {
        dp[0][i] = w[0];
      }
      for (int i = 1; i < N; ++i) {
        for (int j = V; j >= 0; --j) {
          if (j >= v[i])
            dp[i % 2][j] = Math.max(dp[(i - 1) % 2][j],
                dp[(i - 1) % 2][j - v[i]] + w[i]);
          else
            dp[i % 2][j] = dp[(i - 1) % 2][j];
        }
      }
      return dp[(N - 1) % 2][V];
  }


  public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int N = scanner.nextInt();
    int V = scanner.nextInt();
    int[] w = new int[N];
    int[] v = new int[N];
    for (int i = 0; i < N; i++) {
      v[i] = scanner.nextInt();
      w[i] = scanner.nextInt();
    }
    System.out.println(backpack(v, w, V));
  }
}

背包空间再优化——单行数组和它的遍历顺序问题

我们还能继续压缩空间吗