面试官：完全背包都不会，是你自己走还是我送你？

带你从0开始深入剖析完全背包问题，分析动态规划问题的套路，从0设计动态转移方程，带你优化数组空间！！！ 面试官：完全背包都不会，是你自己走还是我送你？

在如今的面试当中算法题已经成为面试不可或缺的内容，今天就跟大家分享一个还比较困难的笔试题——完全背包。

完全背包问题

有\(N\)种物品和一个容量是 \(V\)的背包，每种物品都有无限件可用。第\(i\) 种物品的体积是 \(v_i\)，价值是\(w_i\)。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

完全背包问题和01背包的唯一区别就在于物品的个数，在01背包当中所有的物品只有一件，也就只能使用一次。而在完全背包当中物品可以使用无限多次。

比如下面的4个物品，背包能够承受的最大重量为5，我们应该如何选择，使得我们获得的总价值最大：

物品 重量 价值 A 1 2 B 2 4 C 3 4 D 4 5

这个问题还是比较简单，我们直接从图中看，我们可以选择五个A或者两个B一个A，可以产生最大的收益，最大收益为10。

完全背包问题分析 01背包动态转移方程分析

在01背包问题当中，我们是使用一个二维数组dp[i][j]进行计算，dp[i][j]表示在只使用前i个物品且背包容量为j的情况下，我们能够获得的最大的收益。在这个情况下，我们根据当前背包容量j判断是否能装入第i个物品可以得到下面两个方程（下面公式字母的含义与上文完全背包问题所提到的一致）。

\[dp[i][j] = \begin{cases} max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]), j \ge v[i]\\ dp[i - 1][j] , j \lt v[i] \end{cases} \]

上面01背包的公式的第二条比较简单，如果背包容量不足以容纳第i件物品，那么只能从前i - 1物品当中选择了。我们来仔细分析一下第一条公式。

如果当前背包容量可以容纳第i个物品，那么我们就可以选择第i件物品或者不选择，我们应该选择两种选择当中收益更大的那个。

• 如果我们不选择第i个物品，那么我们就能够使用容量为j的背包去选择前i - 1个物品，这种情况下我们的最大收益为dp[i - 1][j]。
• 如果选择第i个物品，那么我们背包容量还剩下j - v[i]，还可以选择剩下的i - 1个物品，而且我们的收益需要加上w[i]，因此我们的收益为max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j])。

完全背包动态转移方程分析

和01背包问题一样首先对于第i个物品，首先需要判断背包是否能够容纳：

• 如果背包的容量大于等于第i个物品的体积，那我们就有两种选择：
  • 将第i个物品放入背包当中，但是在这里需要注意的一点是完全背包的物品有无数件，因此当我们选择之后我们的转移方程为dp[i][j - v[i]] + w[i]，这里不是i-1而是i，因为第i件物品有无数件。
  • 不将第i个物品放入背包当中，那么我们就能够使用容量为j的背包去选择前i - 1个物品，这种情况下我们的最大收益为dp[i - 1][j]。
• 如果背包容量小于第i件物品的体积，我们就不能够选择第i件物品了，这种情况下我们的最大收益为dp[i - 1][j]。

基于上面的分析我们可以知道完全背包问题的动态转移方程为：

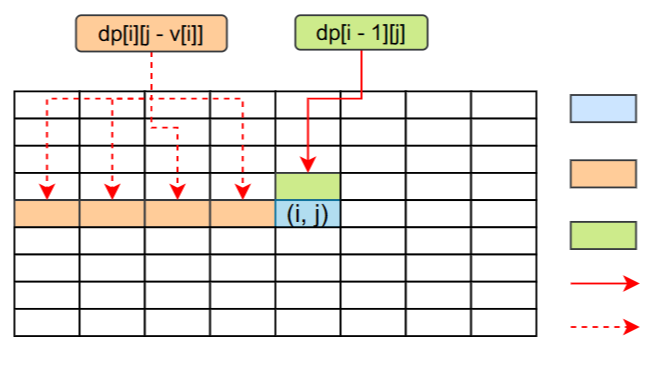
\[dp[i][j] = \begin{cases} max(dp[i][j - v[i]] + w[i], dp[i - 1][j]), j \ge v[i]\\ dp[i - 1][j] , j \lt v[i] \end{cases} \]

背包问题代码构成设计

根据对动态转移方程的分析，我们可以知道，我们在计算dp[i][j]这个数据的值的时候，我们首先需要将dp[i][j - v[i]]和dp[i - 1][j])的结果计算出来，因为dp[i][j]依赖这两个数据。

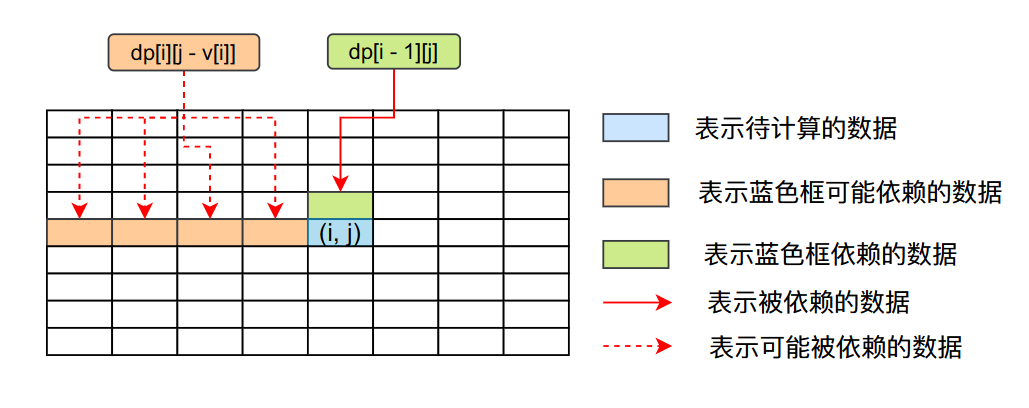
根据上面的分析和图我们知道，在计算dp[i][j]之前，我们需要将第i行第j列之前的数据和dp[i - 1][j]都计算出来，因为dp[i][j]依赖这些数据。而我们最终需要的结果是dp[N][V]表示在背包容量为V且能够选择前N个物品（也就是所有物品）能够获得的最大的收益，所以我们最终需要求出dp[N][V]的值。

因此基于以上分析，我们要想最终解出dp[N][V]的值，我们可以采取两重for循环，第一重循环遍历物品，第二重循环遍历容量，但是我们的第0行没有前一行，因此我们需要对第0行进行初始化：

// 对第0行进行初始化操作
for (int i = 0; i <= V; ++i) {
    // 如果只能选择第一个数据，而且能选无数次
    // 那就将所有的容量都拿来装第一个物品
    dp[0][i] = i / v[0] * w[0];
}

根据动态转移方程，我们有下面的代码：

for (int i = 1; i < N; ++i) {
    for (int j = 0; j <= V; ++j) {
        if (j >= v[i]) {
            dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
        }
        else {
            dp[i][j] = dp[i - 1][j];
        }
    }
}

C++完整代码如下：

#include <iostream>
using namespace std;
#define MAX_LEN 10000

int w[MAX_LEN];
int v[MAX_LEN];
int dp[MAX_LEN][MAX_LEN];
int N, V;

int backpack() {
	// 对第0行进行初始化操作
	for (int i = 0; i <= V; ++i) {
		// 如果只能选择第一个数据，而且能选无数次
		// 那就将所有的容量都哪来装第一个物品
		dp[0][i] = i / v[0] * w[0];
	}
	for (int i = 1; i < N; ++i) {
		for (int j = 0; j <= V; ++j) {
			if (j >= v[i]) {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
			}
			else {
				dp[i][j] = dp[i - 1][j];
			}
		}
	}
	return dp[N - 1][V];
}

java代码如下：

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int N = scanner.nextInt();
    int V = scanner.nextInt();
    int[] w = new int[N];
    int[] v = new int[N];
    int[][] dp = new int[N][V + 1];
    for (int i = 0; i < N; i++) {
        v[i] = scanner.nextInt();
        w[i] = scanner.nextInt();
    }

    // 对第0行进行初始化操作
    for (int i = 0; i <= V; ++i) {
        // 如果只能选择第一个数据，而且能选无数次
        // 那就将所有的容量都哪来装第一个物品
        dp[0][i] = i / v[0] * w[0];
    }

    for (int i = 1; i < N; ++i) {
        for (int j = 0; j <= V; ++j) {
            if (j >= v[i]) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
            }
            else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    System.out.println(dp[N - 1][V]);
}

完全背包数组优化

在前面的内容当中我们已经仔细分析了完全背包问题的动态转移方程，我们发现在两层循环的内层循环当中，必须从0遍历到V，因为我们后面的数据依赖同一行前面的数据，还有就是依赖上一行相同列的数据，比如dp[i][j]依赖dp[i][0]到dp[i][j - 1]，还依赖dp[i - 1][j]，这个其实是可以只用一个数组进行计算的。

我们先来看单行完全背包的Java代码：

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int N = scanner.nextInt();
    int V = scanner.nextInt();
    int[] w = new int[N];
    int[] v = new int[N];
    int[] dp = new int[V + 1];

    for (int i = 0; i < N; i++) {
        v[i] = scanner.nextInt();
        w[i] = scanner.nextInt();
    }

    for (int i = 0; i < N; i++) {
        for (int j = v[i]; j <= V; j++) {
            dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    System.out.println(dp[V]);
}

下面我们举个使用单行数组优化的例子：

假如我们正在更新dp[j]，此时dp[j]还是第i-1行的状态而dp[0]到dp[j-1]已经是第i行的状态了，因为我们是从前到后进行遍历。而要计算dp[j]的第i行状态的结果，那么他需要dp[0]到dp[j-1]的第i行状态的数据，dp[j]的第i-1行状态的数据，而实际情况数组能够满足这种依赖关系，因此我们可以使用单行数组优化。

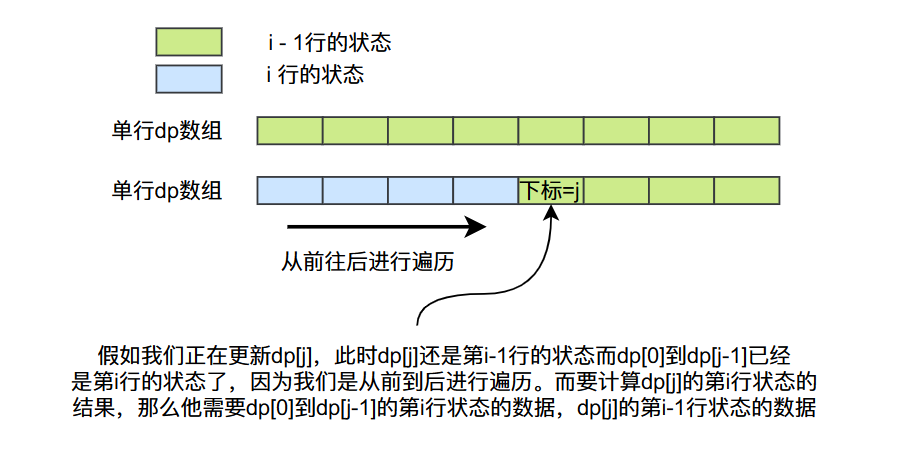
这个单行数组与多行数组的区别是多行数组每一行有每一行的状态，而且他保存了所有行的状态，单行数组只存在一行的状态，但是他会经历所有行的状态，也就是在外层for循环下单行数组的状态不断更新。（如果你不理解这段话和上面谈到的单行数组优化，可以结合代码和文字进行理解）

C++代码：

#include <iostream>
using namespace std;
#define MAX_LEN 10000

int w[MAX_LEN];
int v[MAX_LEN];
int dp[MAX_LEN]
int N, V;

int backpack() {
	for (int i = 0; i < N; ++i) {
		for (int j = v[i]; j <= V; ++j) {
			dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
		}
	}
	return dp[V];
}

int main() {

	cin >> N >> V;
	for (int i = 0; i < N; ++i) {
		cin >> v[i] >> w[i];
	}
	cout << backpack();
	return 0;
}

总结

在仔细分析完完全背包问题之后，我们可以总结一下动态规划的套路：

• 分析问题设置dp数组并分析数组的含义。
• 寻找动态转移方程，分析dp数组当中数据之间的依赖关系，我们在迭代的时候一定要遵循这个关系。
• 初始化数组。
• 进行数组dp求解。
• 分析动态转移方程的含义和数据依赖关系，分析是否能够在不破坏数据依赖关系的条件下，优化数组空间。

其实上面的套路对于大多数动态规划的题目都有用的，因为动态规划的流程基本一致，而动态规划最难的地方就是第一步了，通过分析问题寻找动态转移方程。

以上就是本篇文章的所有内容了，希望大家有所收获，我是LeHung，我们下期再见！！！

---

更多精彩内容合集可访问项目：https://github.com/Chang-LeHung/CSCore

关注公众号：一无是处的研究僧，了解更多计算机（Java、Python、计算机系统基础、算法与数据结构）知识。