莫比乌斯函数

目录

• ​​前导​​

• ​​积性函数​​

• ​​莫比乌斯函数​​
• ​​莫比乌斯反演​​

• ​​莫比乌斯反演定理​​
• ​​莫比乌斯反演定理证明​​
• ​​莫比乌斯反演另一性质(与欧拉函数有关)​​

前导

要学习莫比乌斯函数 需要学习 到 积性函数，深度理解欧拉筛。

先说说什么是积性函数吧。

积性函数

其实积性函数非常好理解，
定义

积性函数：若gcd(a,b)=1，且满足f(ab)=f(a)f(b)，则称f(x)为积性函数
完全积性函数：对于任意正整数a，b，都满足f(ab)=f(a)f(b)，则称f(x)为完全积性函数
性质

1.若f(n),g(n)均为积性函数，则函数h(n)=f(n)g(n)也是积性函数
2.若f(n)为积性函数，则函数c*f(n)(c是常数)也是积性函数，反之一样
3.任何积性函数都能应用线性筛，在O(n)时间内求出1~n项(莫比乌斯就要用到)，像素数，欧拉函数等都是 积性函数。

知道这些之后，我们就来看莫比乌斯函数。

莫比乌斯函数

定义：

莫比乌斯函数主要是个分段函数。

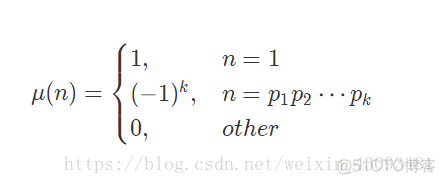
性质：

1.对于任意正整数n，

2.对于任意正整数n，

强烈建议 ： 深度理解完这两条性质之后，在去看莫比乌斯反演，要不莫比乌斯反演不容易懂。

至于如何求莫比乌斯函数：我们知道莫比乌斯函数跟欧拉函数一样都是积性函数，所以我们可以同 欧拉筛一样吧莫比乌斯函数筛出来。

void get_mu(ll n){
mu[1]=1;// 存放 莫比乌斯函数；
//isprime[] 存放 是否是质数
//prime[] 存放 质数
for(int i=2;i<=n;i++){
if(!isprime[i]) {
prime[++cnt]=i;
mu[i]=-1;
}
for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
isprime[i*prime[j]]=1;
if(i%prime[j]==0){mu[i*prime[j]]=0;break;}//也可以直接break 因为里面本来存的就是0
else mu[i*prime[j]]=-mu[i];
}
}
}

莫比乌斯反演

我只是掌握皮毛，有深层次的理解在更新，有更好的理解也可以分享给我哦~~~。 不胜感激！

莫比乌斯反演的引入：

若 .

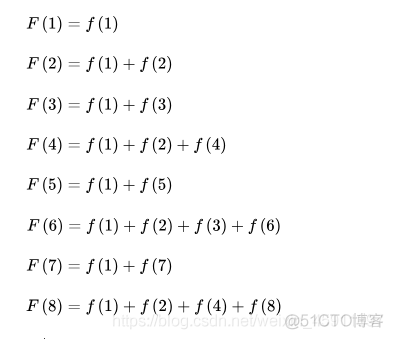
那么

从中，可以看出，若 n=p²(p是质数)那么,所以

通过推广我们可以得到就像n=8，(！=p²) 他也满足这个式子

根据上个推广的来的式子我们 就可以说 莫比乌斯反演定理了。

莫比乌斯反演定理

设 和是定义在正整数集合上的两个函数定义如下:

若函数函数:

则有：

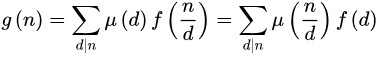
莫比乌斯反演定理证明

​​参考着个吧​​ 理解就行。重要是定理。(个人认为)

莫比乌斯反演另一性质(与欧拉函数有关)

若n>1且n为正整数，则有
若n=1，则该式为1、
2，
对任意正整数n均有：

【文章原创作者：cc防御 http://www.558idc.com/gfip.html提供，感恩】