前言:滑动窗口最大值问题是很经典的算法问题。本文描述了它的求解过程,分析了时间复杂度,证明了其正确性。
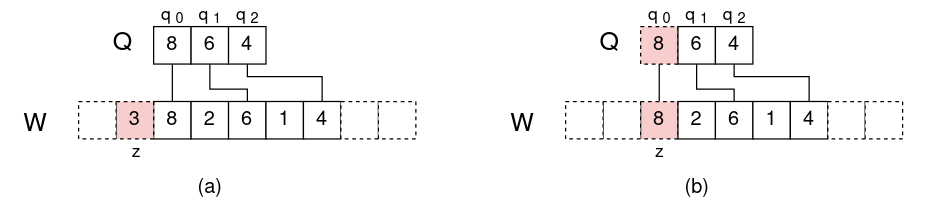
什么是滑动窗口最大值问题用一个长度固定的滑动窗口W在一个数组上逐元素滑动,求每次滑动后W内的最大元素。例如:长度为3的滑动窗口在数组[3,4,1,5,2]上滑动,在(a)和(b)两个时刻窗口内最大值分别为4和5。如下图所示:
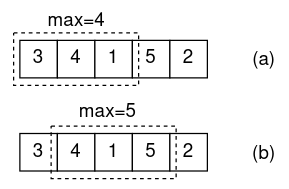
你可以在leetcode上找到相关题目。
最容易想到的方法就是遍历每一时刻下滑动窗口内的所有元素,找到其最大值。整个过程简单直观,无需证明。复杂度上,易得空间复杂度是O(1),时间复杂度是O(N*K),其中N是数组长度,K是滑动窗口大小。因为需要滑动N次,每次遍历K个元素。
高阶解法高阶解法在整个滑动过程中维护了一个队列Q。某时刻滑窗滑入的新元素记为x、滑出的旧元素记为z,则Q的更新步骤为:
- 更新步骤一: 从Q的尾部依次弹出所有小于x的元素,然后把x压入Q的队尾
- 更新步骤二: 如果Q的队首元素等于z,则Q弹出队首
执行以上操作后,Q的队首元素即为当前滑动窗口最大值。过程如图所示:
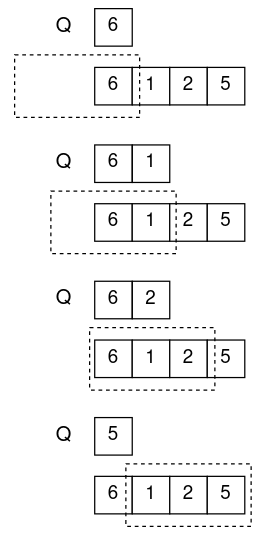
空间上,需要额外的空间存储Q,Q的最大长度不超过K,因此空间复杂度是O(K)。
时间上,共迭代了N次,每次需要对Q做压入和弹出操作。最差的情况,某次迭代会弹出Q所有元素。Q的长度最大为K,所以貌似时间代价是O(NK);但实际上,从整体看,所有的元素都会压入一次,弹出一次,所以实际复杂度其实为O(N)。
证明算法每次迭代都维持了一个条件不变式:
-
条件一:Q是W的子序列。
-
条件二:在W中,\(q_0\)是最大的元素,\(q_{i+1}\)是\(q_{i}\)之后最大的元素。数组下标从0开始。
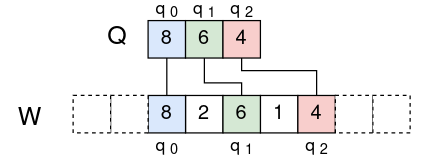
例如上图中,
- Q=(8,6,4)是W的子序列
- 在W中,8是W中最大的元素,6是8之后最大的元素,4是6之后最大的元素
值得注意的是,如果最大的元素存在多个,则认为是它们中的第一个。
过程分析按照上文的更新规则,更新过程可以表述为:
- 滑窗纳入新元素x,x挤掉Q尾部所有小于它的元素,然后追加到Q。
- 滑窗弹出旧元素z,如果Q首元素等于z,则从Q弹出首元素
我们先来关注过程一。过程一可能有几个情况:
Case 1: x挤掉了Q的所有元素,说明它大于Q中所有元素,此时Q中只剩下x,显然这时候满足条件二。
Case 2: x没有挤掉任何Q的元素,说明x小于等于Q的所有元素。此时x会追加到Q的尾部,显然这时候满足条件二。
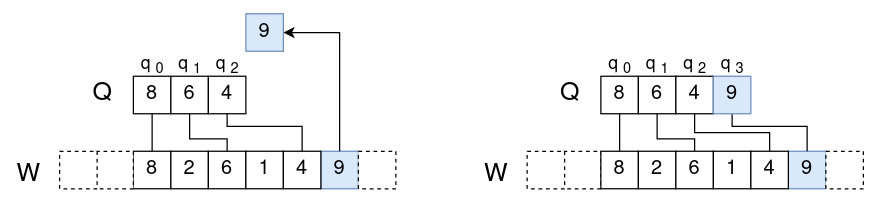
Case 3:x挤掉了Q的一部分元素,说明x大于Q尾部的一个或多个元素。
我们假设
\[q_k \ge x > \{ q_{k+1},...,q_m \} \]则x会挤掉原来的 \(\{ q_{k+1},...,q_m \}\) 成为新的\(q_{k+1}\)。
此时条件二成立:x比\(q_0\)小,不会动摇它的地位;x比\(q_{k+1}\)大,而后者是W中\(q_k\)之后最大的元素,因此x自然也是\(q_k\)之后最大的元素,那么x成为新的\(q_{k+1}\)后,自然满足条件二。
此时我们关注过程一。如果滑窗弹出的元素就是\(q_0\),那么Q自然也应该弹出\(q_0\),这样才能满足条件一。
-
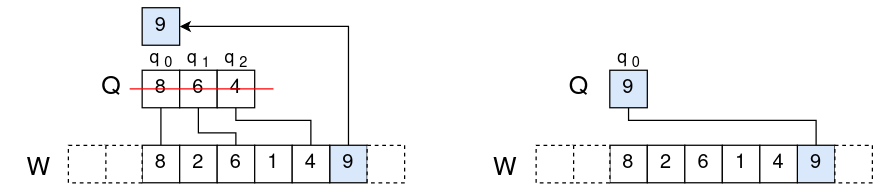
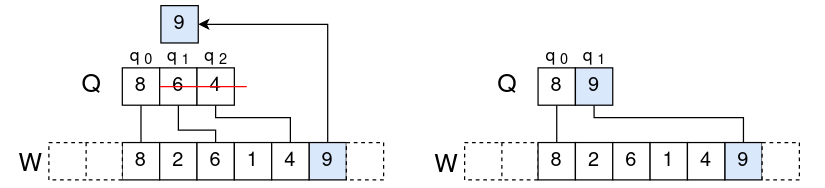
如果W弹出的元素z不等于\(q_0\),那么无需处理,如下图中情况(a)所示。
-
如果z等于\(q_0\),那么可以确定弹出的就是\(q_0\),毕竟\(q_0\)是W中的最大元素(如果最大元素有多个则为第一个)。此时W和Q都弹出\(q_0\)后,依然符合条件一和条件二,这里不再证明。情况如下图(b)所示。
至此,证明完毕。
我们可以简单理解一下:Q是W的子序列,当W失去元素z时,Q自然也要失去它;如果W新来了一个很大的元素x,那么直到它被弹出之前,在前面比它小的元素是没有出头之日的。在它弹出之后,它前面的元素自然也早被弹出了。所以在前面比它小的元素都没有用,可以即刻弹出。
