Python之数据分析（Numpy中的除法和取余、三角函数、ufunc对象的位运算）

文章目录

• ​​一、四种除法​​
• ​​二、取余运算​​
• ​​三、斐波那契数的四种求法​​
• ​​四、坐标变化的三角函数​​
• ​​五、ufunc对象位运算​​

一、四种除法

1、真除： 结果完全保留，小数部分也保留
1）numpy.true_divide()
2）numpy.divide()
3）也可以直接用‘/’除法运算符，结果也是真除结果

2、地板除： 将除法结果向下取整，往小的取整
1）numpy.floor_divide()
2）运算符号‘//’

3、天花板除： 将除法结果向上取整，往大的取整
没有具体函数，可以先做真除，再天花板取整(ceil)，再取int类型

4、截断除： 直接去除小数部分取整
没有具体函数，可以先做真除，再截断取整(trunc)，再取int类型

5、练习代码

import numpy as np

a = np.array([5, 5, -5, -5])
b = np.array([2, -2, 2, -2])
print(a, b)

# 真除
c1 = np.true_divide(a, b)
c2 = np.divide(a, b)
c3 = a / b
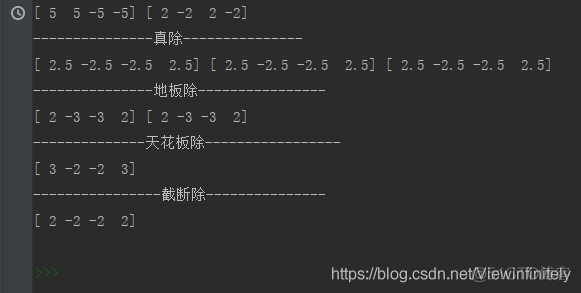
print("---------------真除---------------")
print(c1, c2, c3)

# 地板除
d1 = np.floor_divide(a, b)
d2 = a // b
print("---------------地板除----------------")
print(d1, d2)

# 天花板除
e = np.ceil(a/b).astype(int)
print("--------------天花板除-----------------")
print(e)

# 截断除
f = np.trunc(a/b).astype(int)
print("----------------截断除---------------")
print(f)

二、取余运算

1、地板余数： 做地板除之后得到的余数
1）numpy.remainder()
2）numpy.mod()
3）取余运算符号‘%’

2、截断余数： 做截断除之后得到的余数
numpy.fmod()

3、练习代码

import numpy as np

a = np.array([5, 5, -5, -5])
b = np.array([2, -2, 2, -2])
print(a, b)

# 地板取余
c1 = np.remainder(a, b)
c2 = np.mod(a, b)
c3 = a % b
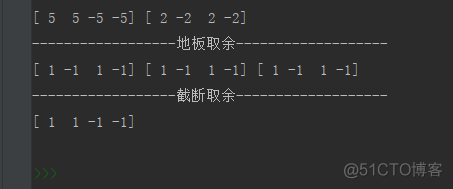
print("------------------地板取余-------------------")
print(c1, c2, c3)

# 截断取余
d = np.fmod(a, b)
print("------------------截断取余-------------------")
print(d)

三、斐波那契数的四种求法

1、递归方式

n = 30
def fibo(n):
return fibo(n-1) + fibo(n-2) if n>=3 else 1
print(fibo(n))

2、循环方式： 不需要占用太多内存，效率高于上一种

n = 30
f1, f2 = 0, 1 # 记录相加的两项
for i in range(n): # fn是从f0开始的，得到第一项是1，第二项也是1
fn = f1 + f2
# 加完之后就需要交换一下值
f1, f2 = fn, f1
print(fn)

3、矩阵方式： 效果更高

import numpy as np
n = 30
print(int((np.mat('1. 1.; 1. 0.') ** (n-1))[0, 0]))

4、根号方式

import numpy as np
n = 30
r = np.sqrt(5)
print(int((((1+r)/2) ** n - ((1-r)/2) ** n)/r))

四、坐标变化的三角函数

1、ufunc对象须知
python中几乎所有的算数和关系运算符都被numpy借助ufunc对象实现为可对数组操作的矢量化运算符

2、实现原理
numpy中的三角函数都是ufunc对象，可以对参数数组中的每个元素进行三角函数运算，并将运算结果以数组形式返回
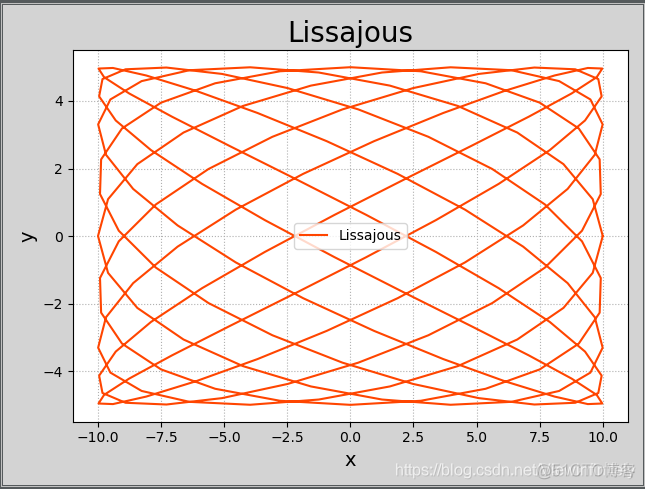
横纵坐标数据都随三角函数变化的曲线（如两个方向的交流电）：
x = Asin(at+pi/2)
y = Bsin(bt)

3、参考代码

import numpy as np
import matplotlib.pylab as mp

t = np.linspace(0, 2*np.pi, 201) # 用201个点来记录位置信息
# A, a, B, b = 10, 1, 5, 1
# A, a, B, b = 10, 1, 5, 2 # 频率改成2
A, a, B, b = 10, 9, 5, 7 # 频率改成非整数倍
x = A * np.sin(a*t + np.pi/2)
y = B * np.sin(b*t)

# 绘制曲线
mp.figure('Lissajous', facecolor='lightgray')
mp.title('Lissajous', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(x, y, c='orangered', label='Lissajous')
mp.legend()
mp.show()

五、ufunc对象位运算

1、异或运算： 只要是相同的就是0，不同的就是1。在numpy中，符号相同的是正数，符号不同的是负数。

• ^或__xor__或bitwise_xor
• 1^0=1
  1^1=0
  0^0=0
  0^1=1

2、位与运算： 只要有0就是0，在numpy中，只要两个不同，结果就是0，凡是2的次方的结果都是0

• &或__and__或bitwise_and
• 1&0=0
  0&0=0
  0&1=0
  1&1=1

3、移位运算： 左移相当于除2，右移相当于乘2

• 左移(除2)：<<或__lshift__或left_shift
• 右移(乘2)：>>或__rshift__或right_shift

4、练习代码