sg函数训练——开窍篇

个人觉得，能做一道经典的题并理解透彻，往往比做对难度系数很大的题目更有意义。最近又训练了博弈，记录一些题目，来个小总结。

hdu 3032 Nim or not Nim？

​​http://acm.hdu.edu.cn/showproblem.php?pid=3032​​​
大意：和普通的nim游戏相比，这里新添加了一种操作，可以把数字分成更小的两份。
分析：
sg[0]=0
当i=1，取走1后剩下0，mex[1]=1. sg[1]=1
当i=2时，可以取1，2，剩下1，0，sg[1]=1，sg[0]=0，分解成1+1，sg[1]^sg[1]=0，即分解相同的两部分和取走全部的效果是一样的。mex(2)=2 sg[2]=2
当i=3时，可以取1，2，3，剩下2，1，0，sg[2]=2, sg[1]=1, sg[0]=0，分解: sg[1]^sg[2]=3，所以mex(3)=4. sg[3]=4
当i=4时，取：1，2，3，4，剩下：sg[3]=4, sg[2]=2, sg[1]=1, sg[0]=0, 分解: sg[1]^sg[3]=5 mex(5)=3. sg[4]=3.

打表：

int sg[N];
bool vis[N];
void init(int n){
int i,j;
for(i=2;i<n;i++){
memset(vis,0,sizeof(vis));
for(j=1;j<=n;j++) vis[sg[i-j]]=1; // 取
for(j=1;j+j<=n;j++) vis[sg[j]^sg[i-j]]=1; // 分解
j=0;
while(vis[j]) j++;
sg[i]=j;
}
}
/*
1: 1
2: 2
3: 4
4: 3
5: 5
6: 6
7: 8
8: 7
9: 9
10: 10
11: 12
12: 11
13: 13
14: 14
15: 16
16: 15
17: 17
18: 18
19: 20
20: 19
21: 21
22: 22
23: 24
24: 23
*/

得到规律：
sg[4n+3]=4n+4
sg[4n]=4n-1
sg[i]=i

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

int main()
{
//freopen("cin.txt","r",stdin);
int n,t;
cin>>t;
while(t--){
scanf("%d",&n);
int a,ans=0;
for(int i=0;i<n;i++){
scanf("%d",&a);
if((a&3)==3) { // a%4==3
ans=ans^(a+1);
}
else if((a&3)==0){ // a%4==0
ans=ans^(a-1);
}
else ans=ans^a;
}
if(ans) puts("Alice");
else puts("Bob");
}
return 0;
}

acdream 1112 Alice and Bob

​​http://acdream.info/problem?pid=1112​​​
大意：给出一堆数字，每一个数字可以被不是它本身的约数（包括1）替代，或者分解成两个约数。比如6可以变成：2, 3, (2,3)
分析：一开始使用直接分解计算的方法果断超时。事实上这个问题完全可以从另一个角度看，由算术基本定理可知， n=ap11ap22⋯apkk 那么n变小的过程就是素因子减少的过程。由此问题变成n的素因子个数变少的sg问题。
对于范围是5e6的未知数，可以猜想他的素因子的个数一定小于30（1<<30一定大于它）
由此我们可以算出每一个数字的素因子的个数，然后计算出这30个数字的sg函数值（预处理）。
至于如何计算出每一个数字的素因子的个数，可以使用前缀和的思想，sum[n]=sum[n/p]+1 （假设p是n的最小素因子）

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N=5e6+10;
int sg[N],minp[N],sum[N];
int maxs,cnt;
vector<int> prim;
bool vis[N];
void get_minp(){
minp[0]=minp[1]=0;
for(int i=2;i<N;i++) minp[i]=i;
for(int i=2;i<N;i++){
if(!vis[i]){ prim.push_back(i); cnt++; }
for(int j=0;j<cnt && prim[j]*i<N;j++){
int t=i*prim[j];
vis[t]=1;
minp[t]=min(minp[t],prim[j]);
if(i%prim[j]==0) break;
}
}
}
void get_sg(){
sg[0]=0;
sum[0]=sum[1]=0;
maxs=0;
int i,j;
for(i=2;i<N;i++){
sum[i]=sum[i/minp[i]]+1;
maxs=max(maxs,sum[i]);
}
for(i=1;i<=maxs;i++){
for(j=0;j<=i+1;j++) vis[j]=0; // important!!!
for(j=1;j+j<=i;j++){
int t1=sg[j], t2=sg[i-j];
vis[t1]=vis[t2]=vis[t1^t2]=1;
}
vis[0]=1; // 用1代替原数字
j=0;
while(vis[j]) j++;
sg[i]=j;
}
}
int main()
{
//freopen("cin.txt","r",stdin);
get_minp();
get_sg();
int n,a;
while(~scanf("%d",&n)){
int ans=0;
for(int i=0;i<n;i++){
scanf("%d",&a);
ans=ans^sg[sum[a]];
}
if(ans) puts("Alice");
else puts("Bob");
}
return 0;
}

Treblecross

此题类似于： uva 10561

​​https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1502​​

大意：对一个一维的棋带，两人玩游戏，每一个人将其中的 ‘.’ 变成 ‘x’ ,谁最先满足走一步棋后又3个连续的x排列在一起谁就胜利。

分析：《算法竞赛 训练指南》 p139

对于：_ _ x的情况再走一步棋必败，所以得到 _ _ x _ _ 的影响领域，

进一步分析：

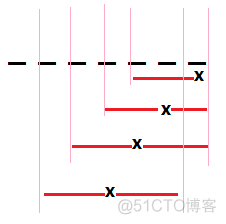
一个x的影响：sg(x)=mex(sg(x-3), sg(x-4), sg(x-5), sg(1)^sg(x-6), sg(2)^(sg(x-7)……)

所以枚举每一个点，然后计算sg异或结果，得到能够放棋子的位置

初始值：

sg(0)=0

sg(1)=sg(2)=sg(3)=1

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=210,inf=0x3f3f3f3f;
char str[N];
int sg[N];
int mex(int n){ // 递归求解sg[n]
if(sg[n]!=-1) return sg[n];
if(n==0) return sg[0]=0;
bool tag[N];
memset(tag,0,sizeof(tag));
/*for(int i=3;i<6&&i<=n;i++) tag[mex(n-i)]=1;
for(int i=6;i<=n;i++){
int g=mex(n-i)^mex(i-5);
tag[g]=1;
}*/
for(int i=1;i<=n;i++){
int g=mex(max(0,i-3))^mex(max(0,n-i-2));
tag[g]=1;
}
for(int i=0;i<N;i++)
if(tag[i]==0) return sg[n]=i;
}
bool win(int n,int dex){ // 检测 XXX 区域
char ch=str[dex];
str[dex]='X';
for(int i=0;i+2<n;i++){
if(str[i]=='X' && str[i+1]=='X' && str[i+2]=='X') {
str[dex]=ch;
return true;
}
}
str[dex]=ch;
return false;
}
bool will_win(int n,int dex){ // 检测 . 区域
char ch=str[dex];
str[dex]='X';
for(int i=0;i<N;i++){ // 第二种情况里的假设可能造成第一种情况成立，
if(str[i]=='.'){ //但它不属于第二种情况
if(win(n,i)) {
str[dex]=ch;
return false;
}
}
}

int ans=0,temp=0;
for(int i=0;i<n;i++){
if(str[i]=='X' || (i-1>=0&&str[i-1]=='X') || (i-2>=0&&str[i-2]=='X')
|| (i+1<n&&str[i+1]=='X') || (i+2<n&&str[i+2]=='X')){
ans=ans^mex(temp);
temp=0;
}
else temp++;
}
ans=ans^mex(temp);
str[dex]=ch;
return ans==0;
}
int main()
{
//freopen("cin.txt","r",stdin);
memset(sg,-1,sizeof(sg));
//sg[0]=0;
//sg[1]=sg[2]=sg[3]=1;
int t,ca=1;
cin>>t;
while(t--){
scanf("%s",str);
int n=strlen(str);
int ans[N],top=0;
for(int i=0;i<n;i++){
if(str[i]=='X') continue;
if(win(n,i) || will_win(n,i)) ans[top++]=i+1;
}
if(top) {
printf("Case %d: ",ca++);
for(int i=0;i<top-1;i++) printf("%d ",ans[i]);
printf("%d\n",ans[top-1]);
}
else printf("Case %d: 0\n",ca++);
}
return 0;
}