A. NP-Hard Problem
time limit per test 2 seconds
memory limit per test 256 megabytes
input standard input
output standard output
Recently, Pari and Arya did some research about NP-Hard problems and they found the minimum vertex cover
Suppose the graph G is given. Subset A of its vertices is called a vertex cover of this graph, if for each edge uv there is at least one endpoint of it in this set, i.e.
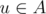
or
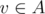
(or both).
Pari and Arya have won a great undirected graph as an award in a team contest. Now they have to split it in two parts, but both of them want their parts of the graph to be a vertex cover.
They have agreed to give you their graph and you need to find two disjoint subsets of its vertices A and B, such that both A and B
Input
The first line of the input contains two integers n and m (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of vertices and the number of edges in the prize graph, respectively.
Each of the next m lines contains a pair of integers ui and vi (1 ≤ ui, vi ≤ n), denoting an undirected edge between ui and vi. It's guaranteed the graph won't contain any self-loops or multiple edges.
Output
If it's impossible to split the graph between Pari and Arya as they expect, print "-1" (without quotes).
If there are two disjoint sets of vertices, such that both sets are vertex cover, print their descriptions. Each description must contain two lines. The first line contains a single integer k denoting the number of vertices in that vertex cover, and the second line contains kintegers — the indices of vertices. Note that because of m ≥ 1, vertex cover cannot be empty.
Examples
input
1 2
2 3
output
2
2
1 3
input
1 2
2 3
1 3
output
Note
In the first sample, you can give the vertex number 2 to Arya and vertices numbered 1 and 3 to Pari and keep vertex number 4
In the second sample, there is no way to satisfy both Pari and Arya.
题解:多校结束了,写道题压压惊。。。给你一些顶点和边,将顶点分为两组,同一组的任意两个顶点不能相连。输出两组的各点,若不能分,输出-1。
代码:
#include<bits/stdc++.h>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<map>
#include<cmath>
#include<queue>
#include<set>
#include<stack>
#include <utility>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define mst(a) memset(a, 0, sizeof(a))
#define M_P(x,y) make_pair(x,y)
#define pii pair<int,int>
#define rep(i,j,k) for (int i = j; i <= k; i++)
#define per(i,j,k) for (int i = j; i >= k; i--)
#define lson x << 1, l, mid
#define rson x << 1 | 1, mid + 1, r
const int lowbit(int x) { return x&-x; }
const double eps = 1e-8;
const int INF = 1e9+7;
const ll inf =(1LL<<62) ;
const int MOD = 1e9 + 7;
const ll mod = (1LL<<32);
const int N = 2e5+10;
const int M=100010;
template <class T1, class T2>inline void getmax(T1 &a, T2 b) {if (b>a)a = b;}
template <class T1, class T2>inline void getmin(T1 &a, T2 b) {if (b<a)a = b;}
int read()
{
int v = 0, f = 1;
char c =getchar();
while( c < 48 || 57 < c ){
if(c=='-') f = -1;
c = getchar();
}
while(48 <= c && c <= 57)
v = v*10+c-48, c = getchar();
return v*f;
}
vector<int>G[100010];
vector<int>ans[2];
int vis[100010];
int ok;
int type[100010];
void dfs(int u,int fa,int ty) //u的父亲是fa
{
ans[ty].push_back(u); //存储二分图
vis[u]=1;
type[u]=ty;
int d=G[u].size(); //结点u的相邻点个数
for(int i = 0;i< d ;i++)
{
int v = G[u][i]; //结点u的第i个相邻点v
if(v==fa)
continue;
if(vis[v]&&type[v]==type[u])
ok=1;
if(vis[v])
continue;
dfs(v,u,1-ty); //把 v 的父亲设为 u,继续递归
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
#endif
int n,m;
ok = 0;
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
G[u].push_back(v);
G[v].push_back(u);
}
for(int i = 1;i <= n; i++)
if(!vis[i]&&!ok)
dfs(i,-1,0);
if(ok)
{
puts("-1");
return 0;
}
printf("%d\n",ans[0].size());
for(int i=0;i<ans[0].size()-1;i++)
printf("%d ",ans[0][i]);
printf("%d\n",ans[0][ans[0].size()-1]);
printf("%d\n",ans[1].size());
for(int i=0;i<ans[1].size()-1; i++)
printf("%d ",ans[1][i]);
printf("%d\n",ans[1][ans[1].size()-1]);
return 0;
}
