1 内容介绍
小波变换在信号的滤波降噪处理中应用非常广泛,针对传统小波阈值去噪算法中软,硬阈值函数以及Garrote阈值函数的不足,构造出一个新的阈值函数,并采用新的阈值确定方法,对信号的去噪处理更加灵活,克服了传统阈值函数的不足.通过Matlab软件,对传统阈值函数以及本文提出的改进阈值函数进行去噪处理仿真,在信噪比(SNR)和均方误差(MSE)两个方面进行定量对比.实验结果表明,使用改进的阈值函数进行去噪处理后,信号具有更高的信噪比和更小的均方误差,去噪效果优于传统方法.


2 仿真代码
clear all;
close all
[x,Fs]=audioread('d00.wav');
t=(0:length(x)-1)/Fs; %计算样本时刻
noise=0.2*rand(length(x),1);
noise1 = wgn(length(x),1,-30);
x0=x; %原始信号
x=x+noise1;
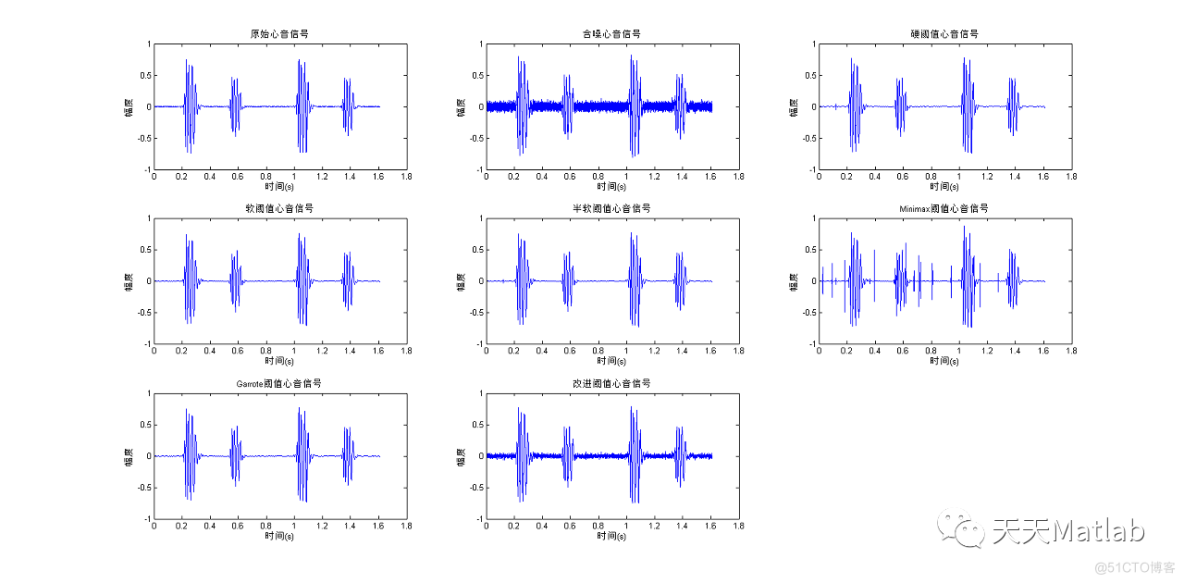
subplot(331); plot(t,x0); ylabel('幅度'); xlabel('时间(s)'); title('原始心音信号');
subplot(332); plot(t,x); ylabel('幅度'); xlabel('时间(s)'); title('含噪心音信号');
ylim([-1 1]);
[xd1,xd2,xd3,xd4,xd5,xd6]=softthersh(x,6,'db6');
subplot(333); plot(t,xd1); ylabel('幅度'); xlabel('时间(s)'); title('硬阈值心音信号');
subplot(334); plot(t,xd2); ylabel('幅度'); xlabel('时间(s)'); title('软阈值心音信号');
subplot(335); plot(t,xd3); ylabel('幅度'); xlabel('时间(s)'); title('半软阈值心音信号');
subplot(336); plot(t,xd4); ylabel('幅度'); xlabel('时间(s)'); title('Minimax阈值心音信号');
subplot(337); plot(t,xd5); ylabel('幅度'); xlabel('时间(s)'); title('Garrote阈值心音信号');
subplot(338); plot(t,xd6); ylabel('幅度'); xlabel('时间(s)'); title('改进阈值心音信号');
% subplot(339); plot(t,xd7); ylabel('幅度'); xlabel('时间(s)'); title('新改进阈值心音信号');
[SNR1,RMSE1]=Evaluate(x0,xd1);
[SNR2,RMSE2]=Evaluate(x0,xd2);
[SNR3,RMSE3]=Evaluate(x0,xd3);
[SNR4,RMSE4]=Evaluate(x0,xd4);
[SNR5,RMSE5]=Evaluate(x0,xd5);
[SNR6,RMSE6]=Evaluate(x0,xd6);
% [SNR7,RMSE7]=Evaluate(x0,xd7);
3 运行结果
4 参考文献
[1]袁孟宇. 基于改进小波阈值法的动液面信号去噪研究[D]. 东北石油大学.
[2]刘佳林, 孙旋. 基于改进阈值函数小波语音增强方法的研究[J]. 软件导刊, 2010(2):3.
