1 内容介绍
随着国民经济的持续快速发展,全社会对电力的需求显著增加,为了缓和全社会用电紧张局面,电力工业得到了迅速的发展,但是却造成了能源浪费和过量污染物排放,为此国家要求按照发电机组的类型以及能源消耗进行发电排序.我国目前电力结 构以火电为主,并且由于电网安全稳定约束条件的限制,不能仅仅以发电序位表为标准,按照机组煤耗率从小到大依次满发,必须在考虑电网安全稳定运行的基础上,对火电机组进行机组组合,因此,机组组合将成为我国现阶段节能发电调度工作的核心.机组组合问题是一个高维,离散,非线性的优化问题,很难找出理论上的最优解,但由于其所带来的显著效益,人们一直在积极的研究,提出各种方法来解决这个问题. 本文首先按照节能发电调度的要求,以节约能耗,降低排污为目标,建立了节能发电调度机组组合问题的数学模型,并在目标函数中考虑了由于潮流分布变化而引起的网损的变化.对于模型的约束条件考虑了机组出力限制约束,节点电压约束,线路潮流约束,机组爬坡速率约束等条件. 对于机组组合优化问题的求解。
2 仿真代码
%********************************************************************
%主函数,用粒子群算法,求6台机组发电调度成本目标函数最低
%Script file for the initialization and run of the differential
% evolution optimizer.
%********************************************************************
clc;
clear;
close all;
%参数设置:第1行是上网电价,第2行是最小发电量,第3行是最大发电量
SI.gp=[ 415 418 420 422 430 428;
30 30 100 100 250 300;
350 400 600 650 800 1000];
%网损系数(Bij为电厂i和电厂j之间的网损系数)
SI.lc=[0.002022 -0.000286 -0.000534 -0.000565 -0.000454 0.000103;
-0.000286 0.003243 0.000016 -0.000307 -0.000422 -0.000147;
-0.000534 0.000016 0.001085 0.000831 0.000023 -0.000270;
-0.000565 -0.000307 0.000831 0.001129 0.000113 -0.000295;
-0.000454 -0.000422 0.000023 0.000113 0.000460 -0.000153;
0.000103 -0.000147 -0.000270 -0.000295 -0.000153 0.000898;
];
SI.TG=2400;%电量需求(MWh)
for i=1:I_itermax
%粒子群算法
w=ws-(ws-we)*(i/I_itermax)^2;
for j=1:I_NP
V(j,:) = w*V(j,:) + c1*rand*(Gbest_pop (j,:) - pop(j,:)) + c2*rand*(Zbest_pop - pop(j,:));
for k=1:I_D %----boundary constraints via bounce back-------
if (V(j,k) > Vmax(k))
V(j,k) = Vmax(k);
end
if (V(j,k) <Vmin(k))
V(j,k) =Vmin(k);
end
end
pop(j,:)=pop(j,:)+V(j,:);
%-----Select which vectors are allowed to enter the new population------------
for k=1:I_D %----boundary constraints via bounce back-------
if (pop(j,k) > FVr_maxbound(k))
pop(j,k) = FVr_maxbound(k)+rand*(Zbest_pop(k) - FVr_maxbound(k));
end
if (pop(j,k) < FVr_minbound(k))
pop(j,k) = FVr_minbound(k)+rand*(Zbest_pop(k) - FVr_minbound(k));
end
end
% pop(j, (pop(j,:)<SI.gp(2,:)))= SI.gp(2, (pop(j,:)<SI.gp(2,:)));
% pop(j, (pop(j,:)>SI.gp(3,:)))= SI.gp(2, (pop(j,:)>SI.gp(3,:)));
chromosome(j,:)= objfun(pop(j,:),SI);
if(chromosome(j,I_D+M)<Gbest(j))
Gbest(j)=chromosome(j,I_D+M);
Gbest_pop(j,:)=chromosome(j,1:I_D);
end
if(chromosome(j,I_D+M)<Zbest)
Zbest=chromosome(j,I_D+M);
Zbest_pop=chromosome(j,1:I_D);
end
end
Zbestit(i+1) =Zbest;
Zbestit_pop(i+1,:)=Zbest_pop;
if ~mod(i,I_refresh) %如果i除以S_struct.I_refresh的余数为0,输出i。
fprintf('%d\n',i);
end
end
toc
P_Sum=0;P_loss=0;
P_Sum=sum(Zbest_pop);
P_loss=Zbest_pop*SI.lc*Zbest_pop';
disp(['最优解——> 出力 : ',num2str(Zbest_pop),' 成本:',num2str(Zbest)]);
disp(['出力总和(MW):',num2str(P_Sum),' 网损(MW):',num2str(P_loss)])
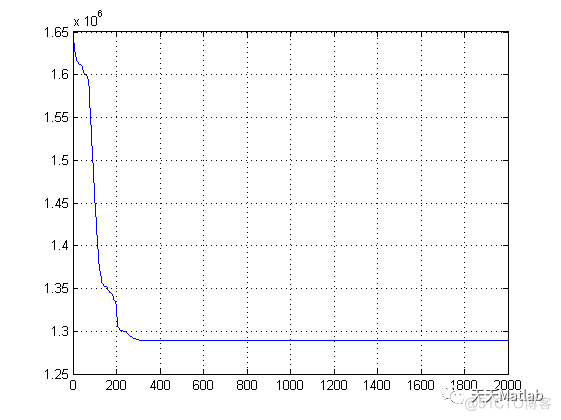
figure
title('Best cost');
plot( Zbestit);
xlim([0 I_itermax]);
grid on;
hold off
3 运行结果
最优解——> 出力 : 350 322.3344 309.2298 471.2568 800 785.2812 成本:1288833.0546
出力总和(MW):3038.1023 网损(MW):638.1023
4 参考文献
[1]程宇旭. 基于改进粒子群算法的微电网能量优化调度研究及实现[D]. 中南大学, 2014.
