漏了个阶梯博弈没学,前来补补。。
阶梯博弈给出的问题如下:
从第0个阶梯起,每个阶梯上都有若干个石子,每次都可以从任一阶梯上取任意正整数个石子往下一个阶梯放,不能操作的人输
结论是:该状态的sg值为奇数阶梯上的石子的异或和
证明:
先证明这个模型可以转化为把奇数阶看成若干堆石子的nim博弈
如果对手从偶数阶往奇数阶放,那么我们可以从该奇数阶取相同的石子到下一阶,即将偶数阶的石子放到了下一个偶数阶,此时奇数阶的状态数不变
如果对手从奇数阶往偶数阶放,相当于把奇数阶上的石子拿掉了,此时可以根据nim博弈取相应的石子到达sg=0的状态
于是这个阶梯博弈就看成了奇数阶上的nim博弈,其sg值自然也是奇数阶上的石子数的异或和
再来看这个题。。我们需要将空隙看成石子,那么移动硬币相当于把空隙往右边放,相当于阶梯博弈中的把石子往下一个阶梯放,于是做个差分求个sg就可以了。。
注意排序TAT
这个其实还有另一种理解方法,就是将硬币22配对(若为奇数个硬币第一个硬币和左边界配对),那么配对出来的石子数其实就是空隙,如果移动左边的硬币,那么我们将右边的硬币移动相同的步数,石子数不变。如果移动了右边的硬币,那么相当于减少了石子数,那么此时可以根据nim的方法去调节sg值,然后把必败状态留给对手
/**
* ┏┓ ┏┓
* ┏┛┗━━━━━━━┛┗━━━┓
* ┃ ┃
* ┃ ━ ┃
* ┃ > < ┃
* ┃ ┃
* ┃... ⌒ ... ┃
* ┃ ┃
* ┗━┓ ┏━┛
* ┃ ┃ Code is far away from bug with the animal protecting
* ┃ ┃ 神兽保佑,代码无bug
* ┃ ┃
* ┃ ┃
* ┃ ┃
* ┃ ┃
* ┃ ┗━━━┓
* ┃ ┣┓
* ┃ ┏┛
* ┗┓┓┏━┳┓┏┛
* ┃┫┫ ┃┫┫
* ┗┻┛ ┗┻┛
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<stdlib.h>
#include<assert.h>
#define inc(i,l,r) for(int i=l;i<=r;i++)
#define dec(i,l,r) for(int i=l;i>=r;i--)
#define link(x) for(edge *j=h[x];j;j=j->next)
#define mem(a) memset(a,0,sizeof(a))
#define ll long long
#define eps 1e-8
#define succ(x) (1<<x)
#define lowbit(x) (x&(-x))
#define sqr(x) ((x)*(x))
#define mid (x+y)/2
#define NM 1005
#define nm 40005
#define pi 3.1415926535897931
const ll inf=1e9+7;
using namespace std;
ll read(){
ll x=0,f=1;char ch=getchar() ;
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[NM],n,s;
int main(){
int _=read();while(_--){
n=read();mem(a);s=0;
inc(i,1,n)a[i]=read();
sort(a+1,a+1+n);
dec(i,n,1)a[i]-=a[i-1],a[i]--;
reverse(a+1,a+1+n);
inc(i,1,n)if(i&1)s^=a[i];
puts(s?"Georgia will win":"Bob will win");
}
return 0;
}
Georgia and Bob
Description
Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example:
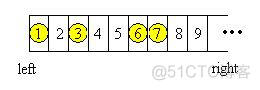
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.
Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.
Given the initial positions of the n chessmen, can you predict who will finally win the game?
Input
The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.
Output
For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.
Sample Input
23
1 2 3
8
1 5 6 7 9 12 14 17
Sample Output
Bob will winGeorgia will win
Source
POJ Monthly--2004.07.18
Time Limit: 1000MS
Memory Limit: 10000K
Total Submissions: 12678
Accepted: 4251
[Submit] [Go Back] [Status] [Discuss]

