1 内容介绍
SCE(shuffled complex evolution )是一种相对较新的连续性问题的元启发搜索算法。非常适合于求解具有多个局部最小的全局优化问题。SCE算法的主要特征是通过竞争进化和定期洗牌来确保每个复形获得的信息能在整个问题空间获得共享
2 部分代码
%% Solving Bin Packing Problem (BPP) by Shuffled Complex Evolution (SCE) Algorithm
% There are items with different sizes and bins with a constant size.
% Items should be placed inside bins with less bins used.
% Here 15 items with [6 3 4 6 8 7 4 7 7 5 6 9 4 2 3] values and bin size of 20 are used.
% Less bins, the better. You can change input data by 'CreateModel.m' file.
clc;
clear;
close all;
%% Problem Definition
model = CreateModel(); % Create Bin Packing Model
CostFunction = @(x) BinPackingCost(x, model); % Objective Function
nVar = 2*model.n-1; % Number of Decision Variables
VarSize = [1 nVar]; % Decision Variables Matrix Size
VarMin = 0; % Lower Bound of Decision Variables
VarMax = 1; % Upper Bound of Decision Variables
%% SCE-UA Parameters
MaxIt = 150; % Maximum Number of Iterations
nPopComplex = 5; % Complex Size
nPopComplex = max(nPopComplex, nVar+1); % Nelder-Mead Standard
nComplex = 2; % Number of Complexes
nPop = nComplex*nPopComplex; % Population Size
I = reshape(1:nPop, nComplex, []);
% CCE Parameters
cce_params.q = max(round(0.5*nPopComplex), 2); % Number of Parents
cce_params.alpha = 3; % Number of Offsprings
cce_params.beta = 5; % Maximum Number of Iterations
cce_params.CostFunction = CostFunction;
cce_params.VarMin = VarMin;
cce_params.VarMax = VarMax;
%% Initialization
% Empty Individual Template
empty_individual.Position = [];
empty_individual.Cost = [];
empty_individual.Sol = [];
% Initialize Population Array
pop = repmat(empty_individual, nPop, 1);
% Initialize Population Members
for i = 1:nPop
pop(i).Position = unifrnd(VarMin, VarMax, VarSize);
[pop(i).Cost pop(i).Sol] = CostFunction(pop(i).Position);
end
% Sort Population
pop = SortPopulation(pop);
% Update Best Solution Ever Found
BestSol = pop(1);
% Initialize Best Costs Record Array
BestCosts = nan(MaxIt, 1);
%% SCE-UA Main Loop
for it = 1:MaxIt
% Initialize Complexes Array
Complex = cell(nComplex, 1);
% Form Complexes and Run CCE
for j = 1:nComplex
% Complex Formation
Complex{j} = pop(I(j, :));
% Run CCE
Complex{j} = RunCCE(Complex{j}, cce_params);
% Insert Updated Complex into Population
pop(I(j, :)) = Complex{j};
end
% Sort Population
pop = SortPopulation(pop);
% Update Best Solution Ever Found
BestSol = pop(1);
% Store Best Cost Ever Found
BestCosts(it) = BestSol.Cost;
% Show Iteration Information
disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCosts(it))]);
end
%% Results
figure;
plot(BestCosts,'k', 'LineWidth', 2);
xlabel('ITR');
ylabel('Cost Value');
ax = gca;
ax.FontSize = 14;
ax.FontWeight='bold';
set(gca,'Color','c')
grid on;
%%
items=model.v;
itemindex=BestSol.Sol.B;
sizebins=size(itemindex);
for i=1: sizebins(1,1)
itemvalue{i}=items(itemindex{i});
end;
itemvalue=itemvalue';
%
disp(['Number of Items is ' num2str(model.n)]);
disp(['Items are ' num2str(items)]);
disp(['Bins size is ' num2str(model.Vmax)]);
disp(['Selected bins is ' num2str(BestCosts(end))]);
disp(['Selected bins indexes are ']);
itemindex
disp(['Selected bins values are ']);
itemvalue
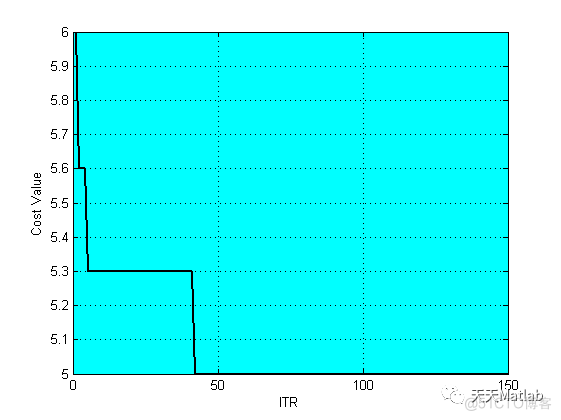
3 运行结果
4 参考文献
[1]张建林. Shuffled Complex Evolution算法及其在车间调度中的应用研究[D]. 兰州理工大学, 2013.
