
AI有道
不可错过的AI技术公众号
关注

重要通知
本公众号原名“红色石头的机器学习之路”已经改名为“AI有道”,请大家留意并继续关注本公众号!谢谢!
上节课我们主要介绍了如何建立一个实用的深度学习神经网络。包括Train/Dev/Test sets的比例选择,Bias和Variance的概念和区别:Bias对应欠拟合,Variance对应过拟合。接着,我们介绍了防止过拟合的两种方法:L2 regularization和Dropout。然后,介绍了如何进行规范化输入,以加快梯度下降速度和精度。然后,我们介绍了梯度消失和梯度爆炸的概念和危害,并提出了如何使用梯度初始化来降低这种风险。最后,我们介绍了梯度检查,来验证梯度下降算法是否正确。
本节课,我们将继续讨论深度神经网络中的一些优化算法,通过使用这些技巧和方法来提高神经网络的训练速度和精度。
——前言

1
Mini-batch Gradient Descent
之前我们介绍的神经网络训练过程是对所有m个样本,称为batch,通过向量化计算方式,同时进行的。如果m很大,例如达到百万数量级,训练速度往往会很慢,因为每次迭代都要对所有样本进行进行求和运算和矩阵运算。我们将这种梯度下降算法称为Batch Gradient Descent。
为了解决这一问题,我们可以把m个训练样本分成若干个子集,称为mini-batches,这样每个子集包含的数据量就小了,例如只有1000,然后每次在单一子集上进行神经网络训练,速度就会大大提高。这种梯度下降算法叫做Mini-batch Gradient Descent。

这里顺便总结一下我们遇到的神经网络中几类字母的上标含义:

Mini-batches Gradient Descent的实现过程是先将总的训练样本分成T个子集(mini-batches),然后对每个mini-batch进行神经网络训练,包括Forward Propagation,Compute Cost Function,Backward Propagation,循环至T个mini-batch都训练完毕。
Forward Propagation
ComputeCostFunction
BackwardPropagation
W:=W−α⋅dW
b:=b−α⋅db
}
经过T次循环之后,所有m个训练样本都进行了梯度下降计算。这个过程,我们称之为经历了一个epoch。对于Batch Gradient Descent而言,一个epoch只进行一次梯度下降算法;而Mini-Batches Gradient Descent,一个epoch会进行T次梯度下降算法。
值得一提的是,对于Mini-Batches Gradient Descent,可以进行多次epoch训练。而且,每次epoch,最好是将总体训练数据重新打乱、重新分成T组mini-batches,这样有利于训练出最佳的神经网络模型。
2
Understanding Mini-batch Gradient Descent
Batch gradient descent和Mini-batch gradient descent的cost曲线如下图所示:
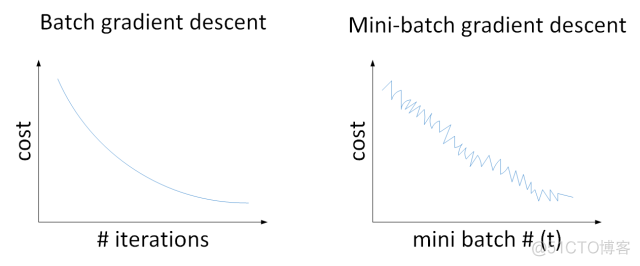
对于一般的神经网络模型,使用Batch gradient descent,随着迭代次数增加,cost是不断减小的。然而,使用Mini-batch gradient descent,随着在不同的mini-batch上迭代训练,其cost不是单调下降,而是受类似noise的影响,出现振荡。但整体的趋势是下降的,最终也能得到较低的cost值。


我们来比较一下Batch gradient descent和Stachastic gradient descent的梯度下降曲线。如下图所示,蓝色的线代表Batch gradient descent,紫色的线代表Stachastic gradient descent。Batch gradient descent会比较平稳地接近全局最小值,但是因为使用了所有m个样本,每次前进的速度有些慢。Stachastic gradient descent每次前进速度很快,但是路线曲折,有较大的振荡,最终会在最小值附近来回波动,难以真正达到最小值处。而且在数值处理上就不能使用向量化的方法来提高运算速度。
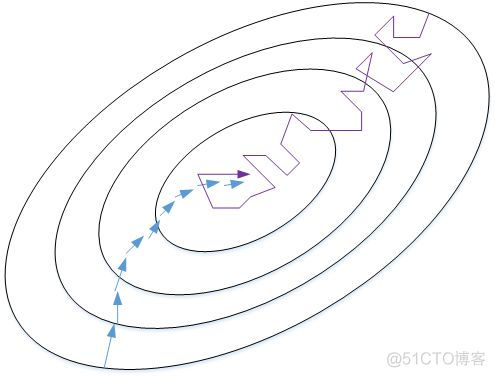
实际使用中,mini-batch size不能设置得太大(Batch gradient descent),也不能设置得太小(Stachastic gradient descent)。这样,相当于结合了Batch gradient descent和Stachastic gradient descent各自的优点,既能使用向量化优化算法,又能叫快速地找到最小值。mini-batch gradient descent的梯度下降曲线如下图绿色所示,每次前进速度较快,且振荡较小,基本能接近全局最小值。
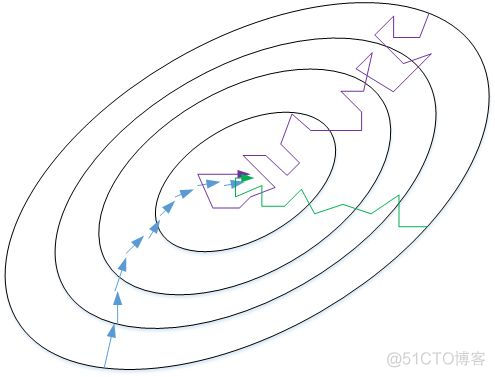
一般来说,如果总体样本数量m不太大时,例如m≤2000m≤2000,建议直接使用Batch gradient descent。如果总体样本数量m很大时,建议将样本分成许多mini-batches。推荐常用的mini-batch size为64,128,256,512。这些都是2的幂。之所以这样设置的原因是计算机存储数据一般是2的幂,这样设置可以提高运算速度。
3
Exponentially Weighted Averages
该部分我们将介绍指数加权平均(Exponentially weighted averages)的概念。
举个例子,记录半年内伦敦市的气温变化,并在二维平面上绘制出来,如下图所示:
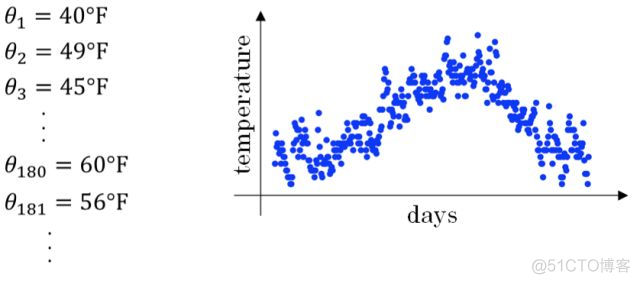
看上去,温度数据似乎有noise,而且抖动较大。如果我们希望看到半年内气温的整体变化趋势,可以通过移动平均(moving average)的方法来对每天气温进行平滑处理。
例如我们可以设V0=0,当成第0天的气温值。
第一天的气温与第0天的气温有关:
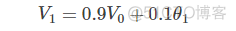
第二天的气温与第一天的气温有关:
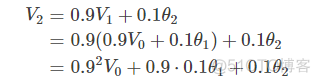
第三天的气温与第二天的气温有关:
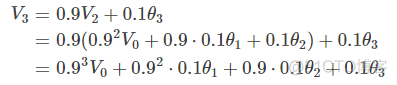
即第t天与第t-1天的气温迭代关系为:
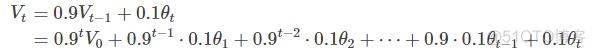
经过移动平均处理得到的气温如下图红色曲线所示:
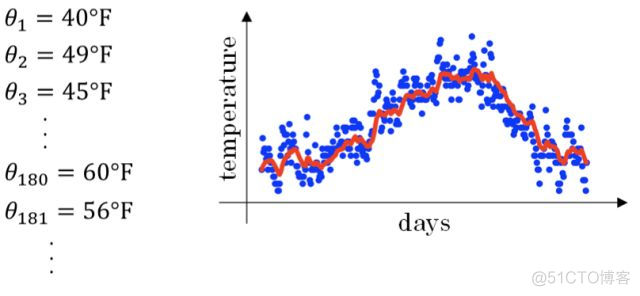
这种滑动平均算法称为指数加权平均(exponentially weighted average)。根据之前的推导公式,其一般形式为:
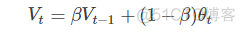
上面的例子中,β=0.9。ββ值决定了指数加权平均的天数,近似表示为:
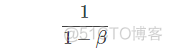

这里简单解释一下公式1/(1−β)是怎么来的。准确来说,指数加权平均算法跟之前所有天的数值都有关系,根据之前的推导公式就能看出。但是指数是衰减的,一般认为衰减到1/e就可以忽略不计了。因此,根据之前的推导公式,我们只要证明:
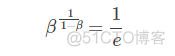
就好了。

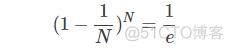
显然,当N>>0时,上述等式是近似成立的。
至此,简单解释了为什么指数加权平均的天数的计算公式为1/(1−β)。
4
Understanding Exponetially Weighted Averages
我们将指数加权平均公式的一般形式写下来:
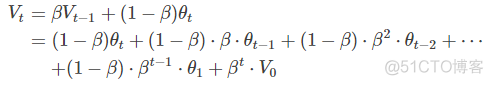

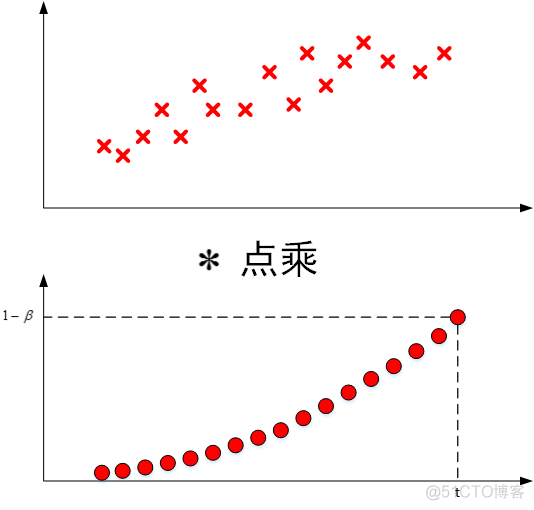
我们已经知道了指数加权平均的递推公式。实际应用中,为了减少内存的使用,我们可以使用这样的语句来实现指数加权平均算法:
Vθ=0
Repeat {
Get next θt
Vθ:=βVθ+(1−β)θt
}
5
Bias Correction in Exponentially Weighted Average
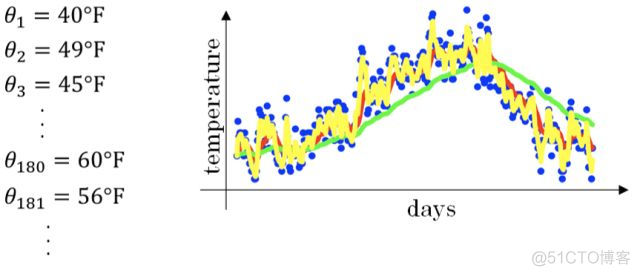
上文中提到当β=0.98时,指数加权平均结果如下图绿色曲线所示。但是实际上,真实曲线如紫色曲线所示。
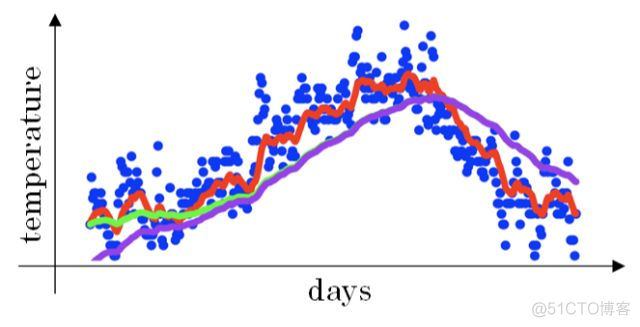
我们注意到,紫色曲线与绿色曲线的区别是,紫色曲线开始的时候相对较低一些。这是因为开始时我们设置V0=0,所以初始值会相对小一些,直到后面受前面的影响渐渐变小,趋于正常。
修正这种问题的方法是进行偏移校正(bias correction),即在每次计算完Vt后,对Vt进行下式处理:
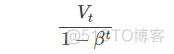

值得一提的是,机器学习中,偏移校正并不是必须的。因为,在迭代一次次数后(t较大),Vt受初始值影响微乎其微,紫色曲线与绿色曲线基本重合。所以,一般可以忽略初始迭代过程,等到一定迭代之后再取值,这样就不需要进行偏移校正了。
6
Gradient Descent with Momentum
该部分将介绍动量梯度下降算法,其速度要比传统的梯度下降算法快很多。做法是在每次训练时,对梯度进行指数加权平均处理,然后用得到的梯度值更新权重W和常数项b。下面介绍具体的实现过程。
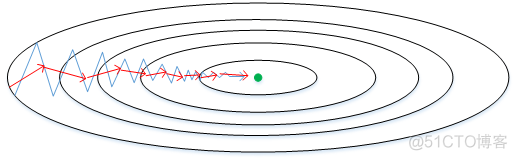
原始的梯度下降算法如上图蓝色折线所示。在梯度下降过程中,梯度下降的振荡较大,尤其对于W、b之间数值范围差别较大的情况。此时每一点处的梯度只与当前方向有关,产生类似折线的效果,前进缓慢。而如果对梯度进行指数加权平均,这样使当前梯度不仅与当前方向有关,还与之前的方向有关,这样处理让梯度前进方向更加平滑,减少振荡,能够更快地到达最小值处。
权重W和常数项b的指数加权平均表达式如下:
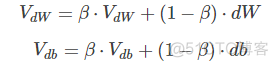
从动量的角度来看,以权重W为例,Vdw可以成速度V,dW可以看成是加速度a。指数加权平均实际上是计算当前的速度,当前速度由之前的速度和现在的加速度共同影响。而β<1,又能限制速度Vdw过大。也就是说,当前的速度是渐变的,而不是瞬变的,是动量的过程。这保证了梯度下降的平稳性和准确性,减少振荡,较快地达到最小值处。
动量梯度下降算法的过程如下:
Compute dW, db on the current mini−batch
VdW=βVdw+(1−β)dW
Vdb=βVdb+(1−β)db
W=W−αVdw, b=b−αVdb
初始时,令Vdw=0,Vdb=0。一般设置β=0.9,即指数加权平均前10天的数据,实际应用效果较好。
另外,关于偏移校正,可以不使用。因为经过10次迭代后,随着滑动平均的过程,偏移情况会逐渐消失。
补充一下,在其它文献资料中,动量梯度下降还有另外一种写法:
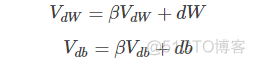
即消去了dW和db前的系数(1−β)。这样简化了表达式,但是学习因子α相当于变成了α/(1−β),表示α也受β的影响。从效果上来说,这种写法也是可以的,但是不够直观,且调参涉及到α,不够方便。所以,实际应用中,推荐第一种动量梯度下降的表达式。
7
RMSprop
RMSprop是另外一种优化梯度下降速度的算法。每次迭代训练过程中,其权重W和常数项b的更新表达式为:
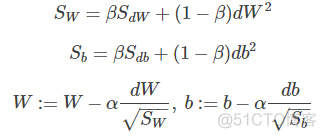
下面简单解释一下RMSprop算法的原理,仍然以下图为例,为了便于分析,令水平方向为W的方向,垂直方向为b的方向。
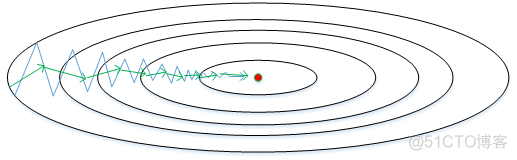

还有一点需要注意的是为了避免RMSprop算法中分母为零,通常可以在分母增加一个极小的常数ε:
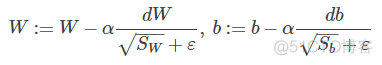
其中,ε=10^−8,或者其它较小值。
8
Adam Optimization Algorithm
Adam(Adaptive Moment Estimation)算法结合了动量梯度下降算法和RMSprop算法。其算法流程为:


实际应用中,Adam算法结合了动量梯度下降和RMSprop各自的优点,使得神经网络训练速度大大提高。
9
Learning Rate Decay
减小学习因子α也能有效提高神经网络训练速度,这种方法被称为learning rate decay。
Learning rate decay就是随着迭代次数增加,学习因子α逐渐减小。下面用图示的方式来解释这样做的好处。下图中,蓝色折线表示使用恒定的学习因子α,由于每次训练α相同,步进长度不变,在接近最优值处的振荡也大,在最优值附近较大范围内振荡,与最优值距离就比较远。绿色折线表示使用不断减小的α,随着训练次数增加,α逐渐减小,步进长度减小,使得能够在最优值处较小范围内微弱振荡,不断逼近最优值。相比较恒定的αα来说,learning rate decay更接近最优值。
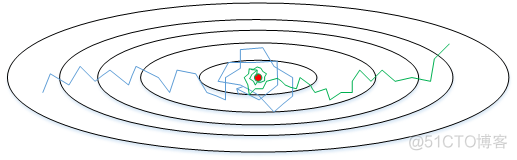
Learning rate decay中对αα可由下列公式得到:
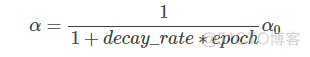
其中,deacy_rate是参数(可调),epoch是训练完所有样本的次数。随着epoch增加,α会不断变小。
除了上面计算α的公式之外,还有其它可供选择的计算公式:
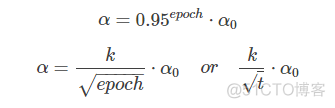
其中,k为可调参数,t为mini-bach number。
除此之外,还可以设置α为关于t的离散值,随着t增加,α呈阶梯式减小。当然,也可以根据训练情况灵活调整当前的α值,但会比较耗时间。
10
The Problem of Local Optima
在使用梯度下降算法不断减小cost function时,可能会得到局部最优解(local optima)而不是全局最优解(global optima)。之前我们对局部最优解的理解是形如碗状的凹槽,如下图左边所示。但是在神经网络中,local optima的概念发生了变化。准确地来说,大部分梯度为零的“最优点”并不是这些凹槽处,而是形如右边所示的马鞍状,称为saddle point。也就是说,梯度为零并不能保证都是convex(极小值),也有可能是concave(极大值)。特别是在神经网络中参数很多的情况下,所有参数梯度为零的点很可能都是右边所示的马鞍状的saddle point,而不是左边那样的local optimum。
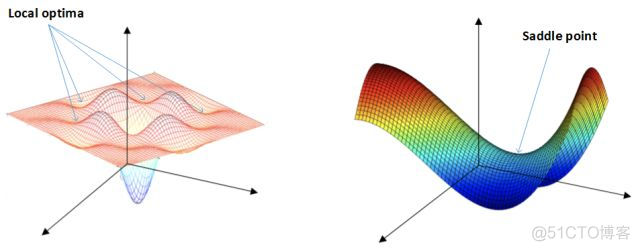
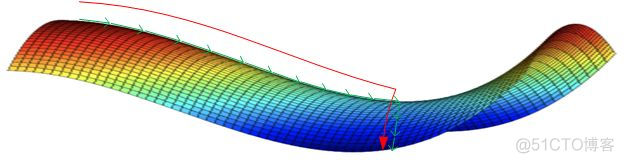
类似马鞍状的plateaus会降低神经网络学习速度。Plateaus是梯度接近于零的平缓区域,如下图所示。在plateaus上梯度很小,前进缓慢,到达saddle point需要很长时间。到达saddle point后,由于随机扰动,梯度一般能够沿着图中绿色箭头,离开saddle point,继续前进,只是在plateaus上花费了太多时间。
总的来说,关于local optima,有两点总结:
- 只要选择合理的强大的神经网络,一般不太可能陷入local optima
- Plateaus可能会使梯度下降变慢,降低学习速度
值得一提的是,上文介绍的动量梯度下降,RMSprop,Adam算法都能有效解决plateaus下降过慢的问题,大大提高神经网络的学习速度。

长按二维码扫描关注
红色石头的机器学习之路
