方差分析Analysis of Variance,ANOVA是对变量之间关系的定性分析方法,其探究的是一个因子变量对反应变量的影响。
注意:方差分析的重点不在预测,而在于分析和比较各变量之间差异。如果发现两个变量之间存在显著性差异,说明因子变量是影响反应变量的一个重要因素。
1.分类
类别 因子数量 举例 备注 单因素方差分析 1 失业率、股票收益率 多因素方差分析 >=2 施肥量和灌溉量对于粮食产量的影响 探究每个因子的影响,而不是因子整体的影响 析因方差分析 >=2 酗酒与年龄段 因子之间也存在着影响补充:
当我们只想研究多个影响因素中的一两种而非全部时,若发现一个因素对反应变量有着重要影响,但这并不能保证该因素真的对反应变量有影响。是因为可能存在另外一个与该因素相关的因素对反应变量产生了影响,该因素称为干扰因素 Confounding Factor。为避免干扰因素的影响,需加入其他变量进行控制。若加入的是因子变量,一般采取随机区组设计 Randomized Block Design,若加入的是连续变量,则该变量就是协变量,所进行的就是协方差分析 Analysis of Covariance,ANCOVA。
2.实验的影响因素
影响反应变量的因素有两大类
3.三个重要概念
以单因素为例, 说明方差分析的假设检验过程。
3.1 离差平方和
假设现在因子变量共有 $M$个水平,每个水平下试验或观测对象有$N_j$个$(j=1,2,...,M)。$令$Y_{ij}$表示第$j$个水平组别下反应变量的均值,$μ_0$代表所有反应变量的均值。若因子水平对反应变量无影响,则不同因子水平下反应变量的均值是相同的,这就是方差分析之原假设∶ $$H_0: μ_1 = μ_2 = ... = μ_M = μ_0$$ 现在我们观测到不同因子水乎下的样本数据$y_{ij}(j=1,2,...M,i=1,2,...,N_j)$,这样第$j$组的样本均值: $$\bar{y}j = \frac{y{1j}+y_{2j}+...y_{N_jj}}{N_j}=\frac{1}{N_j}\sum_{i=1}^{N_j}y_{ij}, j =1,2,...,M$$ 而全样本的平均值为:
$$\bar{y} = \frac{1}{N}\sum_{j=1}^MN_j \bar{y}j$$ 其中 $N = \sum{j=1}^MN_j \bar{y}j$ 为全样本数量。方差分析实质就是检验$\bar{y}是否与\bar{y}j相异$,现在样本观测值$y{ij}$ 与全样本均值$\bar{y}$之间的偏差可以分为两个部分: $$y{ij} - \bar{y} = y_{ij} - \bar{y}j + \bar{y}j - \bar{y}$$ 其中,$y{ij} - \bar{y}j$ 被称为组内偏差, $\bar{y}j - \bar{y}$ 称为组内偏差。将上式两边加总,就得到反映样本数据波动情况的指标——总离差平方 Total Sum of Squares TSS $$\sum{j=1}^M\sum{i=1}^{N_j}(y{ij}-\bar{y}) ^2= \sum_{j=1}^M\sum_{i=1}^{N_j}(y_{ij}-\bar{y}j)^2 + \sum{j=1}^M\sum_{i=1}^{N_j}(\bar{y}j-\bar{y}) ^2=\sum{j=1}^M\sum_{i=1}^{N_j}(y_{ij}-\bar{y}j)^2 + \sum{j=1}^MN_j(\bar{y}_j-\bar{y}) ^2$$
其中等号右边第一项为误差平方和 Error Sum of Square ESS;第二项为因子平方和 Factor Sum of Squares FSS
3.2自由度
自由度是指当以样本的统计量来估计总体的参数时,样本中能够独立或自由变动的数据的个数。比如,样本方差的计算公式为∶ $$S = \frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2$$ 其中分母$n-1$就是自由度。
总结起来,我们进行方差分析的对象共有 $N$ 个样本观测值,分布在 $M$ 个组中,第 $j$ 个组的样本量为 $N_j$。
-
$TSS$ 是衡量的是$N$个样本的总波动水平,这里所有的$N$个样本并不独立,它们满足一个约束条件(均值为$\bar{y}$): $$\sum_{j=1}^M\sum_{i=1}^{N_j}(y_{ij}-\bar{y}) = 0 $$ 故真正独立的变量只有N-1个,TSS的自由度为N-1。
-
$FSS$ 衡量的是由于因子水平变化导致的反应变量取值的波动。但是,$M$ 个因子组别的均值并不独立,$\bar{y}j, j= 1,...,M$ 满足一个约束条件∶ $$\sum{j=1}^MN_j(\bar{y}{ij}-\bar{y}) = 0 $$ 因此也丢失一个自由度,$FSS$ 的自由度是 $M-1$,其平均数组间均方差为: $$MSF=\frac{FSS}{M-1}=\frac{1}{M-1}\sum{j=1}^MN_j(\bar{y}_j-\bar{y})^2$$
-
$ESS$ 反应的是由于样本与其所处因子水平的组别均值的偏差而产生的波动,需要满足 $M$ 个约束条件 $$\sum_{i=1}^{N_j}(y_{ij}-\bar{y}j) = 0 , j=1,...,N$$ 从而失去了 $M$ 个自由度,所以 $ESS$ 的自由度是 $N-M$ ,其平均数组内均方差为∶ $$MSE=\frac{1}{N-M}\sum{j=1}^M\sum_{i=1}^{N_j}(y_{ij}-\bar{y}_j)^2$$
-
$TSS$、$FSS$ 和 $ESS$ 的自由度满足如下关系: $$N-1=(M-1)+(N一M)$$
3.3显著性检验
假设反应变量$Y_{ij}$满足条件: 根据因子水平划分的任一 $j$ 组,$Y_{ij}(i=1,2…,N_j)$为一 组独立同分布变量,且服从正态分布,即$Y_ij~N(μ_j, \sigma_0^2)$。基于这个假设,可证明出组间均方差和组内均方差的期望值满足下列公式∶ $$E(MSF)=\sigma_0^2 + \frac{1}{M-1}\sum_{j=1}{M}N_j(\mu_j-\mu_0)^2$$ $$E(MSE)=\sigma_0^2$$ 在原假设$H_0: \mu_1=\mu_1=...=\mu_M=\mu_0$, $E(MSF)=E(MSE)=\sigma_0^2$,而且方差分析的统计量: $$\varphi = \frac{MSF}{MSE}=\frac{FSS/(M-1)}{ESS/(N-M)}$$ 服从$F(M-1,N-M)$分布。
- $\varphi$ 统计量越大,说明组间均方差$MSF$与组内均方差$MSE$差异很大,且$MSF>MSE$,故$MSF$ 成为样本总波动的主要贡献,因子影响十分显著;
- $φ$ 统计量很小时,说明组间随机方差$MSE$是主要的方差来源,因子影响不显著。
我们可以查阅$F分布$的临界值表,或者计算$p值$来判断该统计量是否显著。
4. 方差分析的python实现
导入statsmodel模块
import pandas as pd import statsmodels.stats.anova as anova from statsmodels.formula.api import ols4.1 单因素方差分析
进行分析的数据如下:
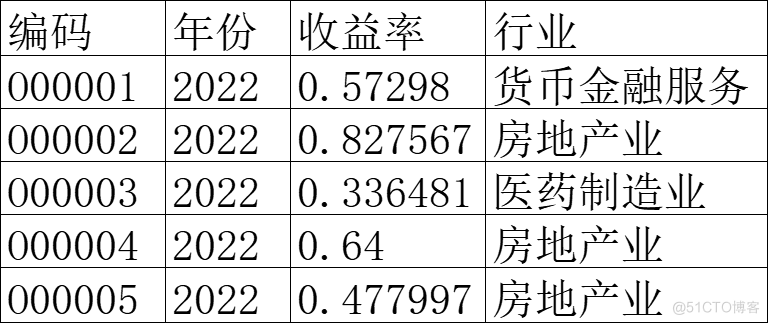
- 代码实现
- 输出结果
上述结果表明,p=4.38e一028,在0.05的显著性水平下,p值 远远小于0.05,故我们应该拒绝原假设,认为不同行业股票 2022年的年收益率是不一样的。即行业是影响股票收益率的一个重要因素。
4.2多因素方差分析
多因素方差分析的实现也很简单,我们只需要在线性回归模型里加入要研究的因素即可。现在用其来探讨婚姻状况和受教育水平对个人收入的影响,数据如下(部分):
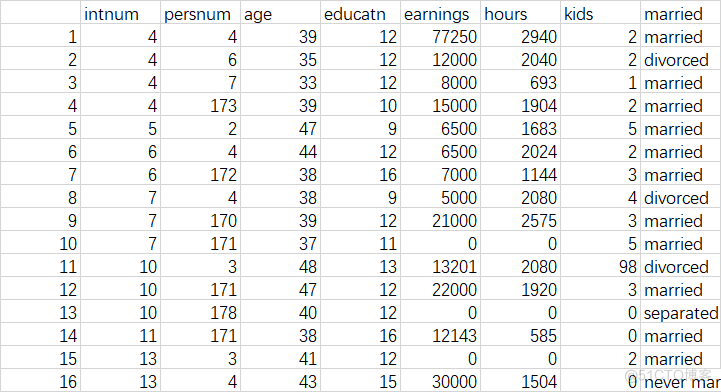
- 代码实现
- 输出结果
P值均远小与0.05,即婚姻状况和受教育水平的系数都是显著的,说明这两个因素对 收入水平有着重要的影响。
4.3析因方差分析
析因方差分析与多元素方差分析差不多,仅是多了一个因子的乘项。比如在上面的例子中,可以添加 married与educatn的乘项,以检验这两者对收入的影响是否与另一个因子的水平有关。
>>> df sum_sq ... F PR(>F) >>> C(married) 6.0 1.956487e+10 ... 15.476346 1.163717e-17 >>> C(educatn) 19.0 2.082990e+11 ... 52.032706 1.368466e-178 >>> C(married):C(educatn) 114.0 2.202005e+10 ... 0.916761 7.246151e-01 >>> Residual 4745.0 9.997547e+11 ... NaN NaN第三个系数的P值 为 0.600>0.05,即结果并不显著。所以婚姻状况和受教育水平对收入的影响并不依赖于另一者的水平。
