面试官都在问 | 比较类排序系列-堆排序

比较类排序系列-堆排序

1. 原理

堆排序是利用堆进行排序的方法。假设进行升序排序，则它的基本思想是，将待排序的序列构造成一个大顶堆，这是一个建堆的过程。此时，整个序列的最大值就是堆顶的根结点。将它与堆数组的末尾元素交换，此时末尾元素就是最大值，然后将剩余的n-1个序列，从根开始进行向下调整，重新构造成一个堆，这样就会得到n个元素中的次小值。如此反复执行交换，向下调整，便能得到一个有序序列了。如果是降序排序，则是用小顶堆，后面的过程类似。

如下图所示

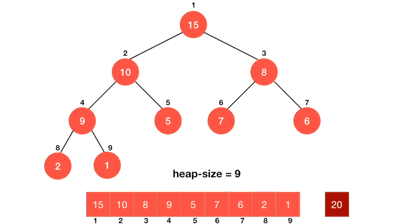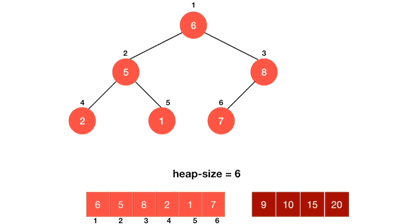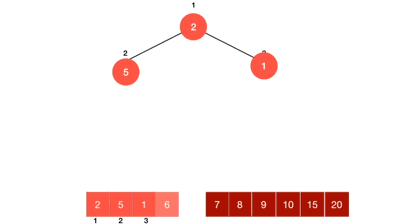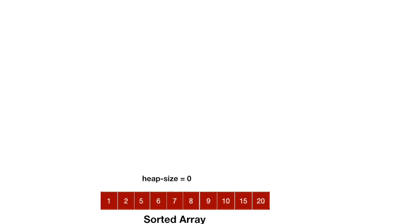
1.1向下调整

堆的向下调整主要是为了让堆中的每一个数据都满足堆的性质。如果某个数据所在的位置不满足堆的性质，则需要对其进行向下调整，给数据找到一个合适的位置。向下调整的前提条件是，当前被调整数据的子结构必须已经是一个堆。向下调整的过程如下：

从左右孩子中选择一个最大的

如果当前被调整的数据小于第一步选出的孩子，则进行交换，更新需要调整的数据位置以及孩子的位置，继续执行第一步。否则结束调整。

当更新的位置超出序列的范围则结束调整。

向下调整的过程如下所示：

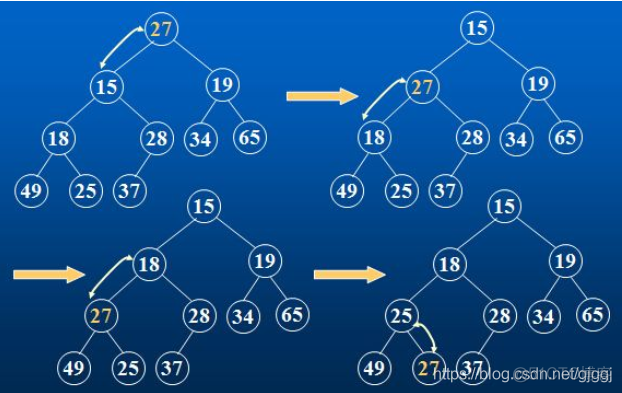
向下调整的代码如下：

void shiftDown(int* arr, int size, int parent)
{
//计算孩子的位置
int child = 2 * parent + 1;
// 从parent节点开始，一直调整到叶子节点结束
while (child < size)
{
//从两个孩子中选最大的
if (child + 1 < size && arr[child + 1] > arr[child])
++child;
//如果child 大于 parent, 向下调整，交换值
if (arr[child] > arr[parent])
{
swap(arr, child, parent);
//更新，继续向下调整
parent = child;
child = 2 * parent + 1;
}
else{
//父亲节点大于所有的孩子节点, 整体即为大堆，结束调整
break;
}
}
}public static void shiftDown(int[] arr, int sz, int parent){
//计算孩子的位置
int child = 2 * parent + 1; // left child

// 从parent节点开始，一直调整到叶子节点结束
while(child < sz){
//从两个孩子中选最大的
if(child + 1 < sz && arr[child + 1] > arr[child]){
++child;
}
if(arr[child] > arr[parent]){
//如果child 大于 parent, 向下调整，交换值
swap(arr, child, parent);
//更新，继续向下调整
parent = child;
child = 2 * parent + 1;
}
else{
//父亲节点大于所有的孩子节点, 整体即为大堆，结束调整
break;
}
}
}

1.2建堆

要对一个序列进行排序，首先应该用序列见一个堆。此时可以从最后一个非叶子节点开始，不断的执行向下调整算法，直到堆顶位置，如此，就可以建一个堆。

过程如下图所示：

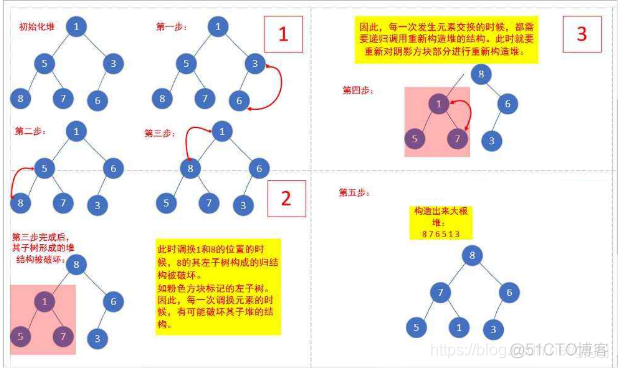
2. 代码

void swap(int* array, int i, int j)
{
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}

void heapSort(int* array, int n)
{
//建堆， 最后一个非叶子节点开始向下调整
for (int i = (n - 2) / 2; i >= 0; --i)
{
shiftDown(array, n, i);
}
//交换 《---》向下调整
// 未排序的元素个数
int end = n - 1;
while (end > 0)
{
swap(array, 0, end);
//给剩余元素向下调整
shiftDown(array, end, 0);
--end;
}
}public static void swap(int[] arr, int i, int j){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}

public static void heapSort(int[] arr){
int len = arr.length;
//建堆， 最后一个非叶子节点开始向下调整
for(int i = (len - 2) / 2; i >= 0; --i){
shiftDown(arr, i, len);
}
//交换 《---》向下调整
// 未排序的元素个数
int end = len - 1;
while(end > 0){
swap(arr, 0, end);
shiftDown(arr, 0, end);
--end;
}
}

3. 时间空间复杂度

3.1 时间复杂度

堆排序中过程中需要不断的进行向下调整的操作，向下调整的操作时间复杂度为O(logn), 对于每一个数据，都需要进行一次向下调整，故时间复杂度为O(nlogn)。

3.2 空间复杂度

堆排序过程中只需要创建常数个局部变量，故空间复杂度为O(1)。

总结