EXISTS 谓词的用法
支撑 SQL 和关系数据库的基础理论主要有两个:一个是数学领域的集合论,另一个是作为现代逻辑学标准体系的谓词逻辑(predicate logic),准确地说是“一阶谓词逻辑”。EXISTS 是为了实现谓词逻辑中“量化”(quantification)这一强大功能而被引入 SQL 的。
1\. 什么是谓词?
1.1 概述
SQL 的保留字中,有很多都被归为谓词一类。例如,“= 、< 、>”等比较谓词,以及 BETWEEN 、LIKE 、IN 、IS NULL 等。当然,我们说的谓词和主语/谓语中的谓语,以及英语中的动词是不一样的。
实际上,谓词是一种特殊的函数,返回值是真值。前面提到的每个谓词,返回值都是 true 、 false 或者 unknown (一般的谓词逻辑里没有 unknown ,但是 SQL 采用的是三值逻辑,因此具有三种真值)。谓词逻辑提供谓词是为了判断命题(可以理解成陈述句)的真假,而在关系数据库里,表中的一行数据可以看作是一个命题。
Tbl_A:
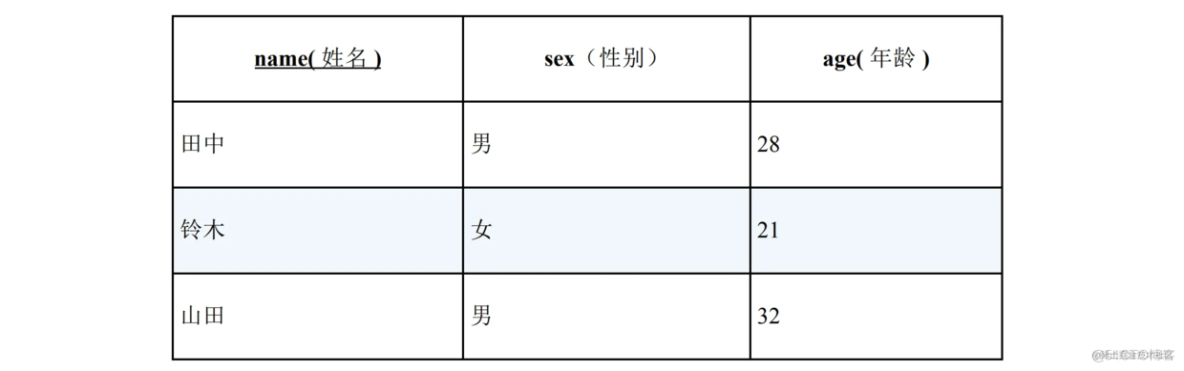
例如,这张表里第一行数据就可以认为表示这样一个命题:田中性别是男,而且年龄是 28 岁。
表常常被认为是行的集合,但从谓词逻辑的观点看,也可以认为是命题的集合(也就是描述每一行记录陈述句的集合)。
也就是说,我们平时使用的 WHERE 子句,其实也可以看成是由多个谓词组合而成的新谓词。只有能让 WHERE 子句的返回值为真的命题,才能从表(命题的集合)中查询到。
1.2 实体的阶层
同样是谓词,但是与 = 、BETWEEN 等相比,EXISTS 的用法还是大不相同的。概括来说,区别在于“谓词的参数可以取什么值”。“x = y ”或“x BETWEEN y ”等谓词可以取的参数是像“13”或者“本田”这样的单一值,我们称之为标量值。而 EXISTS 可以取的参数究竟是什么呢?从下面这条 SQL 语句来看,EXISTS 的参数不像是单一值。
SELECT idFROM Foo F
WHERE EXISTS (SELECT * FROM Bar B WHERE F.id=B.id );
可以看出参数是行数据的集合。之所以这么说,是因为无论子查询中选择什么样的列,对于 EXISTS 来说都是一样的。
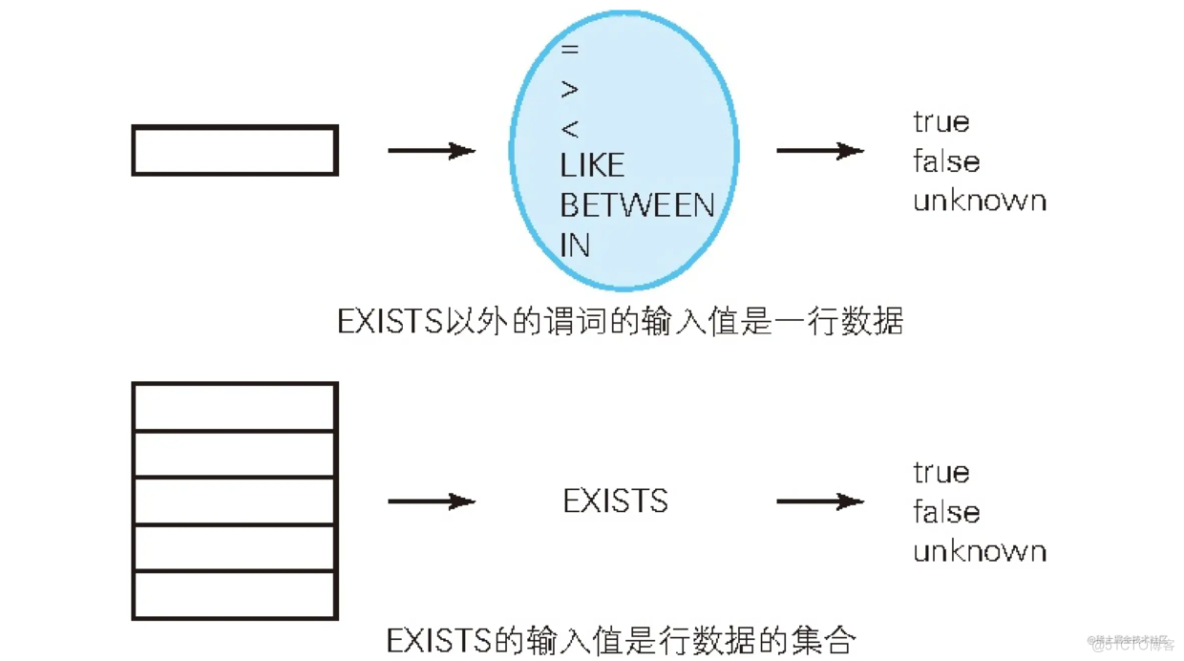
从上面的图表我们可以知道,EXISTS 的特殊性在于输入值的阶数(输出值和其他谓词一样,都是真值)。谓词逻辑中,根据输入值的阶数对谓词进行分类。= 或者 BETWEEEN 等输入值为一行的谓词叫作“一阶谓词”,而像 EXISTS 这样输入值为行的集合的谓词叫作“二阶谓词”。阶(order)是用来区分集合或谓词的阶数的概念。
类似Java中的“高阶函数”这一概念。它指的是不以一般的原子性的值为参数,而以函数为参数的函数。这里说的“阶”和谓词逻辑里的“阶”是一个意思(“阶”的概念原本就源于集合论和谓词逻辑)。EXISTS 因接受的参数是集合这样的一阶实体而被称为二阶谓词,但是谓词也是函数的一种,因此我们也可以说 EXISTS 是高阶函数。
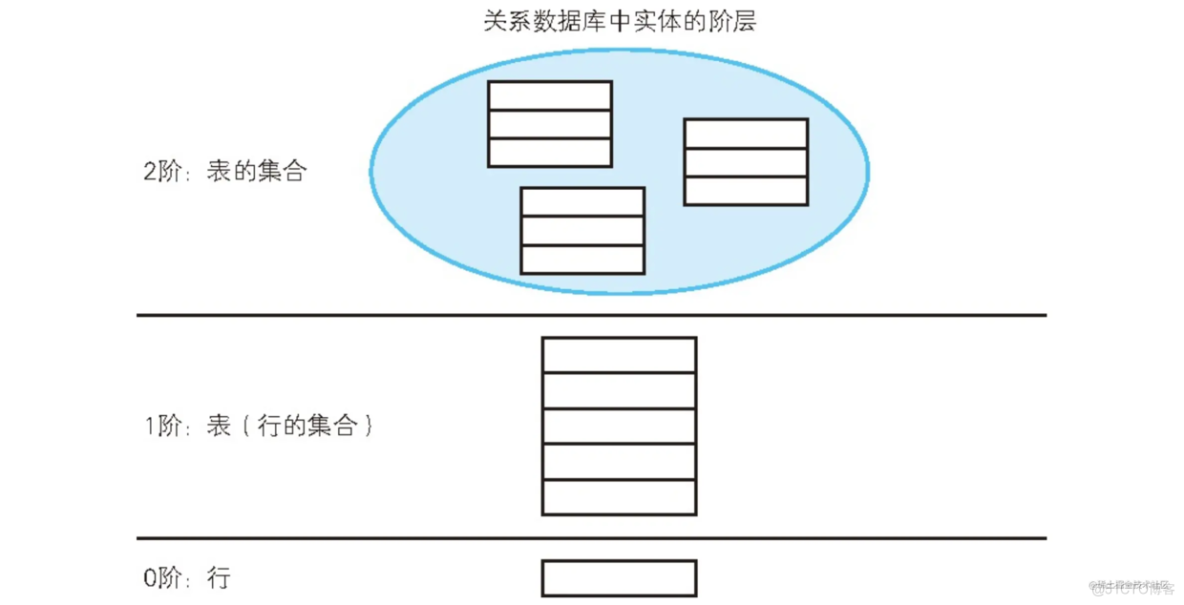
SQL 中采用的是狭义的“一阶谓词逻辑”,这是因为 SQL 里的 EXISTS 谓词最高只能接受一阶的实体作为参数。如果想要支持二阶、三阶等更高阶的实体,SQL 必须提供相应的支持。理论上这也是可以做到的 ,只是目前还没有实现。
1.3 全称量化和存在量化
谓词逻辑中有量词(限量词、数量词)这类特殊的谓词。我们可以用它们来表达一些这样的命题:“所有的 x 都满足条件 P”或者“存在(至少一个)满足条件 P 的 x ”。前者称为“全称量词”,后者称为“存在量词”,分别记作 ∀、∃。
也许大家已经明白了,SQL 中的 EXISTS 谓词实现了谓词逻辑中的存在量词。然而遗憾的是,对于另一个全称量词,SQL 却并没有予以实现。
但是没有全称量词并不算是 SQL 的致命缺陷。因为全称量词和存在量词只要定义了一个,另一个就可以被推导出来。具体可以参考这个等价改写的规则(德·摩根定律):
- ∀ x P x = ¬ ∃ x ¬P :所有的 x 都满足条件 P = 不存在不满足条件 P 的 x 。
- ∃ x P x = ¬ ∀ x ¬Px :存在 x 满足条件 P = 并非所有的 x 都不满足条件 P 。
2\. 查询表中“不”存在的数据
2.1 小试牛刀
Meetings:
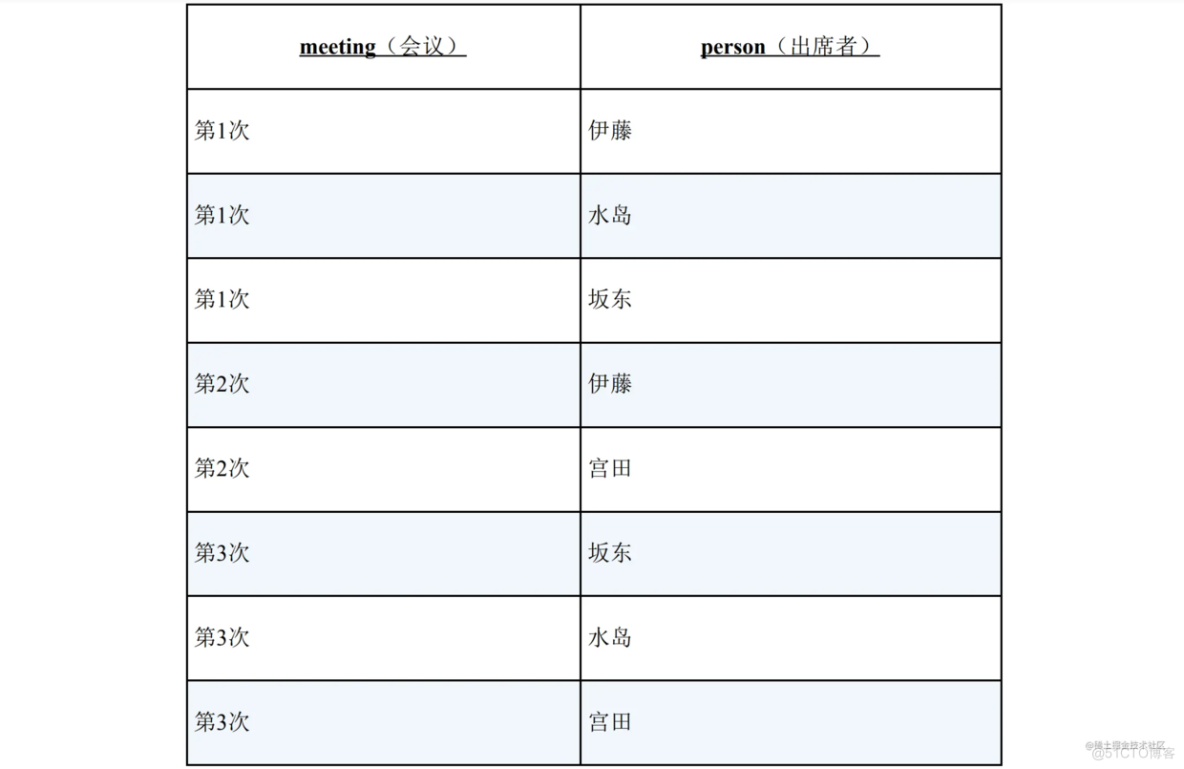
现在需要查询的是没有参加某次会议的人,下面给出了议缺席者列表:
meeting person---------- --------
第 1 次 宫田
第 2 次 坂东
第 2 次 水岛
第 3 次 伊藤
首先可以想到查询出所有人都参加了所有会议的情况:
SELECT DISTINCT M1.meeting, M2.personFROM Meetings M1 INNER JOIN Meetings M2;
然后我们从这张表中减掉实际参会者的集合,即表 Meetings 中存在的组合即可。
-- 求出缺席者的SQL 语句(1):存在量化的应用SELECT DISTINCT
M1.meeting,
M2.person
FROM
Meetings M1
INNER JOIN Meetings M2
WHERE
NOT EXISTS ( SELECT * FROM Meetings M3 WHERE M1.meeting = M3.meeting AND M2.person = M3.person );---- 求出缺席者的 SQL 语句(2):使用差集运算
SELECT
M1.meeting,
M2.person
FROM
Meetings M1, Meetings M2
EXCEPT
SELECT
meeting,
person
FROM
Meetings;
通过以上两条 SQL 语句的比较我们可以明白,NOT EXISTS 直接具备了差集运算的功能。
2.2 “肯定与双重否定”之间的转换
TestScores:
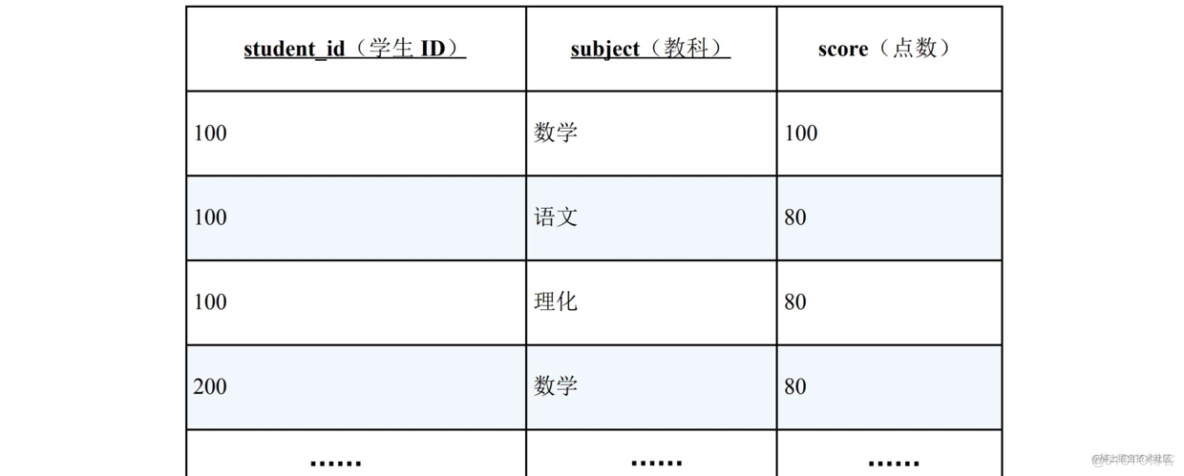
上图是一张存储了学生考试成绩的表,这里只展示出了部分数据。
先来看一个简单的问题:请查询出“所有科目分数都在 50 分以上的学生”,解法是,将查询条件“所有科目分数都在 50 分以上”转换成它的双重 否定“没有一个科目分数不满 50 分”,然后用 NOT EXISTS 来表示转换后的命题。
SELECT DISTINCTstudent_id
FROM
TestScores TS1
WHERE
NOT EXISTS ( SELECT * FROM TestScores TS2 WHERE TS2.student_id = TS1.student_id AND TS2.score < 50 );
现在需要查询出满足“该学生的所有行数据中,数学分数在 80 分以上;语文分数在 50 分以上”的学生。
SELECTstudent_id
FROM
TestScores TS1
WHERE
SUBJECT IN ( '数学', '语文' ) AND
NOT EXISTS (
SELECT
*
FROM
TestScores TS2
WHERE
TS2.student_id = TS1.student_id
AND 1 =
CASE WHEN SUBJECT = '数学' AND score < 80 THEN 1
WHEN SUBJECT = '语文' AND score < 50 THEN 1
ELSE 0
END
);
GROUP BY student_id
HAVING COUNT(*) = 2;
首先,数学和语文之外的科目不在我们考虑范围之内,所以通过 IN 条件进行一下过滤。然后,通过子查询来描述“数学 80 分以上,语文 50 分以上”这个条件。再者,学生必须两门科目都有分数才行,所以我们可以加上用于判断行数的 HAVING 子句来实现。
2.3 “集合与谓词”哪个更强大?
EXISTS 和 HAVING 有一个地方很像,即都是以集合而不是个体为单位来操作数据。实际上,两者在很多情况下都是可以互换的,用其中一个写出的查询语句,大多时候也可以用另一个来写。
Projects:
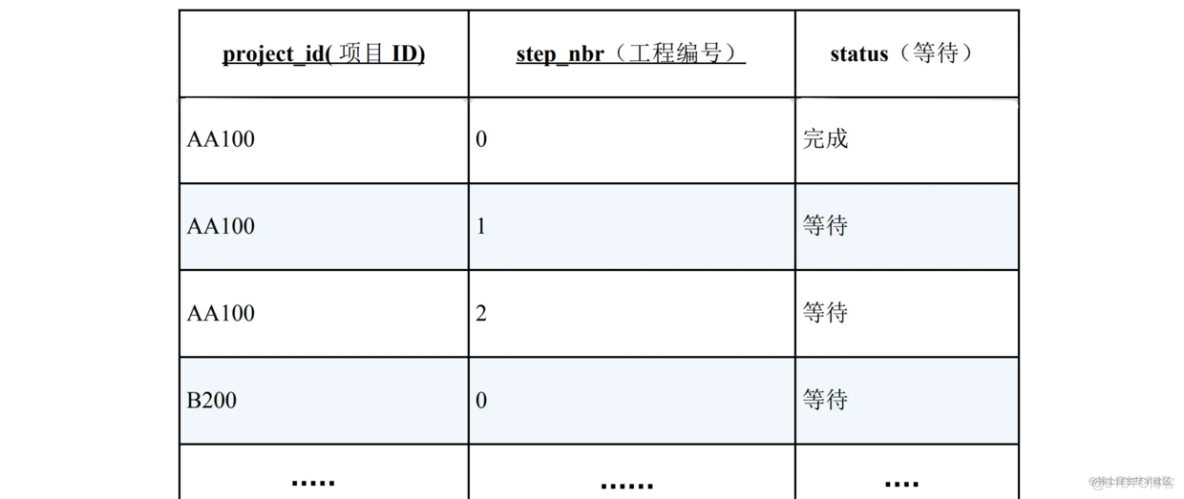
这张表的主键是“项目 ID,工程编号”。工程编号从 0 开始,我们不妨认为 0 号是需求分析,1 号是基本设计……虽然这张表中部分数据的工程编号最大只到 2,但是有可能也会有 3 及以后的编号。已经完成的工程其状态列的是“完成”,等待上一个工程完成的工程其状态列的是“等待”。
这里的问题是,从这张表中查询出哪些项目已经完成到了 (也就是说1及之前的工程都处于完成状态,1之后的工程都处于等待状态)工程 1。
-- 查询完成到了工程1 的项目:面向集合的解法SELECT
project_id
FROM
Projects
GROUP BY
project_id
HAVING
COUNT(*) = SUM(
CASE WHEN step_nbr <= 1 AND STATUS = '完成' THEN 1
WHEN step_nbr > 1 AND STATUS = '等待' THEN 1
ELSE 0
END);
这里针对每个项目,将工程编号为1以下且状态为“完成”的行数,和工程编号大于1且状态为“等待”的行数加在一起,如果和等于该项目数据的总行数,则该项目符合查询条件。
-- 查询完成到了工程1 的项目:谓词逻辑的解法SELECT
*
FROM
Projects P1
WHERE
NOT EXISTS (
SELECT status
FROM
Projects P2
WHERE
P1.project_id = P2.project_id AND
STATUS <> CASE WHEN step_nbr <= 1 THEN '完成'
ELSE '等待'
END
);
虽然两者都能表达全称量化,但是与 HAVING 相比,使用了双重否定的 NOT EXISTS 代码看起来不是那么容易理解,这是它的缺点。
但是这种写法也有优点:
这里也可以把 NOT EXISTS 改写成 ALL 谓词的话,就不需要双重否定了。
-- 查找已经完成到工程1 的项目:使用ALL谓词解答SELECT
*
FROM
Projects P1
WHERE
'○' = ALL (
SELECT
CASE WHEN step_nbr <= 1 AND STATUS = '完成' THEN '○'
WHEN step_nbr > 1 AND STATUS = '等待' THEN '○'
ELSE '×'
END
FROM
Projects P2
WHERE
P1.project_id = P2.project_id
);
如果对满足条件的行标记“○”,对不满足条件的行标记“×”,那么我们要查找的其实就是“所有行都被标记了○的项目”。这也是特征函数的一种应用。这种解法没有使用双重否定句,使用的是肯定句,理解起来很轻松。
这条查询语句有一个好处是查询结果中还包含集合的具体内容,但是因为需要对所有的行标记○或者×,所以性能没有使用 NOT EXISTS时好。
2.4 对列进行量化
ArrayTbl:
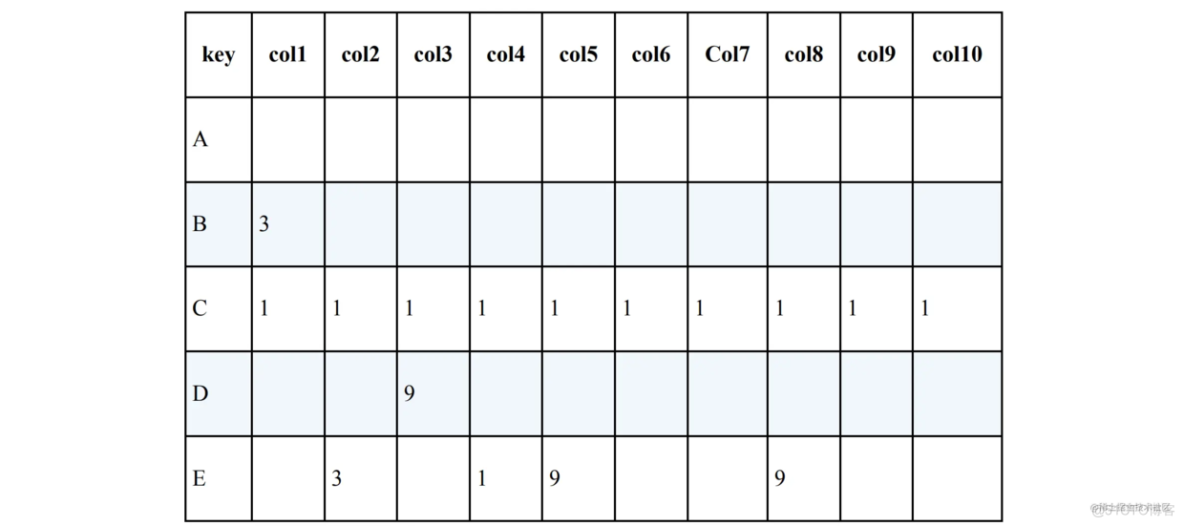
这里的问题是查询全是 1 的行。当然可以使用下面这种常规的解法:
--“列方向”的全称量化:不优雅的解答SELECT *
FROM ArrayTbl
WHERE col1 = 1
AND col2 = 1
·
·
·
AND col10 = 1;
SQL 语言其实还准备了一个谓词,帮助我们进行“列方向”的量化。
--“列方向”的全称量化:优雅的解答SELECT *
FROM ArrayTbl
WHERE 1 = ALL (col1, col2, col3, col4, col5, col6, col7, col8, col9, col10);
此段代码在 PostgreSQL 中运行时会报错。要想成功运行,需将代码最后一行括号内的字符改为“values(col1),(col2),(col3),(col4),(col5),(col6),(col7),(col8),(col9),(col10)”。
反过来,如果想表达“至少有一个9”这样的存在量化命题,可以使用ALL的反义谓词 ANY。
-- 列方向的存在量化(1)SELECT *
FROM ArrayTbl
WHERE 9 = ANY (col1, col2, col3, col4, col5, col6, col7, col8, col9, col10);
或者也可以使用 IN 谓词代替 ANY 。
-- 列方向的存在量化(2)SELECT *
FROM ArrayTbl
WHERE 9 IN (col1, col2, col3, col4, col5, col6, col7, col8, col9, col10);
我们一般都像 col1 IN (1, 2, 3) 这样来使用 IN 谓词,左边是列名,右边是值的列表,但是其实这种写法也是被允许的。但是需要注意的是,如果左边不是具体值而是 NULL ,这种写法就不行了。这种情况下,我们可以使用 COALESCE 函数。
-- 查询全是NULL 的行:正确的解法SELECT *
FROM ArrayTbl
WHERE COALESCE(col1, col2, col3, col4, col5, col6, col7, col8, col9, col10) IS NULL
3\. 问题
3.1 求质数
Numbers:
这是一张存储了 1 ~ 100 的所有自然数的表Numbers,现在需要做的就是求出这1 ~ 100 中的质数。
-- 解答:用NOT EXISTS 表达全称量化SELECT
num AS prime
FROM
Numbers Dividend
WHERE
num > 1 AND
NOT EXISTS (
SELECT
*
FROM
Numbers Divisor
WHERE
Divisor.num <= Dividend.num / 2 AND
Divisor.num <> 1 AND
MOD ( Dividend.num, Divisor.num ) = 0
)
ORDER BY
prime;
“不能被1和它自身以外的所有自然数整除” 换而言之就是 “除了1和它自身以外,不存在能整除它的自然数”。因为约数不包含自身,所以约数必定小于等于自身值的一半,因此我们可以通过 Divisor.num <= Dividend.num/2 这样的条件缩小查找范围。此外,因为连接条件可以用到“num”列的索引,所以性能也比较好。
