计算阶乘

1.背景知识

阶乘是基斯顿·卡曼（Christian Kramp，1760～1826）于 1808 年发明的运算符号。一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，通俗的讲也就是按顺序从1乘到n，所得的那个数就是n的阶乘。0的阶乘为1，自然数n的阶乘写作n!。即：0！= 11！= 12！= 2 × 1！= 2 × 13！= 3 × 2！= 3 × 2 × 1n！= n × (n - 1)！= n × (n - 1) × (n - 2) ×...× 2 × 1

输入一个整数n，求其阶乘n!

1.1双阶乘

双阶乘用“m！！”表示。

当 m 是自然数时，表示不超过 m 且与 m 有相同奇偶性的所有正整数的乘积。如：

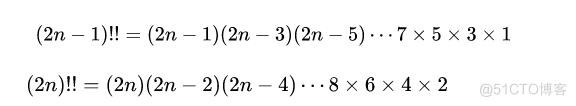
当 m 是负奇数时，表示绝对值小于它的绝对值的所有负奇数的绝对值积的倒数。

当 m 是负偶数时，m！！不存在。

自然数双阶乘比的极限

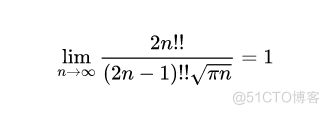
阶乘的逼近函数公式

对于正整数

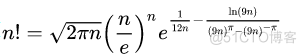
2.如何解题

• 用input函数请用户输入一个整数，因为负数无阶乘，需使用户输入的数为自然数
• 根据阶乘的特点：n！= n × (n - 1)！= n × (n - 1) × (n - 2) ×...× 2 × 1，可用for循环、递归等方法求解
• 需考虑特殊情况：0！= 1

3.解题方法

方法一：for循环

a = int(input('请输入一个自然数:'))
result = 1
if a < 0:
print('负数没有阶乘')
elif a == 0:
print('0的阶乘为1')
else:
for i in range(1, a + 1):
result *= i
print(f"{a}的阶乘为{result}")

第1行： 定义变量a，用input函数使用户输入数字，int函数将其转换为整型

第2行： 创建一个存储阶乘运算结果的变量result，变量初始值为1

第3-10行： 用if...elif...else语句对用户输入的数值进行判断。若用户输入的数值小于0，输出“负数没有阶乘”；若用户输入的数值等于0，输出“0的阶乘为1”；否则用for循环遍历1 至 a 的整数，在每轮循环中，result都会与循环变量 i 相乘并将乘积结果再赋值给result，当for循环结束时，result的值就是自然数n阶乘的运算结果，最后用print函数输出阶乘结果。

方法二： 递归法

def factorial(n):
assert n >= 0, "请输入自然数"
if n == 0:
return 1
return n * factorial(n - 1)


a = int(input('请输入一个自然数:'))
print(factorial(a))

第1行： 定义函数factorial，传入参数n

第2行： 用assert断言函数限定参数n大于或等于0，若大于或等于0，执行后面的代码，否则报错“AssertionError: 请输入自然数！

第3-5行： 设定递归的结束条件，当 n 为 0时，返回值为1，否则返回值为n * factorial(n - 1)

第8行： 定义变量a，用input函数使用户输入数字，int函数将其转换为整型

第9行： 为参数n赋值为a，用print函数打印计算结果

方法三： reduce()函数

from functools import reduce


def factorial(n):
assert n >= 0, "请输入自然数"
if n == 0:
return 1
return reduce(lambda x, y: x * y, range(1, n + 1))


a = int(input('请输入一个自然数:'))
print(factorial(a))

第1行： 从functools模块中导入reduce()函数

第4行： 定义函数factorial，传入参数n

第5行： 用assert断言函数限定参数n大于或等于0，若大于或等于0，执行后面的代码，否则报错“AssertionError: 请输入自然数！”

第6-7行： 设定递归的结束条件，当 n 为 0时，返回值为1

第8行： 调用reduce函数，使用lambda 表达式输出前n项的积

第11行： 定义变量a，用input函数使用户输入数字，int函数将其转换为整型

第12行： 为参数n赋值为a，用print函数打印计算结果

educe() 函数

reduce() 函数是functools模块中的一个函数，其作用是对参数序列中元素进行累积。

语法：reduce(function, iterable[, initializer])

参数说明：function：是包含两个参数的函数iterable ：可迭代对象initializer ：初始参数

def prod(x, y):
return x + y
print(reduce(prod, [1, 2, 3, 4, 5])) # 15

函数prod有两个参数x和y，迭代对象是[1,2,3,4,5]，计算过程为((((1+2)+3)+4)+5)，在函数function的两个参数中，左边的参数x是被累积的值，而右边的参数y是依次从序列中获取的值。可以使用lambda表达式来简化代码：

print(reduce(lambda x, y: x + y, [1, 2, 3, 4, 5])) # 15

lambda 表达式

Lambda 函数是Python中的匿名函数，也就是没有具体名称的函数，通常是在需要一个函数，但是又不想费神去命名一个函数的场合下使用 。

lambda 表达式的两个要点：

• lambda 表达式必须使用 lambda 关键字定义。
  在 lambda 关键字之后、冒号左边为参数列表，可不带参数，也可有多个参数。若有多个参数，则参数间用逗号隔开，冒号右边为 lambda 表达式的返回值。

方法四： factorial()函数

import math
a = int(input('请输入一个自然数:'))
result = math.factorial(a)
print(f"{a}的阶乘为{result}")

第1行： 导入模块math

第2行： 定义变量a，用input函数使用户输入数字，int函数将其转换为整型

第3行： 创建变量result，调用math模块中的factorial函数，传入参数a

第4行： print函数输出结果