LeetCode 第232场周赛 2021年3月14日
大家好,我叫亓官劼(qí guān jié )
文章目录
- LeetCode 第232场周赛 2021年3月14日
- 5701. 仅执行一次字符串交换能否使两个字符串相等
- 题目
- 解题思路
- 算法实现一 C++
- 算法实现二 Python
- 算法实现三 python
- 5702. 找出星型图的中心节点
- 解题思路
- 算法实现一 python
- 算法实现二 C++
- 5703. 最大平均通过率
- 解题思路
- 算法实现 C++
- 算法实现 Python(超时了)
- 5704. 好子数组的最大分数
- 算法实现
5701. 仅执行一次字符串交换能否使两个字符串相等
题目
给你长度相等的两个字符串 s1 和 s2 。一次 字符串交换 操作的步骤如下:选出某个字符串中的两个下标(不必不同),并交换这两个下标所对应的字符。
如果对 其中一个字符串 执行 最多一次字符串交换 就可以使两个字符串相等,返回 true ;否则,返回 false 。
示例 1:
输入:s1 = "bank", s2 = "kanb"输出:true
解释:例如,交换 s2 中的第一个和最后一个字符可以得到 "bank"
示例 2:
输入:s1 = "attack", s2 = "defend"输出:false
解释:一次字符串交换无法使两个字符串相等
示例 3:
输入:s1 = "kelb", s2 = "kelb"输出:true
解释:两个字符串已经相等,所以不需要进行字符串交换
示例 4:
输入:s1 = "abcd", s2 = "dcba"输出:false
提示:
- 1 <= s1.length, s2.length <= 100
- s1.length == s2.length
- s1 和s2 仅由小写英文字母组成
解题思路
模拟交换S1中的各个元素,如果交换后的S1和S2相同,则return true 否则换回,继续下一次模拟,如果全部模拟完后还没返回,则false
算法实现一 C++
class Solution {public:
bool areAlmostEqual(string s1, string s2) {
int len1 = s1.length(), len2 = s2.length();
if(len1 != len2)
return false;
for(int i = 0 ; i < len1; i++){
for(int j = i; j < len1; j++){
swap(s1[i],s1[j]);
if(s1 == s2)
return true;
swap(s1[i],s1[j]);
}
}
return false;
}
};
算法实现二 Python
正在转python中,目前实现方法可能不是太好,在改进中
class Solution:def areAlmostEqual(self, s1: str, s2: str) -> bool:
if len(s1) != len(s2):
return False
s1 = list(s1)
s2 = list(s2)
i = 0
while i < len(s1):
j = i
while j < len(s1):
s1[i],s1[j] = s1[j], s1[i]
if s1 == s2:
return True
s1[i],s1[j] = s1[j], s1[i]
j += 1
i += 1
return False
算法实现三 python
class Solution:def areAlmostEqual(self, s1: str, s2: str) -> bool:
# 存S1和S2不同的字符
res = []
if len(s1) != len(s2):
return False
for i in range(len(s1)):
if s1[i] != s2[i]:
res.append([s1[i],s2[i]])
# 如果res中为空,即全部相同,则可以
if len(res) == 0:
return True
# res中的个数不为2时,一定不可以通过一次交换后相同
if len(res) != 2:
return False
# 交换后相同
if res[0][1] == res[1][0] and res[0][0] == res[1][1]:
return True
return False
5702. 找出星型图的中心节点
有一个无向的 星型 图,由 n 个编号从 1 到 n 的节点组成。星型图有一个 中心 节点,并且恰有 n - 1 条边将中心节点与其他每个节点连接起来。
给你一个二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示在节点 ui 和 vi 之间存在一条边。请你找出并返回 edges 所表示星型图的中心节点。
示例 1:
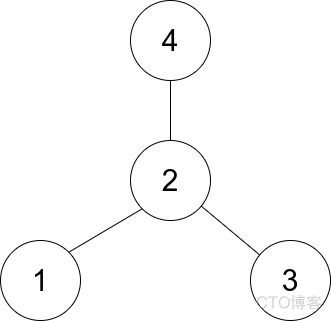
输出:2
解释:如上图所示,节点 2 与其他每个节点都相连,所以节点 2 是中心节点。
示例 2:
输入:edges = [[1,2],[5,1],[1,3],[1,4]]输出:1
提示:
- 3 <= n <= 105
- edges.length == n - 1
- edges[i].length == 2
- 1 <= ui, vi <= n
- ui != vi
- 题目数据给出的edges 表示一个有效的星型图
解题思路
这里给的是无向图,保证存在中心节点。那我们只需要找到在所有边集中,出现len次的点即可。
算法实现一 python
class Solution:def findCenter(self, edges: List[List[int]]) -> int:
len1 = len(edges)
mp = {}
for edge in edges:
for item in edge:
if item not in mp.keys():
mp[item] = 1
else:
mp[item] += 1
if mp[item] == len1:
return item
return 0
算法实现二 C++
class Solution {public:
int findCenter(vector<vector<int>>& edges) {
unordered_map<int,int> hash;
for(int i = 0; i < edges.size(); i++){
for(int j = 0 ; j < edges[i].size(); j++){
hash[edges[i][j]]++;
if (hash[edges[i][j]] == edges.size())
return edges[i][j];
}
}
return 0;
}
};
5703. 最大平均通过率
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] = [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学生可以通过考试。
给你一个整数 extraStudents ,表示额外有 extraStudents 个聪明的学生,他们 一定 能通过任何班级的期末考。你需要给这 extraStudents 个学生每人都安排一个班级,使得 所有 班级的 平均 通过率 最大 。
一个班级的 通过率 等于这个班级通过考试的学生人数除以这个班级的总人数。平均通过率 是所有班级的通过率之和除以班级数目。
请你返回在安排这 extraStudents 个学生去对应班级后的 最大 平均通过率。与标准答案误差范围在 10-5 以内的结果都会视为正确结果。
示例 1:
输入:classes = [[1,2],[3,5],[2,2]], extraStudents = 2输出:0.78333
解释:你可以将额外的两个学生都安排到第一个班级,平均通过率为 (3/4 + 3/5 + 2/2) / 3 = 0.78333 。
示例 2:
输入:classes = [[2,4],[3,9],[4,5],[2,10]], extraStudents = 4输出:0.53485
提示:
- 1 <= classes.length <= 105
- classes[i].length == 2
- 1 <= passi <= totali <= 105
- 1 <= extraStudents <= 105
解题思路
多路归并问题,采用贪心方法。这里每个班级为一个待归并集合,采用优先队列存储节点 ,按每次增加一个人,班级所增加的通过率的大小进行排序。每次取优先队列的队头,即加一个人,所增加的增长率最大的。然后更新优先队列。
对于每个班级来说,总人数total,通过人数pass,则增加一个人所增加的通过率为:(pass+1)/(total+1) - pass/total化简后即:(total - pass) / (total * (total+1))
算法实现 C++
class Solution {public:
double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {
struct Node {
double v; // 增加一个人,增加的通过率
int total,pass; // 通过人数,总数
bool operator< (const Node& t) const {
return v < t.v;
}
};
priority_queue<Node> heap;
double sum = 0;
for (auto& c: classes) {
int total = c[1], pass = c[0];
sum += (double) pass / total;
heap.push({(total - pass) / (total * (total + 1.0)), total, pass});
}
// 贪心,每次取优先队列的队头,即加一个人,所增加的增长率最大的。然后更新优先队列
while (extraStudents -- ) {
auto t = heap.top();
heap.pop();
sum += t.v;
int total = t.total + 1, pass = t.pass + 1;
heap.push({(total - pass) / (total * (total + 1.0)), total, pass});
}
return sum / classes.size();
}
};
算法实现 Python(超时了)
在python中没找到大根堆的容器,使用sort和max都超时了
from heapq import *class Solution:
def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:
heap = []
res = 0
for item in classes:
# 增加一个人所增加的通过率:(total - pass) / (total * (total+1))
heap.append([item[0],item[1],(item[1]-item[0])/(item[1]*(item[1]+1))])
res = res + item[0]/item[1]
heap.sort(key = lambda item:item[2],reverse=True)
while extraStudents:
res = res + heap[0][2]
heap.append([heap[0][0]+1,heap[0][1]+1,(heap[0][1]-heap[0][0])/((heap[0][1]+1)*(heap[0][1]+2))])
heap.remove(heap[0])
heap.sort(key = lambda item:item[2],reverse=True)
extraStudents -= 1
return res / len(classes)
5704. 好子数组的最大分数
给你一个整数数组 nums **(下标从 0 开始)**和一个整数 k 。
一个子数组 (i, j) 的 分数 定义为 min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1) 。一个 好 子数组的两个端点下标需要满足 i <= k <= j 。
请你返回 好 子数组的最大可能 分数 。
示例 1:
输入:nums = [1,4,3,7,4,5], k = 3输出:15
解释:最优子数组的左右端点下标是 (1, 5) ,分数为 min(4,3,7,4,5) * (5-1+1) = 3 * 5 = 15 。
示例 2:
输入:nums = [5,5,4,5,4,1,1,1], k = 0输出:20
解释:最优子数组的左右端点下标是 (0, 4) ,分数为 min(5,5,4,5,4) * (4-0+1) = 4 * 5 = 20 。
提示:
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 2 * 104
- 0 <= k < nums.length
算法实现
这题暴力超时了,这里附一份Y总的代码,供大家参考。
class Solution {public:
int maximumScore(vector<int>& nums, int k) {
int n = nums.size();
vector<int> h(n + 2, -1), l(n + 2), r(n + 2), stk(n + 2);
for (int i = 1; i <= n; i ++ ) h[i] = nums[i - 1];
int tt = 0;
stk[0] = 0;
for (int i = 1; i <= n; i ++ ) {
while (h[stk[tt]] >= h[i]) tt -- ;
l[i] = stk[tt];
stk[ ++ tt] = i;
}
tt = 0, stk[0] = n + 1;
for (int i = n; i; i -- ) {
while (h[stk[tt]] >= h[i]) tt -- ;
r[i] = stk[tt];
stk[ ++ tt] = i;
}
k ++ ;
int res = 0;
for (int i = 1; i <= n; i ++ )
if (l[i] < k && r[i] > k)
res = max(res, (r[i] - l[i] - 1) * h[i]);
return res;
}
};
