设T=(V,E,W)是一个无圈且连通的无向图(也称为无根树),每条边带有正整数的权,我们称T为树网(treenetwork),其中v,E分别表示结点与边的集合,W表示各边长度的集合,并设T有n个结点。
路径:树网中任何两结点a,b都存在唯一的一条简单路径,用d(a,b)表示以a,b为端点的路径的长度,它是该路径上各边长度之和。我们称d(a,b)为a,b两结点问的距离。
一点v到一条路径p的距离为该点与p上的最近的结点的距离:
d(v,P)=min{d(v,u),u为路径P上的结点)。
树网的直径:树网中最长的路径称为树网的直径。对于给定的树网T,直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距ECC(F):树网T中距路径F最远的结点到路径F的距离,即 ECC(F)=max{d(v,F),V∈V}。
任务:对于给定的树网T=(V,E,W)和非负整数s,求一个路径F,它是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过s(可以等于s),使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E,W)的核(Core)。必要时,F可以退化为某个结点。一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
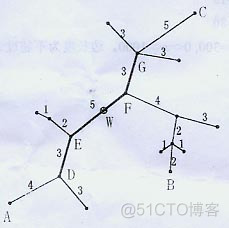
下面的图给出了树网的一个实例。图中,A-B与A-C是两条直径,长度均为20。点W是树网的中心,EF边的长度为5。如果指定s=11,则树网的核为路径DEFG(也可以取为路径DEF),偏心距为8。如果指定s=O(或s=1、s=2),则树网的核为结点F,偏心距为12。
40%的数据满足:5<=n<=15
70%的数据满足:5<=n<=80
100%的数据满足:5<=n<=300,0<=s<=1000。边长度为不超过1000的正整数。
O(n^3) 暴力找出所有直径
O(tn^2) 暴力找出所有直径上的一段路径,其长度不超过s
O(t’n^2) 暴力枚举每条直接对每个点的距离
using namespace std;
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
#define
typedef long long ll;
typedef unsigned long long ull;
ll mul(ll a,ll b){return (a*b)%F;}
ll add(ll a,ll b){return (a+b)%F;}
ll sub(ll a,ll b){return (a-b+llabs(a-b)/F*F+F)%F;}
void upd(ll &a,ll b){a=(a%F+b%F)%F;}
int read()
{
int x=0,f=1; char ch=getchar();
while(!isdigit(ch)) {if (ch=='-') f=-1; ch=getchar();}
while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar();}
return x*f;
}
#define
int f[MAXN][MAXN];
bool b[MAXN][MAXN]={0};
int t;
vector<pi> v,v2;
int main()
{
// freopen("D.in","r",stdin);
// freopen(".out","w",stdout);
MEMI(f)
int S,n;
cin>>n>>S;
For(i,n-1) {
int a,b;
cin>>a>>b;
f[a][b]=f[b][a]=read();
}For(i,n) f[i][i]=0;
For(k,n) For(i,n) For(j,n)
f[i][j]=min((ll)f[i][j],(ll)f[i][k]+f[k][j]);
int l=0;
For(i,n) For(j,n) l=max(l,f[i][j]);
t=0;
For(i,n) Fork(j,i,n) if (f[i][j]==l) {
v.pb(mp(i,j));
}
t=v.size();
Rep(k,t) {
For(i,n) {
if (f[v[k].fi][i]+f[i][v[k].se]==l)
Fork(j,i,n) {
if (f[v[k].fi][j]+f[j][v[k].se]==l)
if (f[i][j]<=S&&!b[i][j]) {
b[i][j]=1;
v2.pb(mp(i,j));
}
}
}
}
int ans=INF;
t=v2.size();
Rep(k,t) {
int x=v2[k].fi,y=v2[k].se;
int p1=0;
For(i,n) {
if (f[x][i]+f[i][y]!=f[x][y]) {
int p=INF;
For(j,n) {
if (f[x][j]+f[j][y]==f[x][y]) p=min(f[j][i],p);
}
p1=max(p1,p);
}
}
ans=min(ans,p1);
}
cout<<ans<<endl;
return 0;
}
