python中dot函数运算过程总结

目录

• 基本简介
• 1. 向量内积
• 2. 矩阵乘法运算
• 2.1如下单个数的dot函数运算所示：
• 2.2如下一维数组的dot函数运算所示：
• 2.3如下二维数组的dot函数运算所示：
• 2.4如下二维数组与三维数组的dot函数运算：
• 2.5如下多维数组的dot函数运算所示：
• 总结

本文结合其他博主的一些介绍总结了dot函数运算过程

基本简介

dot函数为numpy库下的一个函数，主要用于矩阵的乘法运算，其中包括：向量内积、多维矩阵乘法和矩阵与向量的乘法。

1. 向量内积

向量其实是一维的矩阵，两个向量进行内积运算时，需要保证两个向量包含的元素个数是相同的。

例1：

import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2, 3, 4, 5, 6, 7, 8])
result = np.dot(x, y)
print(result)

输出结果：

168

计算过程就是将向量中对应元素相乘，再相加所得。即普通的向量乘法运算。

2. 矩阵乘法运算

注意：

1.数组的运算是元素级的，数组相乘的结果是各对应元素的积组成的数组，而对于矩阵而言，需要求的是点积

2.两个矩阵(x, y)如果可以进行乘法运算，需要满足以下条件：

   x为 m×n 阶矩阵，y为 n×p 阶矩阵，

   则相乘的结果 result 为 m×p 阶矩阵。例子如下

例2：

import numpy as np
x = np.array([[1, 2, 3],
[3, 4, 4]])
y = np.array([[0, 1, 1, 1],
[1, 2, 0, 1],
[0, 0, 2, 1]])
result = np.dot(x, y)
print(result)
print("x阶数：" + str(x.shape))
print("y阶数：" + str(y.shape))
print("result阶数：" + str(result.shape))

结果为：

[[ 2 5 7 6]

[ 4 11 11 11]]

x阶数：(2, 3)

y阶数：(3, 4)

result阶数：(2, 4)

下面我们来分析一下一维数组到多维数组之间的运算过程

2.1如下单个数的dot函数运算所示：

np.dot(5,8)40

2.2如下一维数组的dot函数运算所示：

#如果arr1和arr2都是一维数组，那么它返回的就是向量的内积

arr1=np.array([2,3])
arr2=np.array([4,5])
np.dot(arr1,arr2)
#23

如图所示： 

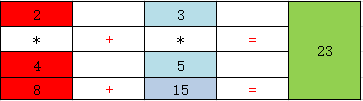
2.3如下二维数组的dot函数运算所示：

#如果arr5 和arr6都是二维数组，那么它返回的是矩阵乘法

arr5=np.array([[2,3],[4,5]])
arr6=np.array([[6,7],[8,9]])
np.dot(arr5,arr6)
"""
array([36,4],
          [64,73])
"""

运算过程如下所示： 

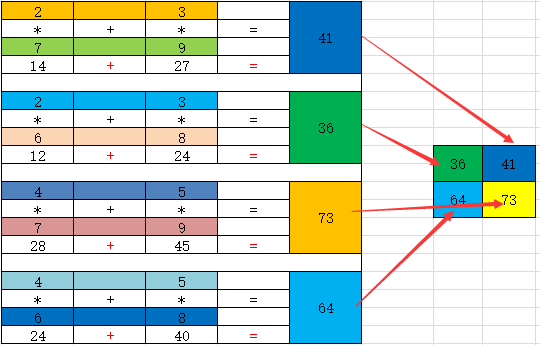
2.4如下二维数组与三维数组的dot函数运算：

#arr7二维数组与arr8三维数组的dot函数矩阵运算

arr7=np.array([[2,3,4],[5,6,7]])
arr8=np.array([[0,1,2],[3,4,5],[6,7,8]])
np.dot(arr7,arr8)
"""
array([33,42,51],[60,78,96])
"""

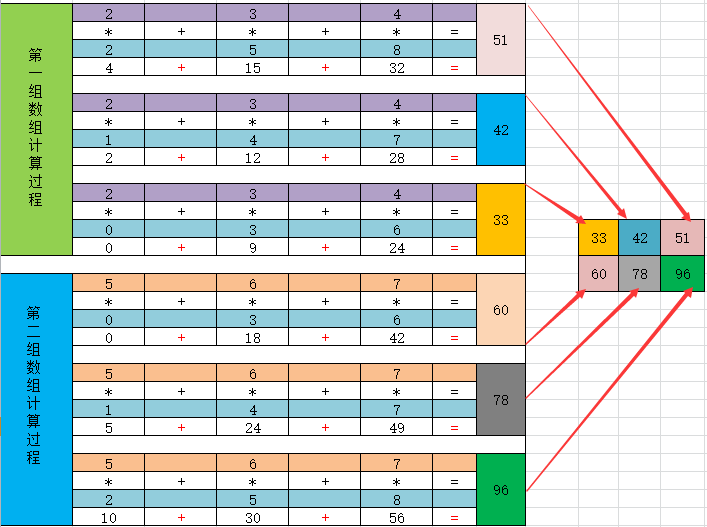
2.5如下多维数组的dot函数运算所示：

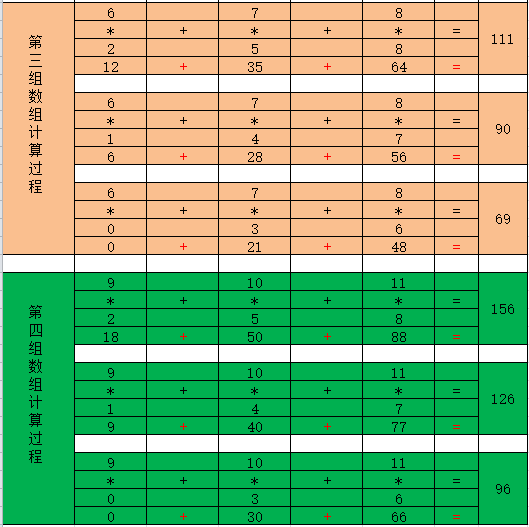
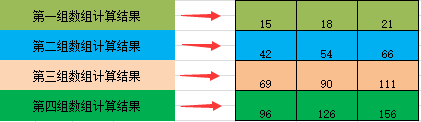
#多维数组的dot函数矩阵运算
arr12=np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])
arr13=np.array([[0,1,2],[3,4,5],[6,7,8]])
np.dot(arr12,arr13)
"""
array([15,18,21],
        [42,54,66],
        [69,90,111],
        [96,126,156])
"""

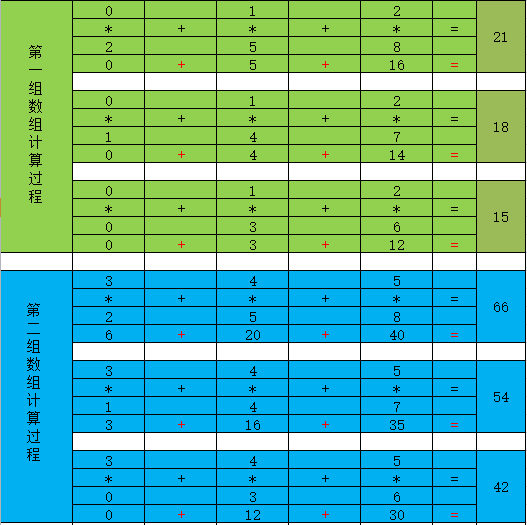
注意：

dot()函数可以通过NumPy库调用，也可以由数组实例对象进行调用。例如：a.dot(b) 与 np.dot(a,b)效果相同。但矩阵积计算不遵循交换律,np.dot(a,b) 和 np.dot(b,a) 得到的结果是不一样的。

总结

到此这篇关于python中dot函数运算的文章就介绍到这了,更多相关python dot函数内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！