C++中的数组、链表与哈希表

目录

• 数组和链表
• 数组
• 链表
• 什么是链表？
• 链表的操作
• 双向链表（list）
• list的成员函数
• 哈希表
• 什么是哈希表？
• 哈希碰撞
• 哈希表应用场景
• 构建哈希表
• 哈希表基本使用
• Leetcode对应题目
• 前缀和
• 差分数组
• 滑动窗口
• 二分查找

数组和链表

C++的数组和链表分别是什么？分别有什么种类？它们都有什么特性？针对这些特征，使用情形是什么？

数组

什么是数组？

一个数组就像是一个变量，它可以存储一组值，但是所有值都是相同的数据类型。 

一个int数组定义：int hours [6]

该数组类型为int型，即存储元素是整数。

该数组的名称是hours，方括号内为数组的大小，它表示数组可以容纳的元素或值的数量，必须是一个常量整数，其值大于0.（也可以是命名常数）

初始化数组：int hours[6] = { 1, 2, 3, 4, 5, 6}.

访问数组元素

数组的元素可以根据下标作为单独的变量进行访问和使用，C++中的下标编号从0开始，数组中最后一个元素的下标比数组中元素的总数少1.

如果采用全局定义的方式定义一个包含数值的数组，则默认情况下，所有元素初始化为0.但是，如果定义的是局部变量，则没有默认的初始值。 

上面hours数组的每个元素在被下标访问时都可以用做int变量赋值：hours[0] = 20

可变长的动态数组：vector

vector是顺序容器的一种，是可变长的动态数组。所以vector具备数组的性质：在vector容器中，根据下标随机访问某个元素的时间是常数，在尾部添加一个元素的时间大多数情况也是常数。

但是，在中间插入或删除元素，需要移动多个元素，速度较慢，平均花费时间和容器中的元素个数成正比。

Vector基本用法

成员函数作用vector()无参构造函数，将容器初始化为空vector(int n)将容器初始化为有n个元素vector(int n, const T &val)假定元素类型为T，将容器初始化为有n个元素，每个元素的值都是valvector(iterator first, iterator last)first，last可以是其他容器的迭代器。一般来说，本构造函数的初始化结果就是将vector容器的内容变成与其他容器上的区间[first，last）一致void clear()删除所有元素bool empty()判断容器是否为空void pop_back()删除容器末尾的元素void push_back(const T &val)将val添加到容器末尾int size()返回容器中元素的个数T & front()返回容器中第一个元素的引用T & back()返回容器中最后一个元素的引用iterator insert(iterator i, const T &val)将val插入迭代器i指向的位置，返回iiterator insert(iterator i, iterator first, iterator last)将其他容器上的区间[first，last)中的元素插入迭代器i指向的位置iterator erase(iterator i)删除迭代器i指向的元素，返回值是被删元素后面的元素的迭代器iterator erase(iterator first, iterator last)删除容器中的区间[first, last)void swap(vector < T > &v)将容器自身的内容和另一个同类型的容器v互换

#include <vector>
using namespace std;
int main(){
	int a[5] = {1, 2, 3, 4, 5}
	vector <int> v(a, a+5); //将数组a的内容放入v
	cout << v.end() - v.begin() << endl; //两个迭代器相减，输出：5
	v.insert(v.begin()+2, 13); // 在begin()+2 位置插入13， v变为：1，2,13,3，4,5
	v.eraser(v.begin()+2); // 删除位于begin()+2 位置上的元素，v变为：1,2,3,4，5
	vector <int> v2(4, 100); // v2有4个元素，都是100
	v2.insert(v2.begin(), v.begin() + 1, v.begin() +3); // 将v的一段插入v2开头，v2： 2,3,100,100,100,100
	v.erase(v.begin()+1, v.begin()+3); // 删除v上的区间，即[2,3),v:1,4,5
	// 遍历
	int sum = 0;
	// 迭代器遍历
	for(std::vector<int>::iterator it = v.begin(); it !=v.end(); it++){
		sum += *it;
	}
	//索引遍历(不适用list)
	for(int i = 0; i < v.size(); i++){
		sum += v[i];
	}
}

链表

什么是链表？

链表是由一系列连接在一起的结点构成，其中的每一个结点都是一个数据结构。

链表的结点是动态分配、使用和删除的。相对于数组来说，链表可以容易地扩大或缩小，无需知道链表有多少个结点；相对于矢量（vector）来说，链表插入或删除结点的速度更快，因为要将值插入vector的中间，需要将插入点后的所有元素都向后移动一个位置，而链表插入结点，其他结点不必移动。

链表的结构：链表中的每个结点都包含一个或多个保存数据的成员，和一个后继指针指向链表的下一个结点。单节点组成如下：

在c++中表示链表，需要有一个表示链表中单个结点的数据类型。

struct ListNode
{
	double value;  // 数据
	ListNode *next; // 指向另一个相同类型结点的指针
}

非空链表的第一个结点成为链表的头。要访问链表中的结点，需要有一个指向链表头的指针。从链表头开始，可以按照存储在每个结点中的后继指针访问链表中的其余结点。最后一个结点的后继指针被设置为nullptr。

已经声明一个数据类型来表示结点后，可定义一个初始为空的链表。即定义一个用作链表头的指针并将其初始化为nullptr：ListNode *head = nullptr;

创建一个链表。其中包含一个结点，存储值为12.5

head = new ListNode; //分配新结点
head->value = 12.5; 
head->next = nullptr; // 链表的结尾

在单向链表中，头head指向最先节点的前一个，尾end指向最后节点，新加入一个点，即加在未加入结尾时的链表的结尾的后一个。

  1 - 5 - 2 - 9 - 8
h                 e
这是原来的链表(h=head,e=end) 
新读入3,要把3加入链表的最后面
那么就要加在8的后面  
  1 - 5 - 2 - 9 - 8 -   3
h                 e   e->next
                       tmp
这样子end->next就指向3,也就是tmp
因为end是指向point类型的指针
新加入3后我们发现end不在结尾上,那么我们要调整
即end=tmp
  1 - 5 - 2 - 9 - 8 - 3
h                     e

创建一个新结点，在其中存储13.5的值，并将其作为链表中的第二个结点。

ListNode *secondPtr = new ListNode;
secondPtr->value = 13.5;
secondPtr->next = nullptr;
head->next = secondPtr; //第一个结点指向第二个

链表的操作

1.使用构造函数初始化结点 ——结点在创建时可初始化

struct ListNode
{
	double value;
	ListNode *next;
	//构造函数
	ListNode(double value1; ListNode *next1 = nullptr){
		value = value1;
		next = next1;
	}
};

2.创建链表——读取文件中的值并将每个新读取的值添加到已经累积的值链表的开头

ListNode *numberList = nullptr;
double number;
while(numberFile >> number){
	// 创建一个结点以保存该数字
	numberList = new ListNode(number, numberList);
};

3.遍历链表——从链表头开始，涉及整个链表，并在每个结点上执行一些处理操作

ListNode *ptr = numberList; // 一个指针ptr指向链表的开头
while(ptr != nullptr){
		cout << ptr->value; // 打印结点的值；
		ptr = ptr->next; // 移动到下一个结点
};

双向链表（list）

list是顺序容器的一种，是一个双向链表。双向链表的每个元素中都有一个指针指向后一个元素，一个指针指向前一个元素。

在list容器中，在已经定位到要增删元素的位置的情况下，增删元素能在常数时间内完成。如图2所示，在ai和ai+1之间插入一个元素，只需要修改ai和ai+1中的指针即可。

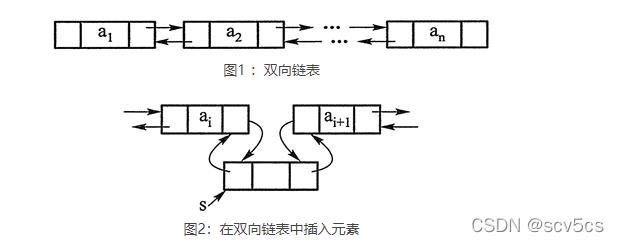
但是list容器不支持根据下标随机存取元素。

list的成员函数

list的构造函数和许多成员函数的用法都与vector类似，初此之外，还有独特接口。（以下省略与vector相同的接口）

void push_front(const T &val); //在头部添加元素
void pop_front(); //删除头部元素
void sort(); //排序
void remove(const T &val); // 删除值为val的所有元素
void remove_if(bool (*pred)(const T &val)); // 删除满足条件的所有元素
void unique(); // 删除连续的重复元素（只保留第一个）
void merge(list < T> &x); // 在自身有序的前提下，与另一个有序链表x合并，并保持有序。
void splice(iterator i, list < T> &x, iterator i); //在位置i前插入链表x中的一个结点（剪切操作）
void splice(iterator i, list < T> &x, iterator first, iterator last); // 在位置i前插入链表x中的区间[first, last)，并在链表x中删除该区间。链表自身和链表x可以是同一个链表，只要i不在[first，last)中即可

哈希表

什么是哈希表？

散列图（Hash table，也叫哈希表），是根据关键码值（Key value）而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

给定表M，存在函数f(key),对任意给定的关键字值key，代入函数后若能得到包含该关键词的记录在表中的地址，则称表M为哈希（Hash）表，函数f(key)为哈希(Hash)函数。

数据的哈希地址 = f(关键字key的值)

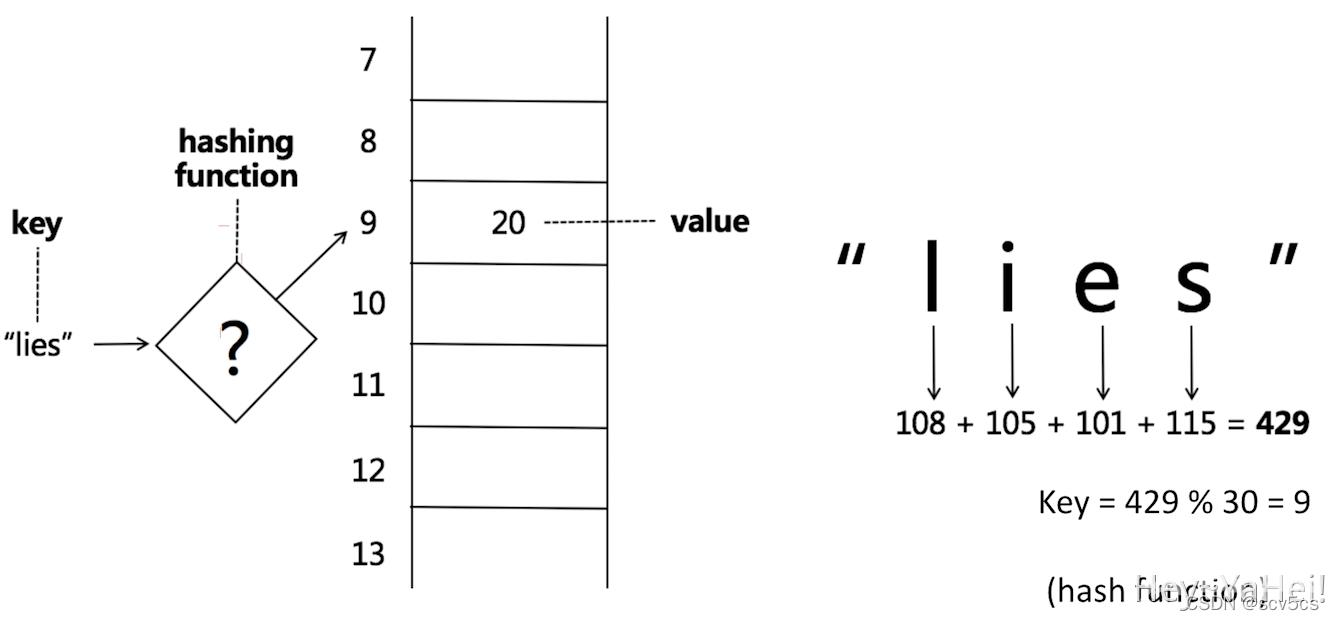
通俗解释：哈希表是一种数据结构，可以直接根据给定的key值计算出目标位置。在工程中，哈希表结构通常采用数组实现。

普通列表仅能通过下标来获取目标位置的值，而哈希表可以根据给定的key计算得到目标位置的值。

列表查找中，二分查找算法，复杂度为O(log2n),只能用于有序列表；普通无序列表只能采用遍历查找，复杂度为O(n);而用哈希函数实现的哈希表，对任意元素查找速度始终是常数级别，即O(1).

哈希碰撞

一个哈希值会对应多种值。即不同的key值，哈希函数结果一样，都指向同一个value地址，出现重复。

对于哈希表而言，冲突只能尽可能地少，无法完全避免。通常用顺序表存一堆链表来解决这个问题：

哈希表应用场景

哈希表的优点是可以通过关键值计算直接获取目标位置，对于海量数据的精确查找有显著速度提升，理论上即使有无限的数据量，一个良好的哈希表依旧可以保持O(1)的查找速度。

在工程上，经常用于通过名称制定配置信息、通过关键词传递参数、建立对象与对象的映射关系等。总而言之，所有使用键值对的地方，都用到了哈希表思想。

构建哈希表

在构建哈希表时，最重要的是哈希函数的设计。常用的哈希函数的构造方法有6种：直接定址法、数字分析法、平方取中法、折叠法、除留余数法和随机数法。

1.直接定址法：哈希函数为一次函数，即一下两种形式：

 H(key) = key /  H(key) =  a * key + b

2.数字分析法：如果关键字由多位字符或数字组成，可以考虑抽取其中的2位或者多位作为该关键字对应的哈希地址，在取法上尽量选择变化较多的位，避免冲突发生。

3.平方取中：对关键字做平方操作，取中间的几位作为哈希地址。适合关键字位数较短

4.折叠法：将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位）作为哈希地址。此方法适合关键字位数较多的情况。

5.除留余数法：若一直整个哈希表的最大长度m，可以取一个不大于m的数p，然后对该关键字key做取余运算：H(key) = key % p。此方法中，p的取值非常重要，由经验得p可以为不大于m的质数或不包含小于20的质因数的合数。

6.随机数法：去关键字的一个随机函数值作为它的哈希地址，即H(key) = random(key).适合关键字长度不等的情况。 

set和map都可以由哈希表和二叉搜索树实现。

在C++STL中，哈希表对应的容器是unordered_map，访查插删时间复杂度为O(1)，但内部是无序的，额外空间复杂度高出许多。map对应的数据结构是红黑树，访查插删时间复杂度为O(logn),内部是有序的。对于需要高效率查询的情况，使用unordered_map容器，对内存大小比较敏感或者数据要求有序的情况，可以用map容器。

哈希表基本使用

unordered_map的用法和map大同小异：

#include <iostream>
#include <unordered_map>
#include <string>
int main(int argc, char **argv){
	std::unordered_map<int, std::string> map;
	map.insert(std::make_pair(1, "Scale");
	map.insert(std::make_pair(2, "java");
	map.insert(std::make_pair(3, "python");
	map.insert(std::make_pair(6, "Erlang");
	map.insert(std::make_pair(13,"Haskell");
	
	std::unordered_map<int, std::string>::iterator it;
	if((it = map.find(6)) != map.end()){
		std::cout << it->second << std::endl;
	}
	return 0;
}

Leetcode对应题目

前缀和

前缀和技巧：对应题目：303、304、560（ 用到哈希表 ）

前缀和主要适用场景是：原始数组不会被修改的情况下，频繁查询某个区间的累加和。

差分数组

差分数组：对应题目：370、1109、1094

差分数组主要适用场景：频繁对原始数组某个区间的元素进行增减

滑动窗口

滑动窗口：对应题目：76、567、438、3 

和子数组/子字符串相关的题目，很可能要考察滑动窗口，往这方面思考就行了

滑动窗口算法思路:

我们在字符串S中使用左右双指针，初始化left = right = 0， 把索引左闭右开区间[left, right)称为一个窗口；先不断地增加right指针，扩大窗口[left, right)，直到窗口中的字符串符合要求（包含了T中的所有字符）;（寻找可行解）此时，停止增加right，转而不断增加left指针缩小窗口[left， right)，直到窗口中的字符串不再符合要求（不包含T中的所有字符了）。同时，每增加left，更新一次。（优化可行解，寻找最优解）重复2、3步，直到right到达字符串s的尽头。

左右指针轮流前进，窗口大小增增减减，窗口不断右滑。

关键问题：

• 1.当right扩大窗口，即加入字符时，需要更新哪些数据?
• 2.什么条件下，窗口应该暂停扩大，开始移动left缩小窗口？
• 3.当移动left缩小窗口，移出字符时，应该更新哪些数据？
• 4.我们要的结果应该在扩大窗口还是缩小窗口时更新？

二分查找

二分查找对应题目：704、34、875、1011

分析二分查找的一个技巧是:不要出现else，而是把所有情况用else if写清楚，这样可以清楚地展示所有细节。 另外需要声明一下，计算mid时需要防止溢出，left + (right - left) / 2 和 (left + right) / 2 结果相同，但是有效防止了 left和right太大直接相加导致溢出。

什么问题可以运用二分搜索算法技巧？

首先，你要从题目中抽象出一个自变量x，一个关于x的函数f(x)，以及一个目标值target。

同时，f(x)必须是在x上的单调函数；题目是让你计算满足约束条件f(x) == target时的x的值。

具体来说，想要用二分搜索算法解决问题，分为以下几步：

• 1.确定x， f(x)， target分别是什么，并写出函数f的代码；
• 2.找到x的取值范围作为二分搜索的搜索区间，初始化left和right变量
• 3.根据题目要求，确定应该使用搜索左侧还是右侧的二分搜索算法，写出解法代码 

以上为个人经验，希望能给大家一个参考，也希望大家多多支持自由互联。